Общее уравнение кривой второго порядка

Мы говорили, что алгебраическая кривая второго порядка определяется алгебраическим уравнением второго степени относительно х и у. В общем виде такое уравнение записывается так

А х ² + В ху + С у ² +D x + E y + F = 0, (6)

причем А² + В² + С² ¹ 0 (т.е. одновременно числа А, В, С в ноль не обращаются). Слагаемые А х ², В ху, С у ² называются старшими членами уравнения, число

d =

называется дискриминантом этого уравнения. Уравнение (6) называется общим уравнением кривой второго порядка.

Для рассмотренных ранее кривых имеем:

Эллипс: Þ А = , В = 0, С = 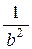, D = Е = 0, F = –1,

d = . 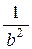>0;

окружность х ² + у ² = а ² Þ А = С = 1, В = D = Е = 0, F = – а ², d = 1>0;

Гипербола: Þ А = , В = 0, С = – 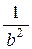, D = Е = 0, F = –1,

d = – . 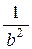< 0.

Парабола: у ² = 2 рх Þ А = В = 0, С=1, D = –2 р, Е = F = 0, d = 0,

х ² = 2 ру Þ А = 1В = С= D = 0, Е = –2 р, F = 0, d = 0.

Кривые, заданные уравнением (6), называются центральными кривыми, если d¹0. Если d> 0, то кривая эллиптического типа, если d<0, то кривая гиперболического типа. Кривые, для которых d = 0 являются кривыми параболического типа.

Доказано, что линия второго порядка в любой декартовой системе координат задается алгебраическим уравнением второго порядка. Только в одной системе уравнение имеет сложный вид (например, (6)), а в другой – более простой, например, (5). Поэтому удобно рассматривать такую систему координат, в которой изучаемая кривая записывается наиболее простым (например, каноническим) уравнением. Переход от одной системы координат, в которой кривая задается уравнением вида (6) к другой, где ее уравнение имеет более простой вид, называется преобразованием координат.

Рассмотрим основные виды преобразований координат.

I. Преобразование переноса координатных осей (с сохранением направления). Пусть в исходной системе координат ХОУ точка М имеет координаты (х, у), а в новой системе координат ХО¢У она имеет координаты (х ¢, у ¢). Из чертежа видно, что координаты точки М в разных системах связаны соотношениями

(7), или (8).

Формулы (7) и (8) называются формулами преобразования координат.

II. Преобразование поворота координатных осей на угол a. Если в исходной системе координат ХОУ точка М имеет координаты (х, у), а в новой системе координат ХО¢У она имеет координаты (х ¢, у ¢). То связь между этими координатами выражается формулами

, (9)

или

С помощью преобразования координат уравнение (6) можно привести к одному из следующих канонических уравнений.

1) – эллипс,

2) – гипербола,

3) у ² = 2 рх, х ² = 2 ру – парабола

4) а ² х ² – b ² y ² = 0 – пара пересекающихся прямых (рис. а)

5) y ² – a ² = 0 – пара параллельных прямых (рис. б)

6) x ² – a ² = 0 – пара параллельных прямых (рис. в)

7) y ² = 0 – совпадающие прямые (ось ОХ)

8) x ² = 0 – совпадающие прямые (ось ОУ)

9) а ² х ² + b ² y ² = 0 – точка (0, 0)

10) 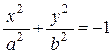мнимый эллипс

11) y ² + a ² = 0– пара мнимых прямых

12) x ² + a ² = 0 пара мнимых прямых.

Каждое из этих уравнений является уравнением линии второго порядка. Линии, определяемые уравнениями 4 – 12, называют вырожденными кривыми второго порядка.

Рассмотрим примеры преобразования общего уравнения кривой к каноническому виду.

1) 9 х ² + 4 у ² – 54 х + 8 у + 49 = 0 Þ (9 х ² – 54 х) + (4 у ²+ 8 у) + 49 = 0 Þ

9(х ² – 6 х + 9) + 4(у ² + 2 у + 1) – 81 – 4 + 49 = 0 Þ 9(х –3)² + 4(у + 1) = 36, Þ

.

Положим х ¢ = х – 3, у ¢ = у + 1, получим каноническое уравнение эллипса . Равенства х ¢ = х – 3, у ¢ = у + 1 определяют преобразование переноса системы координат в точку (3, –1). Построив старую и новую системы координат, нетрудно изобразить данный эллипс.

2) 3 у ² +4 х – 12 у +8 = 0. Преобразуем:

(3 у ²– 12 у)+ 4 х +8 = 0

3(у ² – 4 у +4) ­– 12 + 4 х +8 = 0

3(у – 2)² + 4(х –1) = 0

(у – 2)² = – (х – 1).

Положим х ¢ = х – 1, у ¢ = у – 2, получим уравнение параболы у ¢² = – х ¢. Выбранная замена соответствует переносу системы координат в точку О¢(1,2).

Чтобы построить параболу, достаточно определить дополнительно хотя бы одну ее точку (либо относительно новой, либо относительно старой системы координат) положим х ¢ = –3, получим у ¢ = ± 2, т.е. нашли целых две точки: (–3, 2) и (–3, –2) в новой системе координат.

По этим точкам и вершине, которая находится в новом начале координат О¢, можно изобразить параболу.

3) 4 х ² – у ² + 8 х + 6 у – 5 = 0 Þ

4 х ²+ 8 х – у ²+ 6 у – 5 = 0,

4(х ²+ 2 х +1) –(у ²– 6 у +9)–4 +9 – 5 = 0,

4(х +1)² –(у +3)² = 0.

Замена х ¢ = х +1, у ¢ = у – 3 приводит к уравнению 4 х ¢² – у ¢² = 0 – это пара пересекающихся прямых в системе координат Х¢О¢У¢, где О¢(–1, 3). Уравнения прямых в этой системе координат можно записать в виде

у ¢ = ±2 х ¢

и легко построить.

4) х ² + 2 ху + у ² – 4 = 0 Þ (х ² + 2 ху + у ²) – 4 = 0,

(х + у)² – 4 = 0 Þ (х + у –2)(х + у +2) = 0,

х + у –2 = 0 и х + у +2 = 0

– две прямые, их легко построить в системе координат ХОУ. Нетрудно построить систему координат, в которой уравнения этих прямых будут заданы в виде х ¢ ²– а ² = 0, или в виде

у ¢ ²– а ² = 0.