КОНТРОЛЬНЫХ РАБОТ
При выполнении контрольных работ требуется строгое соблюдение указанных ниже правил. Работы, выполненные без соблюдения этих правил, могут быть не зачтены.
1. Контрольная работа выполняется в тетради в клетку чернилами любого цвета, кроме красного. Необходимо оставлять поля для замечаний рецензента.
2. На обложке контрольной работы должны быть написаны фамилия и инициалы студента, шифр, название дисциплины, номер и вариант контрольной работы, адрес студента. В конце работы ставится дата ее выполнения и подпись.
3. В работу включаются все задачи, указанные в задании, строго по положенному варианту.
4. Решения задач располагаются в порядке возрастания их номеров, указанных в задании, сохраняя номера задач.
5. Условия задач приводятся полностью. Решения излагаются подробно и аккуратно, объясняются все действия по ходу решения и делаются необходимые чертежи.
6. После получения проверенной работы исправляются отмеченные рецензентом ошибки и выполняются все рекомендации рецензента.
ВОПРОСЫДЛЯ САМОПРОВЕРКИ К КОНТРОЛЬНОЙ
РАБОТЕ №5
1. Дайте определение дифференциального уравнения. Как определяется порядок дифференциального уравнения?
2. Дайте определение общего и частного решений дифференциального уравнения.
3. Сформулируйте задачу Коши.
4. Дайте классификацию дифференциальных уравнений 1-го порядка и укажите способы их решения.
5. Приведите типы дифференциальных уравнений второго порядка, допускающих понижение порядка, и укажите способы понижения порядка таких уравнений.
6. Дайте определение линейного дифференциального уравнения второго порядка. Сформулируйте теорему об общем решении такого уравнения.
7. Как находится общее решение линейного однородного уравне - ния второго порядка с постоянными коэффициентами?
8. Как находится частное решение неоднородного уравнения с правой частью специального вида?
9. Как находится решение неоднородного уравнения методом вариации произвольной постоянной?
10. Запишите систему линейных дифференциальных уравнений с постоянными коэффициентами. Как находится общее решение таких систем методом исключения?
ВОПРОСЫДЛЯ САМОПРОВЕРКИ К КОНТРОЛЬНОЙ
РАБОТЕ №6
1. Дайте определения функции двух переменных, ее области определения и непрерывности.
2. Дайте определения частных производных функции двух переменных.
3. Запишите формулу полного дифференциала для функции двух переменных.
4. Дайте определения производной по направлению и градиента функции двух переменных.
5. Сформулируйте необходимые и достаточные условия экстремума функции двух переменных.
6. Как вычисляются наибольшее и наименьшее значения функции двух переменных в замкнутой области?
7. Дайте определение двойного интеграла в прямоуголь-ной системе координат.
8. Запишите формулу преобразования двойного интеграла от прямоугольных координат к полярным координатам.
9. Запишите формулу вычисления площади плоской фигуры и объема тела с помощью двойного интеграла.
10. Дайте определение тройного интеграла в прямоугольной системе координат.
11. Запишите формулу вычисления объема тела с помощью тройного интеграла.
12. Запишите формулу преобразования тройного интеграла от прямоугольных координат к цилиндрическим и сферическим координатам.
13. Дайте определение криволинейного интеграла.
14. Запишите формулу вычисления криволинейного интеграла посредством сведения его к определенному.
15. Запишите формулу Грина.
16. Дайте определение поверхностного интеграла.
17. Запишите формулу вычисления поверхностного интеграла путем сведения его к двойному интегралу.
18. Запишите формулы Стокса и Остроградского-Гаусса.
19. Дайте определение ротора, дивергенции, циркуляции.
ЗАДАЧИ ДЛЯ КОНТРОЛЬНЫХ ЗАДАНИЙ
Контрольная работа №5 «Дифференциальные уравнения »
Задача №1
Найти общее решение дифференциального уравнения:
1.  ; 11.
; 11.  ;
;
2.  ; 12.
; 12.  ;
;
3. 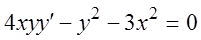 ; 13.
; 13. 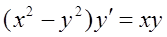 ;
;
4.  ; 14.
; 14.  ;
;
5.  ; 15.
; 15. 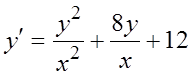 ;
;
6.  ; 16.
; 16.  ;
;
7.  ; 17.
; 17.  ;
;
8. 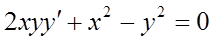 ; 18.
; 18.  ;
;
9.  ; 19.
; 19.  ;
;
10.  ; 20.
; 20.  .
.
Задача №2
Найти частное решение задачи Коши:
1.  ,
,  .
.
2. 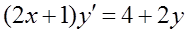 ,
,  .
.
3.  ,
,  .
.
4.  ,
,  .
.
5. 
 .
.
6.  ,
,  .
.
7. 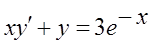 ,
,  .
.
8.  ,
,  .
.
9.  ,
,  .
.
10.  ,
,  .
.
11.  ,
, 
 .
.
12.  ,
,  .
.
13.  ,
,  .
.
14.  ,
,  .
.
15.  ,
,  .
.
16.  ,
,  .
.
17.  ,
,  .
.
18. 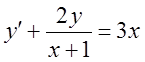 ,
,  .
.
19.  ,
,  .
.
20.  ,
,  .
.
Задача №3
Найти общее решение дифференциального уравнения
1.  . 2.
. 2. 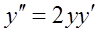 .
.
3.  . 4.
. 4.  .
.
5.  . 6.
. 6.  .
.
7.  . 8.
. 8.  .
.
9. 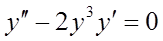 . 10.
. 10.  .
.
11.  . 12.
. 12.  .
.
13.  . 14.
. 14. 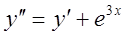 .
.
15.  . 16.
. 16.  .
.
17.  . 18.
. 18.  .
.
19.  . 20.
. 20.  .
.
Задача №4
Записать вид частного решения дифференциального уравнения
1.  .
.
2.  .
.
3.  .
.
4.  .
.
5.  .
.
6.  .
.
7. 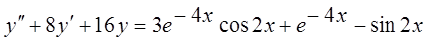 .
.
8.  .
.
9. 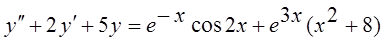 .
.
10.  .
.
11. 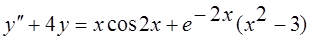 .
.
12.  .
.
13.  .
.
14.  .
.
15. 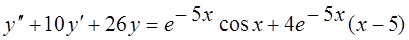 .
.
16  .
.
17. 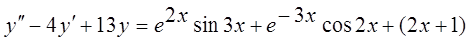 .
.
18.  .
.
19.  .
.
20.  .
.
Задача №5
Найти частное решение линейного неоднородного дифференциального уравнения второго порядка, удовлетворяющее начальным условиям.
1. 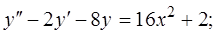
 0;
0;  5.
5.
2 
 1;
1;  2
2
3. 
 2;
2;  5.
5.
4. 
 1;
1;  1.
1.
5. 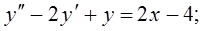
 1;
1;  1.
1.
6. 
 2;
2;  7.
7.
7. 
 0;
0;  1.
1.
8. 
 3;
3;  5.
5.
9. 
 2;
2;  4.
4.
10. 
 0;
0;  3.
3.
11. 
 1;
1;  2.
2.
12. 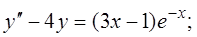
 0;
0;  –4.
–4.
13. 
 –1;
–1;  –4.
–4.
14. 
 2;
2;  4.
4.
15. 
 3;
3;  5.
5.
16. 
 1;
1;  1.
1.
17. 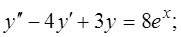
 2;
2;  0.
0.
18. 
 1;
1;  4
4
19. 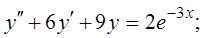
 1;
1;  –3.
–3.
20. 
 1;
1;  2.
2.
Задача №6
Методом исключения неизвестных найти общее решение системы дифференциальных уравнений
1.  2.
2.  3.
3. 
4.  5.
5.  6.
6. 
7. 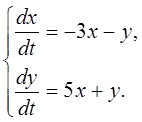 8.
8. 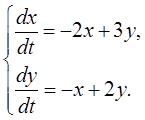 9.
9. 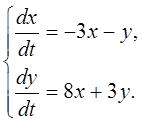
10.  11.
11.  12.
12. 
13.  14.
14.  15.
15.  16.
16.  17.
17.  18.
18. 
19.  20.
20. 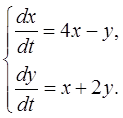
Контрольная работа №6. « Дифференциальное исчисление функции нескольких переменных, кратные и криволинейные интегралы »
Задача №1
Найти все производные второго порядка функции
1.  . 2.
. 2. 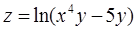 . 3.
. 3.  .
.
4.  . 5.
. 5.  . 6.
. 6.  .
.
7.  . 8.
. 8.  . 9.
. 9.  .
.
10.  . 11.
. 11.  . 12.
. 12.  .
.
13. 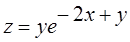 . 14.
. 14.  . 15.
. 15.  .
.
16.  . 17.
. 17.  . 18.
. 18.  .
.
19.  . 20.
. 20. 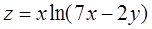 .
.
Задача № 2
Найти наибольшее и наименьшее значения функции  в замкнутой области D, ограниченной заданными линиями:
в замкнутой области D, ограниченной заданными линиями:
1. 

2. 
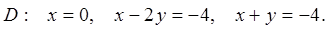
3. 

4. 

5. 

6. 

7.  ;
; 
8. 

9. 

10. 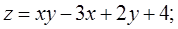

11. 

12. 

13. 

14. 

15. 

16. 

17. 

18. 

19. 

20. 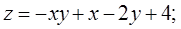

Задача № 3
Даны: функция  , точка
, точка  и вектор
и вектор  . Найти:
. Найти:
1) grad z в точке  ;
;
2) производную в точке  по направлению вектора
по направлению вектора 
1. 
 (1;1);
(1;1);  .
.
2. 
 (2;1);
(2;1); 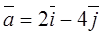 .
.
3. 
 (1;0);
(1;0); 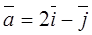 .
.
4. 
 (–1;2);
(–1;2); 
5. 
 (2; –1);
(2; –1); 
6. 
 (2;3);
(2;3);  .
.
7. 
 (0;2);
(0;2); 
8. 
 (–1; –1);
(–1; –1); 
9. 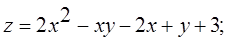
 (0;1);
(0;1);  .
.
10. 
 (1;3);
(1;3); 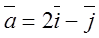 .
.
11. 
 (0;0);
(0;0); 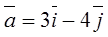 .
.
12. 
 (1;1);
(1;1);  .
.
13. 
 (1;1);
(1;1);  .
.
14. 
 (0;1);
(0;1);  .
.
15. 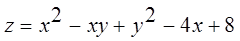 ;
;  (1;3);
(1;3);  .
.
16. 
 (1; –2);
(1; –2);  .
.
17. 
 (5;4);
(5;4);  .
.
18. 
 (0;1);
(0;1);  .
.
19. 
 (–1;1);
(–1;1);  .
.
20. 
 (1; –2);
(1; –2);  .
.
Задача № 4
Вычислить объем тела, ограниченного поверхностями:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 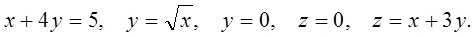
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 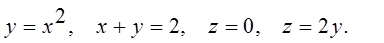
20. 
Задача № 5
Вычислить криволинейный интеграл вдоль заданной кривой L:
1.  ;
; 
2.  ;
; 
3.  ;
; 
4.  ;
; 
5.  ;
; 
6.  ;
; 
7.  ;
; 
8.  ;
; 
9.  ;
; 
10.  ;
; 
11.  ;
; 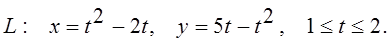
12.  ;
; 
13.  ;
; 
14.  ;
; 
15.  ;
; 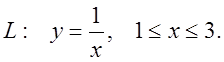
16.  ;
; 
17.  ;
; 
18.  ;
; 
19.  ;
; 
20. 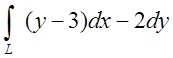 ;
; 
ПРИМЕРЫРЕШЕНИЯ ЗАДАЧ
К КОНТРОЛЬНОЙ РАБОТЕ №5
Для решения задач 1–2 необходимо изучить пункты 1,2 программы.
Пример 1. Найти общее решение дифференциального уравнения  = tg x tg y.
= tg x tg y.
Решение. Полагая  =
=  , получим
, получим  = tg x tg y. Разделяя переменные, приходим к уравнению сtg у dy = tg x dx. Интегрируем:
= tg x tg y. Разделяя переменные, приходим к уравнению сtg у dy = tg x dx. Интегрируем:
 сtg у dy=
сtg у dy=  tg x dx, или ln
tg x dx, или ln  = – ln
= – ln  +ln c.
+ln c.
(Постоянная интегрирования обозначена ln c). Отсюда находим sin y =c/ cos x или sin y cos x =c – общее решение уравнения.
Пример 2. Найти общее решение дифференциального уравнения с разделяющимися переменными.
(1+  ) dy +ydx= 0.
) dy +ydx= 0.
Решение. Преобразуем уравнение к виду  = –
= –  . Интегрируя получим
. Интегрируя получим 
 = –
= –  , или ln
, или ln  =
=
= – arctg x + c. Общее решение можно записать в виде  .
.
Пример 3. Найти общее решение однородного дифференциаль-ного уравнения х  = х + 2 у.
= х + 2 у.
Решение. Однородное дифференциальное уравнение первого порядка можно привести к виду  = f (
= f (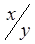 ). Чтобы решить уравнение проводят замену
). Чтобы решить уравнение проводят замену  , где u (x) – новая неизвестная функция, после чего уравнение преобразуется в уравнение с разделяющимися переменными.
, где u (x) – новая неизвестная функция, после чего уравнение преобразуется в уравнение с разделяющимися переменными.
Преобразуя исходное уравнение, получим  =
=  или
или  =
=  – однородное уравнение. Полагаем
– однородное уравнение. Полагаем  , тогда
, тогда  = u + x
= u + x  . Уравнение запишется x
. Уравнение запишется x  + u = 1 + 2 u или
+ u = 1 + 2 u или  х = 1+ u. Решаем полученное уравнение с разделяющимися переменными
х = 1+ u. Решаем полученное уравнение с разделяющимися переменными
 =1 + u или
=1 + u или  =
=  , интегрируем
, интегрируем 
 =
= 
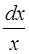 , получим ln
, получим ln  = ln
= ln  + ln
+ ln  . Откуда 1+ u =cx или u= cx – 1. Возвращаясь к старой переменной у по формуле u=
. Откуда 1+ u =cx или u= cx – 1. Возвращаясь к старой переменной у по формуле u= 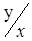 , получим обще решение
, получим обще решение  .
.
Пример 4. Найти частное решение линейного дифференциаль-ного уравнения первого порядка, удовлетворяющее начальному условию:
 −
−  =
=  ,
,  (0) = 1.
(0) = 1.
Решение. Решение уравнения ищем в виде произведения двух функций y = u (x) v (x), вычисляя производную, получим
 =
=  .
.
После подстановки в уравнение, запишем
 =
=  или
или
 =
=  .
.
Выберем функцию v (x) такой, чтобы выполнялось условие  =0. Разделяя переменные в этом уравнении, находим
=0. Разделяя переменные в этом уравнении, находим  или
или  . После интегрирования обеих частей равенства, получим ln
. После интегрирования обеих частей равенства, получим ln  = 2 ln
= 2 ln  + с, т.к. достаточно найти хотя бы одно решение отличное от нуля, то положим с = 0. Тогда
+ с, т.к. достаточно найти хотя бы одно решение отличное от нуля, то положим с = 0. Тогда  =
=  . Подставляя найденное значение v (x) в исходное уравнение и учитывая, что
. Подставляя найденное значение v (x) в исходное уравнение и учитывая, что  =0, запишем
=0, запишем  =
=  или
или  , откуда после интегрирования получим
, откуда после интегрирования получим  . Окончательно общее решение запишется
. Окончательно общее решение запишется
y = u (x) v (x)  .
.
Найдем частное решение, удовлетворяющее начальному условию
 (0) = 1.
(0) = 1.  (0)
(0)  = 1. Откуда
= 1. Откуда  , тогда частное
, тогда частное
решение запишется  .
.
Для решения задачи 3 необходимо изучить пункт 3 программы.
Некоторые типы уравнений второго порядка приводятся к уравнениям первого порядка. К ним относятся:
1) Уравнения вида  , которые не содержат явным образом
, которые не содержат явным образом  . Обозначим производную
. Обозначим производную  через
через  т.е.
т.е.
 Тогда
Тогда 
Подставляя эти выражения производных в исходное уравнение, получим уравнение первого порядка.
2) Уравнения вида  , которые не содержат явным образом
, которые не содержат явным образом  .
.
Положим  и, так как
и, так как 
 то для определения производной
то для определения производной  применим правило дифференцирования сложной функции
применим правило дифференцирования сложной функции

Подставляя выражения производных в исходное уравнение, получим уравнение первого порядка относительно вспомогательной функции 
 .
.
Пример 5. Решить уравнение  .
.
Решение. Вводим новую функцию  ,
,  , тогда
, тогда 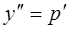 . Подставив ее в уравнение, имеем
. Подставив ее в уравнение, имеем
 .
.
Это линейное уравнение первого порядка относительно  и его решение разыскиваем в виде произведения
и его решение разыскиваем в виде произведения 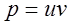

Учитывая требования  ,
,  , находим функцию
, находим функцию  :
:  подставляем в уравнение для определения
подставляем в уравнение для определения 

Отсюда

 .
.
Таким образом,  , и можно найти функцию y
, и можно найти функцию y
 ,
, 
Пример 6. Найти общий интеграл уравнения  .
.
Решение. Уравнение не содержит явным образом  . Следовательно, допускается понижение порядка. Обозначим
. Следовательно, допускается понижение порядка. Обозначим 
 Тогда
Тогда 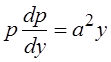 .
.
Получим уравнение с разделяющимися переменными  , интегрируя которое, находим
, интегрируя которое, находим  или
или
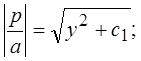


Откуда 
Перед решением задач 4 и 5 следует изучить пункты 4, 5 програм-мы.
Пусть имеем уравнение
 , (1)
, (1)
где p и q - действительные числа.
Для уравнения с постоянными коэффициентами в некоторых случаях частное решение можно найти, не прибегая к интегрированию.
1. Пусть правая часть уравнения (1) представляет собой произведение показательной функции на многочлен, т.е. имеет вид  , где
, где