Плоскость в пространстве

Предмет аналитической геометрии

Аналитическая геометрия – это раздел геометрии, в котором для исследования геометрических объектов (точек, прямых, плоскостей, линий, поверхностей, тел) используются средства алгебры и математического анализа.

В основе аналитической геометрии лежит метод координат. Суть его в следующем: на плоскости или в пространстве фиксируется вспомогательный геометрический объект – система координат, которая позволяет каждой точке плоскости или пространства ставить в соответствие систему чисел, называемых координатами точки, а всякий геометрический объект рассматривается, как совокупность точек, обладающий общим (характистическим) свойством. Это свойство с помощью координат точек можно описать в виде уравнения, неравенства, системы уравнений или неравенств (а, значит, с помощью функций). Тогда изучение объекта можно свести к изучению этих уравнений, неравенств (функций).

Основными задачами аналитической геометрии являются следующие:

1) Используя характеристическое свойство точек объекта, описать его с помощью уравнения, неравенства.

2) Зная алгебраический образ геометрического объекта (его уравнение, неравенство, …) изучить свойства этого объекта.

В дальнейшем мы будем предполагать, что на плоскости или в пространстве задана ДПСК. Тогда каждой точке плоскости (пространства) соответствует пара чисел (х, у) (тройка чисел (х, у, z)) и наоборот, каждой совокупности чисел соответствует точка. Так как пара (х, у) есть числовая строка длины два, а тройка (х, у, z) есть числовая строка длины три, то множество точек плоскости и пространства можно идентифицировать с координатными пространствами R² и R³соответственно. Поэтому в дальнейшем множество точек плоскости будем обозначать R², а множество точек пространства – R³.

Определение 1.

Уравнением линии на плоскости (в R²) называется такое уравнение с двумя переменными, которому удовлетворяют координаты всех точек заданной линии и только они.

В общем виде уравнение линии на плоскости записывают так

F(x, y) = 0.

Если F₁(x, y) = 0 –уравнение одной линии, а F₂(x, y) = 0 –уравнение другой, то точки пересечения этих линий находят из системы

Уравнение линии может быть задано в виде у = f (x) или (параметрическое задание линии).

С точки зрения математического анализа, уравнение линии – это задание функции (явное или неявное), графиком которой данная линия является, причем однозначность функции в этом случае не оговаривается.

Чтобы составить уравнение линии, нужно

1) взять произвольную точку М(х, у) этой линии (ее называют текущей точкой);

2) записать характеризующее свойство точек линии в виде символьного равенства;

3) входящие в это равенство отрезки выразить через координаты точки М(х, у) и других известных из условия задачи точек;

4) упростить полученное уравнение.

Пример: Составить уравнение и построить линию, каждая точка которой равноудалена от точки А(2, 0) и от прямой у – 2 = 0.

Решение:

Сделаем схематичный чертеж (рис.1). Пусть точка М(х, у) – текущая точка искомой кривой. Тогда, по условию,

|AM| = |PM|,

где РМ – перпендикуляр, опущенный из точки М на прямую у – 2 = 0.

Запишем это равенство через координаты точек А, М, Р. Имеем

|AM| = .

Из чертежа легко определяем координаты точки Р (х, 2), тогда

|PM| = .

Получим – это и есть искомое уравнение линии. Преобразуем его.

х ² – 4 х + 4 + у ² = у ² – 4 у + 4,

х ² – 4 х = –4 у,

у = 1 – 0,25(х –2)² – уравнение параболы (рис.2).

Определение 2.

Уравнением поверхности в пространстве (в R³) называется такое уравнение с тремя переменными, которому удовлетворяют координаты всех точек поверхности и только они.

Уравнение поверхности записывают в виде F(x, y, z) = 0.

Линию в пространстве R³ можно рассматривать как пересечение двух поверхностей, поэтому в R³ линия определяется системой уравнений этих поверхностей:

Линию в пространстве можно также задать параметрическими уравнениями

каждое уравнение этой системы определяет закон изменения соответствующей координаты текущей точки линии в зависимости от изменения некоторого параметра t. Такими уравнениями может быть задана траектория движения материальной точки.

Прямая на плоскости

Пусть в ДПСК дана прямая l, М₀ – некоторая фиксированная точка этой прямой, а М – текущая точка прямой l. Обозначим ` S произвольный вектор, параллельный этой прямой (рис.3), а ` r = и` r ₀ = – радиус векторы точек М и М₀ в ПДСК. Тогда можно записать = ` r – ` r ₀.

Очевидно, точка М лежит на прямой l тогда и только тогда, когда вектор параллелен этой прямой, и, следовательно, параллелен вектору `S. Значит, должно выполняться условие = , где t ÎR – некоторое число, для каждой точки М – свое. Следовательно, для точек прямой l справедливо равенство` r – ` r ₀ = , или

`r =` r ₀ + (1).

Это равенство называется векторным уравнением прямой. Вектор `S называется направляющим вектором этой прямой.

Таким образом, всякая прямая может быть однозначно задана точкой (М₀) и вектором (параллельным этой прямой).

Мы рассмотрели случай пространственной прямой, но нигде это явно не отражалось. Значит, векторное уравнение (1) определяет как пространственную, так и плоскую прямую.

Рассмотрим ПДСК в R². Пусть М₀(х ₀, у ₀), М(х, у), `S = (m, n). Из равенства (1) получим (х, у) = (х ₀, у ₀) + t (m, n), или

, (2)

Эти уравнения называются параметрическими уравнениями прямой на плоскости. Если уравнения (2) преобразовать к виду

то отсюда следует уравнение

, (3)

которое называется каноническим уравнением прямой.

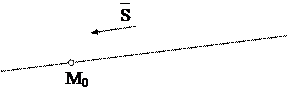Напомним еще раз, что и в уравнении (3), и в уравнении (2) (х ₀; у ₀) – координаты точки, лежащей на прямой, (т; п) – координаты направляющего вектора `S этой прямой (вектора, параллельного прямой):

Эти уравнения называют также уравнениями прямой, проходящей через заданную точку параллельно заданному вектору.

Если вектор `S = , где М₀(х ₀, у ₀) и М₁(х ₁, у ₁) – точки, лежащие на прямой l, то `S = (х ₁ – х ₀, у ₁ – у ₀), следовательно, уравнение (3) можно представить в виде

, (4)

– уравнения прямой, проходящей через две точки М₀(х ₀; у ₀) и М₁(х ₁; у ₁).
Продолжим преобразование уравнения (3):

п (х – х ₀) = т (у ₁ – у ₀), п (х – х ₀) – т (у ₁ – у ₀) = 0.

Обозначим здесь А = п, В = – т, получим

А(х – х ₀) + В(у ₁ – у ₀) = 0, (5).

Обозначим`N = (А, В). Нетрудно убедиться в том, что векторы `N и `S ортогональны:

(`N,`S) = А т + В п = пт + (– т) п = 0.

Поэтому уравнение (5) есть уравнение прямой, проходящей через точку М(х ₀; у ₀) перпендикулярно вектору `N = (A; B). Вектор `N, перпендикулярный заданной прямой, называется нормальным вектором этой прямой.
Если в уравнении (5) А и В – произвольные числа, то это уравнение называют уравнением пучка прямых, проходящих через точку М₀(х ₀, у ₀).

В уравнении (5) раскроем скобки

А х + В у +(–А х ₀ – В у ₀) = 0

и обозначим С = –А х ₀ – В у ₀. Получим уравнение

А х + В у + С = 0, (6)

– общее уравнение прямой. Коэффициенты А и В в общем уравнении определяют координаты нормального вектора этой прямой:`N = (A; B) ^ l.

Справедлива теорема:

Теорема.

Любое уравнение первой степени (линейное) относительно переменных х и у определяет на плоскости прямую линию, и наоборот, любая прямая на плоскости может быть задана линейным уравнением вида

А х + В у + С = 0.

Исследуем расположение прямой относительно системы координат по ее общему уравнению А х + В у + С = 0.

Если С = 0, А, В ¹ 0, то прямая Ах + Ву = 0проходит через начало координат (координаты точки (0, 0) удовлетворяют этому уравнению, значит, она лежит на данной прямой).

Если А = 0, а В, С ¹ 0, то прямая Ву + С = 0 параллельна оси ОХ (нормальный вектор этой прямой имеет координаты (0, В), т.е. перпендикулярен оси ОХ, поэтому прямая и ось параллельны).

Если В = 0, А, С ¹ 0, то прямая Ах + С = 0 параллельна оси ОУ (в этом случае нормальный вектор имеет координаты (А, 0), т.е. параллелен оси ОХ, и, значит, перпендикулярен оси ОУ, поэтому и прямая параллельна оси ОУ)

Если А = 0, С = 0, В ¹ 0, то уравнение Ву = 0 определяет ось ОХ (прямая параллельна оси ОХ и проходит через начало координат).

Если В = 0, С = 0, А ¹ 0, то уравнение Ах = 0 определяет ось ОУ.

Если В ¹ 0, то Ву = Ах – C, или . Обозначим k = – , а b = – 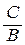, тогда уравнение (6) примет вид

y = kx + b, (7)

– уравнение с угловым коэффициентом. Коэффициенты k и b имеют простой геометрический смысл:

k = tga, где a – угол между прямой и положительным направлением оси ОХ (k называют угловым коэффициентом прямой),

b – ордината точки пересечения прямой с осью ОУ (величина отрезка, отсекаемого прямой на этой оси). Если k = 0, то прямая параллельна оси ОХ; если b = 0, то прямая проходит через начало координат.

Если С ¹ 0, то Ах + Ву = – С, откуда

, или .

Обозначим здесь а = – , b = – 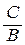, получим

, (8)

– уравнение прямой в отрезках на осях.

Уравнение получило такое название, исходя из геометрического смысла чисел а и b:

а – величина отрезка, отсекаемого прямой на оси ОХ,

b – величина отрезка, отсекаемого прямой на оси ОУ.

Таким образом, прямая (8) проходит через точки (0; b) и (а; 0).

Из всего вышесказанного можно сделать следующий вывод:

чтобы найти уравнение прямой, достаточно знать:

· либо две точки этой прямой (уравнение(4))

· либо точку и вектор – параллельный этой прямой (направляющий, уравнения (1), (2) (3)) или перпендикулярный этой прямой (нормальный, уравнение (5) или (6)).

· точку и угол наклона прямой к одной из осей координат.

Исследовать взаимное расположение прямых на плоскости можно с помощью соответствующих им векторов и точек, принадлежащих этим прямым. Если `N₁, `S₁– нормальный и направляющий векторы прямой l ₁ соответственно, а `N₂, `S₂– нормальный и направляющий векторы прямой l ₂, то

· l ₁|| l ₂ Û` N₁||`N₂, или`S₁||`S₂,
или `N₁^`S₂(рис. а);

· l ₁^ l ₂Û `N₁^`N₂, или `S₁^`S₂,
или `N₁||`S₂ (рис. б);

б)

· l ₁= l ₂Û l ₁|| l ₂и существует точка М:

МÎ l ₁, МÎ l ₂;

· угол между прямыми можно найти как угол между соответствующими им векторами: (либо как смежный к этим углам), (рис.в);

· координаты точки М пересечения двух прямых есть решение системы уравнений этих прямых.

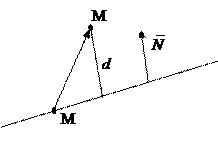Расстояние d от точки М(х ₀; у ₀) до прямой Ах + Ву + С = 0 находят по формуле

Действительно, пусть М₁(х ₁, у ₁) произвольная точка этой прямой, а `N =(А, В) – ее нормальный вектор. Тогда искомое расстояние

d = = .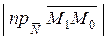

Поскольку = (х ₀ – х ₁, у ₀ – у ₁), то

d = =

Т.к. точка М₁Î l, то Ах ₁ + Ву ₁+ С = 0, откуда – Ах ₁ – Ву ₁= С. Тогда получаем d = .

Замечание: Если М₀(0,0), то d = | С |, т.е. коэффициент С в общем уравнении прямой характеризует отклонение прямой от начала координат.

Лекции 11,12. Плоскость и прямая в пространстве

Содержание лекции: Плоскость в пространстве, различные виды уравнений плоскости, взаимное расположение. Прямая в пространстве, виды уравнений прямой. Взаимное расположение прямых, прямой и плоскости.

Плоскость в пространстве

Рис.4

Рассмотрим ДПСК {O,` i,` j,` k } в пространстве R³. Пусть a – некоторая плоскость и вектор

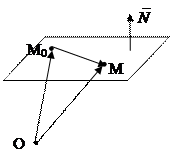
перпендикулярен a. Зафиксируем на плоскости a произвольную точку М₀ и возьмем текущую точку М пространства (рис.4). Обозначим ` r =

и` r ₀ =

. Тогда

= ` r – ` r ₀, а точка МÎa тогда и только тогда, когда векторы `N и

ортогональны. Последнее возможно, когда

` N. = 0, т.е. ` N. (` r – ` r ₀) = 0 (9)

–это уравнение называется векторным уравнением плоскости. Вектор `N называют нормальным вектором плоскости.

Если `N =(А, В, С), М₀(х ₀, у ₀, z ₀), М(х, у, z), то уравнение (9) примет вид

А(х – х ₀) + В(у – у ₀) + С(z – z ₀) = 0, (10).

Это уравнение называют уравнением плоскости, проходящей через заданную точку перпендикулярно заданному вектору.

Как известно, через три точки можно провести единственную плоскость. Пусть М₁(х ₁, у ₁, z ₁), М₃(х ₂, у ₂, z ₂), М₃(х ₃, у ₃, z ₃)Îa. Найдем уравнение этой плоскости. Согласно векторному уравнению (9), чтобы записать это уравнение, необходимо знать точку плоскости и нормальный вектор. Точка у нас есть (например М₁). А в качестве нормального вектора подойдет любой вектор, перпендикулярный этой плоскости. Известно, что векторное произведение двух векторов перпендикулярно плоскости, в которой лежат эти векторы. Следовательно, векторное произведение векторов и можно взять в качестве нормального вектора плоскости a:

`N = ´

Тогда уравнение плоскости a в векторной форме имеет вид

. ( ´ ) = . . = 0.

(заметим, что получили условие компланарности векторов , , ).

Через координаты точек М₁, М₂, М₃ и М это уравнение запишется так

, (11)

и называется уравнением плоскости, проходящей через три заданные точки М₁(х ₁, у ₁, z ₁), М₂(х ₂, у ₂, z ₂), М₃(х ₃, у ₃, z ₃).

Рассмотрим вновь уравнение (9), преобразуем его:

Ах + Ву + Cz +(– Ах ₀ – Ву ₀ – Cz ₀) = 0,

Ах + Ву + Cz +D = 0, где D = (– Ах ₀ – Ву ₀ – Cz ₀).

Уравнение

Ах + Ву + Cz +D = 0, (12)

называется общим уравнением плоскости. Здесь вектор`N = (A, B, C) – нормальный вектор плоскости (т.е. вектор, перпендикулярный плоскости).

Справедлива теорема:

Теорема.

В пространстве R³ всякая плоскость может быть описана линейным относительно переменных x y, z уравнением и наоборот, любое уравнение первой степени определяет некоторую плоскость.

Изучим расположение плоскости относительно системы координат по ее общему уравнению Ах + Ву + Cz +D = 0.

Если коэффициент D = 0, то координаты точки О(0, 0, 0) удовлетворяют уравнению Ах + Ву + Cz = 0, значит, эта точка лежит на плоскости, т.е. плоскость с уравнением Ах + Ву + Cz = 0 проходит через начало координат.

Если в общем уравнении плоскости отсутствует одна из переменных (соответствующий коэффициент равен нулю), то плоскость параллельна одноименной оси координат. Например, уравнение Ах + Cz + D = 0 определяет плоскость, параллельную оси ОУ. Действительно, вектор нормали имеет координаты `N = (А, 0, С) и легко проверить, что `N ^` j. Но если плоскость и вектор перпендикулярны одному и тому же вектору, то они параллельны. Плоскость с уравнением Ву + Cz = 0, в таком случае, проходит через ось ОХ (т.е. эта ось лежит на плоскости)

Отсутствие двух переменных в уравнении плоскости означает, что плоскость параллельна соответствующей координатной плоскости, например, уравнение вида Ах + D = 0 определяет плоскость, параллельную плоскости УОZ. Вектор нормали имеет координаты `N = (А, 0, 0), он коллинеарен вектору ` i, и,следовательно, плоскость перпендикулярна вектору ` i, или параллельна плоскости УОZ.

Уравнения координатных плоскостей имеют вид:

пл. ХОУ: z = 0, пл. XOZ: y = 0, пл. YOZ: x = 0.

Действительно, плоскость ХОУ проходит через начало координат (D = 0) и вектор ` k =(0, 0, 1) – ее нормальный вектор. Аналогично плоскости ХОZ и УОZ проходят через начало координат(D = 0) и векторы ` j =(0, 1, 0) и ` i = (1,0,0) – их нормали соответственно.

Если D¹0, то преобразуем общее уравнение так

Ах + Ву +С z = – D, , .

Обозначив здесь , , , получим уравнение
, (13)

которое называется уравнением плоскости в отрезках на осях. Здесь а, b, c –величины отрезков, отсекаемых плоскостью на осях координат (рис.5). Это уравнение удобно использовать для построения плоскости в системе координат. Нетрудно убедиться, что точки (а, 0, 0), (0. b, 0), (0, 0, с) лежат на плоскости. Прямые, проходящие через эти точки, называются следами плоскости на координатных плоскостях.

Например, построим плоскость

2 х – 3 у + 4 z –12 = 0.

Приведем это уравнение к виду (13), получим

Для построения плоскости в системе координат, отметим на оси ОХ точку (6, 0, 0), на оси ОУ точку (0, -4, 0), на оси ОZ – (0, 0, 3), соединим их отрезками прямы (следы плоскости). Полученный треугольник есть часть искомой плоскости, заключенная между осями координат.

-4

Таким образом, чтобы найти уравнение плоскости, достаточно знать

- либо нормальный вектор этой плоскости и любую ее точку (уравнение (10));

- либо три точки, лежащие на плоскости (уравнение (11)).

Взаимное расположение плоскостей в пространстве удобно изучать с помощью соответствующих им векторов. Если a – плоскость с нормальным вектором `N, то

· a₁ || a₂ Û `N₁ ||`N₂((рис.А);

· a₁ ^ a₂ Û `N₁ ^`N₂ (рис.Б);

Рис.А

Рис.Б

· Угол 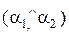между двумя плоскостями равен углу между их нормальными векторами или является смежным к нему, причем .

· Расстояние от точки М₀(х ₀, у ₀, z ₀) до плоскости Ах + Ву + Сz +D = 0 находят по формуле

Вывод формулы аналогичен тому, как это было проделано для прямой на плоскости. Провести его самостоятельно.

Прямая в пространстве.

Рассмотрим векторное уравнение прямой ` r =` r ₀ + (1), где ` r ₀ – радиус-вектор произвольной фиксированной точки прямой, а ` S – направляющий вектор этой прямой (т.е. вектор, параллельный этой прямой). Если М₀(х ₀, у ₀, z ₀) и ` r ₀ = (m, n. p), то из (1) имеем

(х, у, z) = (х ₀, у ₀, z ₀) + t (m, n. p),

откуда получим

, (14)

– параметрические уравнения прямой в пространстве. Исключая t из этих уравнений получим

, (15)

– канонические уравнения прямой.

Если известны две точки М₁(х ₁, у ₁, z ₁) и М₂(х ₂, у ₂, z ₂) прямой, то ее уравнения можно записать в виде

, (16)

– уравнения прямой, проходящей через две заданные точки М₁(х ₁, у ₁, z ₁), М₂(х ₂, у ₂, z ₂).

Прямую в пространстве можно рассматривать как линию пересечения двух плоскостей, поэтому она может быть задана системой двух линейных уравнений – уравнений плоскостей, пересечением которых является:

. (17)

При этом говорят, что заданы общие уравнения прямой в пространстве.

Здесь a₁: А ₁ х + В ₁ у + C ₁ z + D ₁ = 0 и a₂: А ₂ х + В ₂ у + C ₂ z + D ₂ = 0 – плоскости, линией пересечения которых является данная прямая l. Заметим, что направляющий вектор `S прямой l ортогонален векторам `N₁и`N₂ – нормальным векторам плоскостей

Таким образом, чтобы найти уравнения прямой в пространстве, достаточно знать

· либо две ее точки (уравнения (16));

· либо точку и направляющий (параллельный) вектор этой прямой (уравнения 14 или 15);

· либо две плоскости, пересечением которых прямая является (уравнения 17).

Заметим, что из канонических уравнений прямой легко определить пару плоскостей, пересечением которых является данная прямая. Достаточно рассмотреть «парные» равенства, например,

, откуда получим

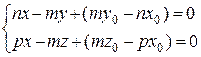
Т.е. прямая представлена как пересечение плоскостей, параллельных осям координат (первая параллельна оси ОZ, вторая – оси ОУ).

Таким образом, от канонических уравнений (или уравнений вида (16)) нетрудно перейти к общим уравнениям прямой в R³.

Наоборот, если по общим уравнениям (17) нужно записать канонические уравнения, то это можно сделать двумя способами:

1) Найти общее решение СЛУ (17) (она всегда совместна и неопределенна, т.к. существует линия пересечения данных плоскостей); по общему найти два произвольных частных решения – две точки искомой прямой; по ним записать уравнение (16) и преобразовать в(15).

2) Найти частное решение СЛУ (17), придав какое-либо значение одной из переменных. Это можно сделать, т.к. система содержит 3 неизвестных и два уравнения, ранг системы равен 2, т.к. плоскости пересекаются, а не совпадают, значит, одна переменная – свободная, ей придаем произвольное значение. Затем найти направляющий вектор`S = `N₁´`N₂, где `N₁и`N₂ – нормальные векторы плоскостей, уравнения которых указаны в системе (17). Указанный вектор является направляющим для данной прямой, т.к., по определению от перпендикулярен векторам `N₁и`N₂. Записать уравнение (15).

Например, найдем канонические уравнения прямой по ее общим уравнениям

Положив в этих уравнениях z = 0, получим 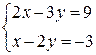, откуда у =15, х =27. Таким образом, точка (27, 15, 0) лежит на данной прямой.

Найдем `S = `N₁´`N₂ = .

Таким образом, `S = (-9, -5, -1). Тогда канонические уравнения прямой имеют вид

Изучение взаимного расположения прямых и плоскостей в пространстве может быть сведено к изучению взаимного расположения соответствующих этим прямым и плоскостям векторов и точек.

l ₁ || l ₂Û `S₁ || `S₂;

· a || l Û `N ^`S

· a ^ l Û `N ||`S

· l Î a Û `N ^`S и $ М₀Îa, М₀Î l.

· Угол между прямой и плоскостью равен углу, дополнительному к углу между нормальным вектором `N плоскости a и направляющим вектором `S прямой l, т.е. = –

Плоскость в пространстве

Поиск по сайту