Несобственные интегралы
Ранее мы познакомились с определенным интегралом (интегралом Римана) и его приложениями. Было установлено, что интеграл Римана существует при выполнении двух условий: подынтегральная функция должна быть ограниченной, непрерывной или кусочно-непрерывной на прямолинейном отрезке интегрирования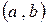 
, причем 
и 
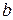должны принимать конечные значения
На практике встречаются случаи, когда необходимо снять хотя бы одно из этих ограничений. Очевидно, приходится вводить другие интегралы, которые в отличие от определенных интегралов, называемых иногда собственными, называют несобственными интегралами.
Несобственные интегралы бывают двух типов (классов). Интегралы с бесконечными пределами и интегралы от неограниченных функций. Ясно, что каждый из этих интегралов снимается одно из ограничений.
Интегралы с бесконечными пределами
Таких интегралов три, и вводятся они следующим образом.
I.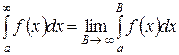 
. Этот интеграл называется интегралом с бесконечным верхним пределом. Если предел существует и имеет конечное значение, интеграл называют сходящимся, он равен значению предела. Если предел не существует или равен 
, он – расходящийся.
II.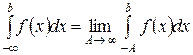 
. Этот интеграл с бесконечным нижним пределом является сходящимся, если предел существует и конечен, и расходящимся в противном случае.
III. 
. Интеграл с бесконечными пределами сходится, если сходится каждый из интегралов, стоящих в правой части. Если хотя бы один из них расходящийся, расходится интеграл 
.
Рассмотрим интеграл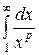 
при различных показателях степени 
.
Если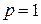 
, то 
. Интеграл расходящийся.
Пусть 
, тогда
.
Если 
, то при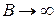 
дробь 
стремится к нулю и интеграл равен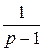 
. Если 
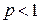, то выражение 
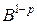стремится к 
, и интеграл - расходящийся. Итак,
Примеры вычисления несобственных интегралов
1) 
.
2) 
.
3) 
.
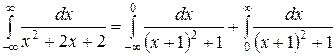Вычислим каждый из интегралов
,
.
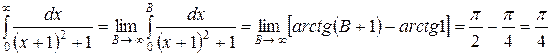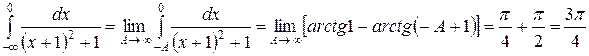Очевидно, 
.
Вычисление интегралов с помощью МАКСИМЫ
Вычислим интеграл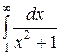 
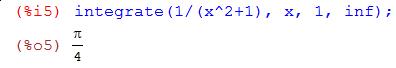
Ответ совпадает с вычисленным выше вручную.
Вычислим интеграл
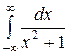
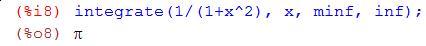
Рассмотрим интеграл
Ответ показывает, что интеграл расходящийся.
Интегралы от неограниченных функций
Несобственные интегралы от неограниченных функций являются другим обобщением определенного интеграла. В этом случае отрезок интегрирования остается конечным, а подынтегральная функция может на интервале интегрирования иметь особую точку, то есть при подходе к этой точке принимать сколь угодно большие значения.
Интегралов от неограниченных функций также три.
I.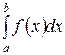 
, причем 
, то есть подынтегральная функция имеет особенность на верхнем пределе. Этот интеграл вводится следующим образом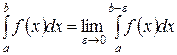 
. В интеграле под знаком предела "вырезана" особая точка, другими словами, отрезок интегрирования сужен так, чтобы особая точка не входила в него. Интеграл в этом случае становится определенным, и вычисление несобственного интеграла сводится к вычислению определенного интеграла, а затем предела от полученного результата. Если предел конечен, то интеграл называется сходящимся, его значение равно вычисленному пределу. Если предел не существует или бесконечен, интеграл расходящийся.
II. 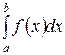, причем 
. Этот интеграл с особенностью на нижнем пределе. Тогда 
. Интеграл сходится и равен значению предела, если этот предел конечен, и расходится, если предел не существует или равен .
III. 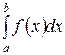, причем 
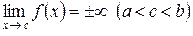, то есть особая точка находится внутри отрезка интегрирования. Тогда 
, и интеграл считается сходящимся, если каждый из интегралов в правой части равенства сходится. В противном случае он – расходящийся.
Пример 1.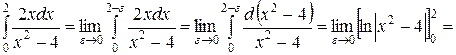 
.
Интеграл расходящийся.
Пример 2.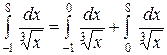 
.
Вычислим интегралы
,
,
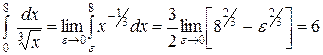оба они сходятся, тогда 
.
Замечание. Здесь не рассматривается понятие главных значений несобственных интегралов. При необходимости с эти материалом можно познакомиться в рекомендованной дополнительной литературе.
Вычисление интегралов с помощью МАКСИМЫ
Подсчитаем интеграл 
с особенностью на нижнем пределе
Он сходящийся.
Вычислим интеграл с особенностью на верхнем пределе
Интеграл расходящийся.