В начале обучения весам сети присваиваются некоторые случайные малые (чтобы предотвратить выход многих нейронов сети в области «насыщения» при использовании сигмоидной функции активации) значения из диапазона [-0.3,0.3]. При обучении сети на ее входы и выходы поступают обучающие сигналы из обучающей последовательности. Выходной сигнал сети сравнивается с обучающим выходным сигналом и определяется сигнал ошибки. Целью обучения является минимизация ошибки распознавания образов, соответствующих тем классам, из образцов которых была построена обучающая последовательность. Обучающие образцы подаются на вход сети в случайном порядке, чтобы сеть не запоминала порядок поступления обучающих сигналов, а формировала признаки распознаваемых классов. Существует два способа обучения персептрона:
Коррекция всех весов производится после предъявления сети каждого обучающего примера.
Коррекция всех весов производится после предъявления сети всей обучающей последовательности или заранее определенной ее части – пакетное (batch) обучение. Просуммированные по всем предъявленным образцам ошибки используются для одновременной коррекции всех весовых коэффициентов.
Процедура минимизации ошибки при этом может быть описана в известных терминах нахождения экстремума функции в предположении, что функционал ошибки на выходе сети имеет минимум.
Одним из часто используемых методов нахождения экстремума является метод градиента. Чтобы применить его к конкретной задаче, необходимо потребовать, чтобы рассматриваемая функция была дифференцируема на всем пространстве поиска, т.е. во всей области допустимых значений аргументов, по которым производится дифференцирование. Для нахождения производной от функционала на выходе сети можно использовать цепное правило дифференцирования. Далее необходимо приравнять полученные производные по всем аргументам к нулю и решить систему нелинейных уравнений для нахождения оптимальных значений. В случае многослойных сетей такой подход сопряжен с большим объемом вычислений и требует затраты больших объемов памяти и машинного времени. Поэтому для настройки сети применяют приближенный метод вычисления минимума, называемый методом наискорейшего спуска. В этом методе поиск решения состоит из ряда итераций, в каждой из которых оптимизируемый параметр изменяет свое значение в соответствии с правилом
вычисленное значение ошибки на выходе сети в момент времени t, h-коэффициент скорости обучения, принимающий значения 0<h<1. Как видим, метод наискорейшего спуска дает правило обучения, имеющее ту же структуру, что и d-правило.
Основная идея обратного распространения состоит в том, как получить оценку ошибки для нейронов скрытых слоев. Заметим, что известные ошибки, делаемые нейронами выходного слоя, возникают вследствие неизвестных пока ошибок нейронов скрытых слоев. Чем больше вес синаптической связи между нейроном скрытого слоя и выходным нейроном, тем сильнее ошибка первого влияет на ошибку второго. Следовательно, оценку вклада каждого весового коэффициента скрытых слоев можно получить, как функцию от взвешенной суммы ошибок последующих слоев. При обучении информация распространяется от низших слоев иерархии к высшим, а оценки ошибок на выходах нейронов скрытых слоев определяются как функции от суммы ошибок последующих слоев. Т.е рассматривается распространение ошибки в обратном направлении по сравнению с направлением распространения сигнала. Поэтому метод получил название «Метода обратного распространения ошибки» (EBP – Error Back Propagation).
В качестве ошибки обучения можно применять любую существенно положительную функцию разности обучающего сигнала и выхода нейрона. Она называется целевой функцией. Согласно методу наименьших квадратов минимизируемой целевой функцией ошибки на выходе сети является величина
где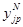 
- реальный выходной сигнал нейрона j выходного слоя N нейронной сети при подаче на ее входы р-го образца, 
- идеальное (желаемое) выходное состояние этого нейрона. В этом случае суммируются ошибки, вычисленные для всех нейронов выходного слоя при предъявлении всех обучающих образов. Такой вид функции ошибки соответствует пакетному (batch) правилу обучения, при котором коррекция весов производится по значению ошибки, накопленной в сети после предъявления всех или заданного числа обучающих примеров. Функция ошибки является в этом случае квадратичной, а поверхность ошибки в пространстве весовых коэффициентов (в области поиска) при использовании сигмоидальной активационной функции имеет сложный рельеф, характеризующийся множеством локальных минимумов.
Целью решения задачи оптимизации является отыскании экстремума функции ошибки. Для этого можно использовать метод градиента, который сводится к вычислению производных от функции ошибки по всем свободным параметрам сети с последующим приравниванием к 0 полученных выражений и решения системы уравнений относительно множества свободных параметров. Для вычисления градиента используется цепное правило дифференцирования. Реальные сети имеют большое число параметров, и такого рода задача становится NP неразрешимой.
Для получения приемлемого решения за разумное время используется метод градиентного спуска, при котором вычисление производных выходного сигнала для каждого нейрона каждого слоя происходит одновременно с вычислением значения выходного сигнала этого слоя. Это возможно благодаря выбору активационной функции, всюду дифференцируемой во всем пространстве свободных параметров сети. Настройка всех весов сети производится одновременно после завершения обратного прохода сигнала ошибки через всю сеть к ее входу.
Производная сигмоидальной функции 
по аргументу net легко вычисляется и равна 
, и может быть реализована аппаратными средствами одновременно с вычислением f(net).
Производная от функции ошибки по весовому коэффициенту 
произвольного слоя определяется как
Здесь 
-выход j-го нейрона n-го слоя. Последний сомножитель в этом выражении равен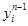 
, второй сомножитель – это производная от активационной функции. Первый сомножитель вычисляется по измеренному значению ошибки в выходном слое с использованием цепного правила дифференцирования для скрытых слоев.
Режимы обучения
Полный цикл обучения с использованием алгоритма ЕВР состоит в представлении на входы сети всех обучающих примеров из обучающей последовательности. Это называют эпохой. Процесс обучения содержит столько эпох, сколько понадобится для стабилизации синаптических весов смещений, и схождения СКО на всем обучающем множестве к заданному значению. В разных эпохах целесообразно использовать меняющийся случайным образом порядок представления обучающих примеров. Это позволяет сделать поиск в пространстве весов стохастическим. Существует два способа организации алгоритма ЕВР.
- Последовательный режим
Последовательный режим (sequential mode) обучения иногда называют стохастическим или итерационным (on–line). В этом режиме корректировка весов производится после подачи на вход каждого примера. Именно этот режим описывается приведенным выше алгоритмом.
- Пакетный режим
В пакетном режиме (batch mode) корректировка весов производится после предъявления сети всех обучающих примеров. Для конкретной эпохи функция стоимости определяется как СКО, представленная в форме
,
где N –мощность обучающей выборки. Значении коррекции веса определяется как
.
Таким образом, в пакетном режиме корректировка весов производится только один раз за эпоху.
Последовательный режим требует меньшего объема памяти для каждого синаптического веса и при случайном порядке предъявления образов в каждой эпохе сокращает до минимума возможность остановки алгоритма в точке локального минимума.
Использование пакетного режима обеспечивает точную оценку вектора градиента. Таким образом, сходимость алгоритма к локальному минимуму гарантируется при довольно простых условиях. Помимо этого, в пакетном режиме легче распараллелить вычисления.
Если данные для обучения являются избыточными (redundant), т.е. содержат несколько копий одних и тех же примеров, предпочтительнее использовать последовательный режим.
В заключение можно сказать, что несмотря на недостатки последовательного режима, он остается очень популярным (особенно при решении задач распознавания образов) по двум практическим причинам:
· Алгоритм прост в реализации.
· Обеспечивает эффективное решение больших и сложных задач.