Ответы и решения
Класс
Каждое задание оценивается в 10 баллов, максимальное количество баллов – 50
1. (1003∙2005 – 1002): (1003 + 2005∙1002) = ((1002 + 1)∙2005 – 1002): (1003 + 2005∙1002)= =(1002∙2005 + 2005 – 1002): (1003 + 2005∙1002) = (1002∙2005 + 1003): (1003 + +2005∙1002) = 1.
2. Для нумерации страниц с первой по девятую понадобится 9 цифр, для нумерации с 10 по 99 понадобится 90∙2 = 180 цифр. Итак, использовано 189 цифр. Осталось 204 - 189 = 15 цифр. Так как с сотой страницы на нумерацию одной страницы требуется три цифры, то всего страниц в книге будет 99 + 15:3 = 104.
3. 8 + 6 = 14 (лет) – суммарный возраст детей. 32-14 = 18 (лет) – разница между возрастом отца и суммарным возрастом детей в данный момент. За каждый год к возрасту отца добавляется 1 год, а к суммарному возрасту детей 2 года. Значит, за каждый прожитый год дети «догоняют» отца на 2 – 1 = 1 год. Следовательно, разница возрастов (18 лет) ликвидируется за 18 лет.
4. а) 3; б) 21
5
 |
 |  |
Ответы и решения
Класс
Каждое задание оценивается в 10 баллов, максимальное количество баллов – 50
1. х = 6
2. Если уменьшить скорость вдвое, то за то же самое время как раз будет пройдена половина пути. (v /2· t = s /2.) Тем самым, автобус проехал половину пути как раз к тому моменту, когда по расписанию он уже должен был быть в селе. Автобусу не удастся наверстать упущенное время.
3. 1 способ. Разобьём фонари на 25 шестёрок подряд стоящих, и докажем, что в каждой из них был починеный фонарь. Предположим, что в какой-то шестёрке ни один фонарь не был починен. В такой шестёрке не менее двух разбитых фонарей (поскольку в каждой из двух троек, составляющих шестёрку, был разбитый фонарь), между которыми не менее трёх работающих фонарей (так как иначе можно будет указать четыре фонаря, среди которых хотя бы два разбитых). Но как раз трёх работающих фонарей подряд стоять и не может.
2 способ Посмотрим на фонари до прихода электрика. В каждой тройке подряд стоящих фонарей есть хотя бы один испорченный, значит всего испорченных фонарей не менее 50. Пронумеруем первые 50 испорченных фонарей слева направо и разобьём на пары: 1-й со 2-м, 3-й с 4-м, и т.д. (всего 25 пар) Между фонарями одной пары все фонари целые, а значит их не более двух. Поэтому один из испорченных фонарей, входящих в одну пару, надо починить.
4. 552/(1- 
)=564 монеты осталось перед тем как взяли 1/47 часть. 564/ (1 -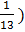 
= 611 монет было первоначально.
5. Площадь прямоугольника, в который вписан треугольник, равна 11∙ 6 = 66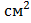 
. Чтобы получить площадь треугольника, нужно из площади прямоугольника вычесть площади трех прямоугольных треугольников. Их площади равны половинам площадей прямоугольников. Площадь одного будет равна (5∙8):2 = 20 
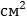, второго – (3∙ 6):2 = 9 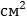, третьего – (1∙11): 2 = = 5,5 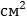. Тогда площадь искомого треугольника будет равна 66 – (20 + 9 + 5,5) = 31,5 .
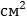Ответы и решения
Класс
Каждое задание оценивается в 10 баллов, максимальное количество баллов – 50
1. 592
2. 
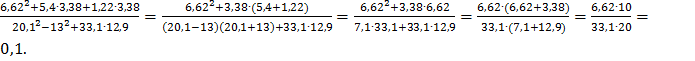
0,1 --------- 2,5%
Х --------- 100%
Х= 4.
3. 
-- число, следующее за числом 12921, которое одинаково читается в обоих направлениях. Тогда скорость автомобиля будет равна (13131 – 12921): 2 = 105 км/ч.
4. Ответ: Алексей получил «5», Борис – «4», Василий – «3».
Рассмотрим три случая.
1 случай. Пусть учитель сказал верно Алексею. Значит, у Алексея – «4». Т.к. Борису и Василию учитель назвал неверные отметки, то у Бориса – «4», а у Василия – «5». Получилось, что у двух учеников оказались одинаковые отметки, что противоречит условию задачи. Данный случай невозможен.
2 случай. Пусть учитель сказал верно Василию. Тогда у Василия отметка – не «5». Т.к. учитель сказал неверно об отметках Алексея и Бориса, то у Алексея отметка не «4», а у Бориса – «4». Тогда у Алексея – «5», у Василия – «3».
3 случай. Пусть учитель сказал верно Борису. Тогда Борис получил не «4». Т.к. утверждения про отметки Алексея и Василия ложные, то у Алексея – не «4», у Василия – «5». Получается, что отметку «4» никто не получил. Этот случай тоже противоречит условию задачи.
5. Треугольники BDE, DEF, EFC, FCA – равнобедренные. Обозначим < DВE=х. …получим х=200. < В=200, <А = <С =800.