Механика микро- и нанодисперсных сред (Ч.2)
Под уравнением магнитного состояния понимают аналитическую зависимость намагниченности вещества от напряженности магнитного поля и температуры, т.е. M(H,T).
В связи с частым использованием ланжевеновской модели намагничивания при анализе различных процессов, протекающих в магнитных жидкостях, приведем вывод уравнения магнитного состояния парамагнитного газа (P. Langevin. 1905 г.).
. (8.8)
Выражение в скобках называется функцией Ланжевена и обозначается L(ξ).
Таким образом, теория приводит к закону намагничивания, описываемому функцией Ланжевена:
М = n 
L(ξ), L(ξ)=cth ξ- 
, 
. (8.9)
Тепловые флуктуации обусловливают стохастические повороты магнитного момента относительно направления поля. Влияние этого механизма на ориентацию магнитного момента определяется ланжевеновским аргументом ξ. Условной границей между «слабыми» и «сильными» магнитными полями применительно к МЖ может служить величина НТ=k0Т/μ0m*, введенная из условия ξ =1.
Приведем оценку НT. Для частиц магнетита с характерным объемом Vf =5·10‑23 м3 магнитный момент m*=MsVf =2,25·10‑19 А·м2. При энергии k0Т =4,15·10‑21 Дж находим HT =1,46·104 А/м.
При Н >> НТ – сильные поля.
При Н << НТ – слабые поля.
С ростом напряженности магнитного поля кривая L(ξ) асимптотически приближается к единице, что соответствует намагниченности насыщения среды МS=n , т.е. полной ориентации магнитных моментов всех частиц вдоль поля. В сильных магнитных полях, когда Н>>k0T/m0 , уравнение (8.9) принимает вид:
, (8.10)
где МS0 – намагниченность насыщения диспергированного ферромагнетика; R –радиус феррочастиц.
В слабых полях при разложении уравнения Ланжевена в ряд Тейлора получаем
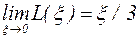, (8.11)
и, следовательно, начальная магнитная восприимчивость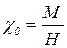 
не зависит от напряженности поля
. (8.12)
Из выражений (8.10) и (8.12) следует, что суперпарамагнетизм МЖ интересен не только как специфическое магнитное явление, но и как неразрушающий метод определения размеров и магнитного момента диспергированных в коллоиде магнитных наночастиц.
Численное значение начальной магнитной восприимчивости концентрированной МЖ (объемная концентрация магнетита ~0,2) при комнатной температуре достигает ~10, что в ~104 раз превышает восприимчивость обычных жидкостей.
С повышением температуры значение χ0 уменьшается. При приближении температуры к точке Кюри Тk магнетика, из которого приготовлен коллоид, его спонтанная намагниченность тоже проявляет заметную зависимость от температуры. Нагревая МЖ выше Тk, можно существенно уменьшить её магнитную восприимчивость, что лежит в основе явления термомагнитной конвекции. Слои МЖ с Т<Тk обладают большей магнитной восприимчивостью и втягиваются в области с большей напряжённостью магнитного поля, вытесняя слои с Т>Тk. Термомагнитная конвекция по интенсивности может во много раз превосходить гравитационную конвекцию.
Восприимчивость возрастает позакону Кюри-Вейсапри понижении температуры Т, однако это увеличение происходит не беспредельно и при некоторой температуре Tg наблюдается максимум зависимости χ0(Т) и последующее уменьшение χ0. Численное значение Tg не связано с температурой затвердевания жидкости-носителя, а зависит от концентрации φ магнитного вещества МЖ и частоты измерительного поля. Система взаимодействующих магнитных диполей – однодоменных коллоидных частиц при понижении температуры образует хаотическую структуру сложным образом перепутанных и разветвлённых дипольных цепочек. Так, при T>Tg МЖ являются жидкими суперпарамагнетиками, а при T<Tg переходят в неупорядоченное гелеобразное состояние.
Из уравнения (8.9) следует, что в небольших интервалах изменения температуры, напряженности магнитного поля, концентрации равновесное значение намагниченности сжимаемой МЖ Ме можно представить в виде линейной зависимости:
, (8.13)
где М0, 
, 
, 
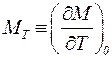– относятся к невозмущенной среде.
В уравнении (8.13) отсутствует член, ответственный за тепловое расширение. Дело в том, что колебания температуры δТ в рассматриваемом случае являются следствием адиабатного характера деформации 
. При этом среда в условиях всестороннего сжатия не испытывает тепловое расширение (скачок температуры в среде при абсолютно жесткой стенке сосуда).
Наряду с МН используется также понятие «полной» или «интегральной» магнитной восприимчивости χ=М/H.
Кривая намагничивания
Для нахождения магнитных параметров χ и Ms баллистическим методом снимается кривая намагничивания M(H). При этом МЖ заполняет ампулу цилиндрической формы, длина которой значительно превосходит диаметр, что позволяет пренебречь размагничивающим полем. Приведем пример обработки кривой намагничивания.
Таблица 3.1.
| Образец | ρ, кг/м3 | φ, % | χ | Ms, кА/м | m*max∙1019, А∙м2 | m*min∙1019, А∙м2 | dmax, нм | dmin, нм |
| МЖ-01 | 3,4 | 45,8 | 7,52 | 2,74 | 14,6 | 10,4 |
В таблице 3.1. представлены физические параметры исследуемого образца МЖ-01, представляющего собой коллоидный раствор магнетита в керосине. В таблице использованы обозначения плотности – ρ, концентрации твердой фазы – φ, начальной магнитной восприимчивости – χ, намагниченности насыщения – Ms. Все параметры определены при температуре 31°С.
Полученная кривая намагничивания МЖ приведена на рисунке 3.2. В соответствии с функцией Ланжевена (L(ξ)=cth ξ - , М = n L(ξ), ) намагниченность насыщения достигается при ξ ~ 10. Представив кривую намагничивания в более крупном масштабе, можно убедиться, что ее начальеый участок действительно является прямолинейным. Начальная магнитная восприимчивость χ определяется по наклону начального участка кривой M(H).
Для нахождения намагниченности насыщения Ms, т.е. значения намагниченности образца при очень большой («насыщающей») напряженности магнитного поля Н на практике поступают следующим образом. В окрестности значений Н-1 ≈ 0 методом линейной аппроксимации зависимости М (Н-1) получают прямолинейный отрезок, экстраполяцией кторого до пересечения с осью ординат находят искомое значение Ms (рисунок 3.3).
5. Пондеромоторная сила
При движении магнитной суспензии в неоднородном магнитном поле на каждую частицу с магнитным моментом 
действует сила [1]
. (2.49)
Движение непроводящей МЖ изменяется под действием объемной магнитной силы:
, (2.50)
которая получена из (2.49) путем суммирования: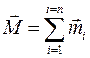 
- намагниченность системы частиц. Поскольку при не слишком высоких частотах 
, то вместо (2.50) можно записать:
. (2.51)
Уравнение движения принимает вид:
. (2.52)
Для несжимаемой жидкости уравнение движения записывается следующим образом:
. (2.53)
В ряде случаев, например, в акустике, вторым членом в квадратных скобках пренебрегают:
. (2.54)
Напряженность магнитного поля определяется уравнениями магнитостатики: 
; 
.
6. Магнитный скачок давления
На границе раздела двух сред с различной магнитной проницаемостью при включении магнитного поля возникает скачок давлений [11]
, (2.57)
где µ0 – магнитная постоянная, 
- единичный вектор нормали к межфазной поверхности, 
и 
- вектора намагниченности сред (индекс 1 относится к «нижней» среде, 
индекс 2 относится к «верхней» среде).
Давление в среде с большей намагниченностью будет меньше. Если верхней средой является воздух, то внутри магнитной среды (в частности – магнитной жидкости) у плоской границы раздела давление будет меньше по сравнению с атмосферным на величину
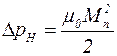, (2.58)
где 
- нормальная к поверхности составляющая намагниченности.
Физическую природу скачка давления можно понять, если учесть, что на границе раздела двух сред происходит скачок нормальной составляющей напряженности магнитного поля:
. (2.59)
Магнитные микро- или наночастицы, расположенные по обе стороны от границы раздела, находятся в различном по величине магнитном поле. В окрестности границы раздела существует неоднородное магнитное поле, градиент которого направлен из среды с большей намагниченностью в среду с меньшей намагниченностью, поскольку в среде с меньшей намагниченностью напряженность магнитного поля больше. На частицу действует сила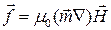 
, направленная в сторону менее магнитной среды, в частности, в атмосферу, что снижает давление в МЖ.
Одним из проявлений магнитного скачка давлений является неустойчивость поверхности МЖ в нормальном к ней магнитном поле. Эта неустойчивость заключается в том, что при достижении определенной критической величины напряженности магнитного поля (определенной намагниченности) поверхность жидкости приобретает специфическую игольчатую форму (сеть конусообразных пиков). Появление пиков связано с тем, что сравнительно небольшое возмущение гладкой поверхности МЖ приводит к искажению магнитного поля, которое вызывает их дальнейший рост.
Примером появления конусообразных пиков на поверхности МЖ может служить фотография поверхности магнитожидкостной перемычки, образованной в неоднородном поле кольцевого магнита [1]. Капля МЖ, внесенная в область максимального поля в трубке, перекрывает ее сечение. При этом магнитное поле перпендикулярно к свободной поверхности перемычки.
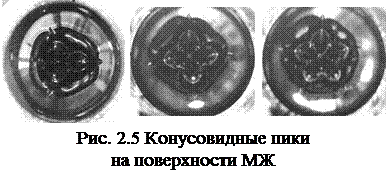По обе стороны перемычки образуются конусовидные пики, обусловленные неустойчивостью поверхности МЖ в поперечном поле. По нашим наблюдениям может образоваться от одного до пяти приблизительно одинаковых пиков, высота которых составляет 1-2 мм. На рис. 2.5 показаны фотографии поверхности магнитожидкостной перемычки.