4.1.1. Свободные колебания линейных механических систем
с одной степенью свободы.
В этом случае зависимость кинетической энергии от обобщенной скорости приводится к виду
, (11)
а зависимость потенциальной энергии 
от обобщенной координаты к виду
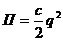. (12)
Коэффициент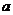 
называют обобщенным коэффициентом инерции, а 
- обобщенным коэффициентом жесткости.
Воспользовавшись, например, уравнениями Лагранжа второго рода, можно получить дифференциальное уравнение движения в виде
; либо 
; (13)
где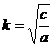 
Дополняя это уравнение начальными условиями 
, будем иметь полную математическую модель для отыскания закона движения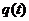 
.
Виды решения этого дифференциального уравнения общеизвестны:
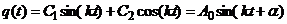, (14)
здесь 
либо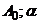 
– постоянные интегрирования.
При заданных начальных условиях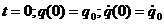 
первый вид решения из (14) будет
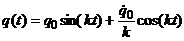, (15)
для второго вида решения постоянная A 0 является амплитудой колебаний и равна
,
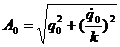начальная фаза колебаний
.
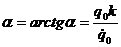Как видно, величина 
имеет смысл частоты свободных колебаний (число колебаний за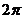 
единиц времени); она связана с периодом 
этих колебаний соотношением 
.
В случае приложения сил линейно-вязкого сопротивления 
уравнение движения примет вид
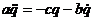либо 
(16)
Здесь 
и 
.
Для действительных значений параметра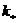 
, когда 
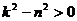(малое сопротивление), при 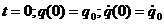получается следующее решение:
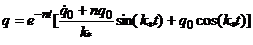(17)
Иная форма записи, содержащая амплитуду 
и начальную фазу 
, имеет вид
; 
;
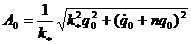(18)
Движение системы с линейно-вязким сопротивлением, строго говоря, не является периодическим и с течением времени затухает.
При малом сопротивлении локальные максимумы отклонений 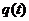повторяются через равные интервалы времени 
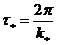(см. рис. 7).
Рис. 7
Удобной характеристикой затухания является логарифмический декремент, представляющий собой натуральный логарифм отношения любых двух последовательных локальных максимумов 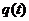и 
:
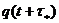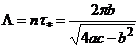(19)
Для критического значения демпфирования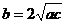 
(или 
) решение уравнения (16) имеет вид
,
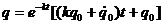а движение утрачивает колебательный характер.
При больших значениях коэффициента сопротивления, когда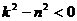 
, решение 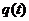представляет сумму экспонент в отрицательных степенях, т.е. колебательное движение отсутствует.
4.1.2. Свободные колебания линейных механических систем
с двумя степенями свободы.
В этом случае зависимость кинетической энергии от обобщенных скоростей приводится к виду
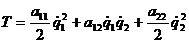, (20)
а зависимость потенциальной энергии от обобщенных координат к виду
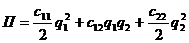(21)
здесь коэффициенты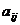 
- обобщенные коэффициенты инерции, а 
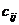– обобщенные коэффициенты жесткости.
Воспользовавшись, например, уравнениями Лагранжа второго рода, можно получить систему дифференциальных уравнений вида
(22)
Отметим, что в линейных консервативных системах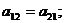 
.
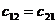Будем искать решение в форме
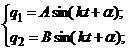(23)
где 
- неизвестные постоянные.
Продифференцируем искомые выражения для обобщенных координат по времени дважды, подставим их в (22). Для удовлетворения этих равенств при любых 
, должны быть равны нулю коэффициенты при 
, т.е. выполняться равенства
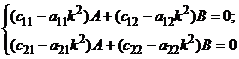. (24)
Система линейных однородных уравнений относительно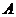 
и 
имеет решение, отличное от нуля, в случае равенства нулю ее определителя
.
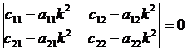Раскрывая определитель, получим уравнение относительно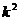 
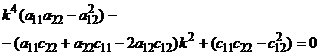(25)
Уравнение (25) называется уравнением частот или вековым уравнением. Оба корня этого уравнения вещественны и положительны. Извлечем из них корни и воспользуемся только положительными значениями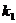 
и 
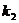, которые называются частотами главных колебаний. Теперь вид (23) будет
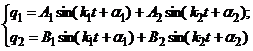
Между числами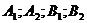 
есть связь. Установим ее, используя любое из уравнений (24), например, первое. Тогда
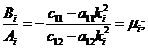
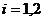. (26)
Каждому значению частоты 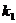и 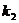отвечают соответствующие значения 
и 
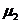, которые называются коэффициентами форм главных колебаний. Вычислив их, найдем
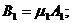
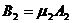(27)
Коэффициенты и 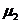имеют простой физический смысл – они показывают, во сколько раз амплитуда соответствующего главного колебания по одной из обобщенных координат больше (или меньше) амплитуды другой.
Теперь решение (23) примет вид
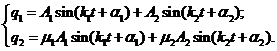(28)
В этом решении частоты 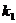, 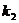и коэффициенты , 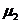- известные числа (они рассчитываются по инерционно – жесткостным характеристикам механической системы), а 
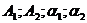- постоянные интегрирования, которые следует определить из начальных условий. Задание четырех начальных условий (при 
), позволяет определить четыре неизвестные величины (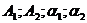), содержащиеся в (28).
Очевидно, что учет линейно-вязкого сопротивления приведет к уже обсужденным выше результатам: при отрицательных действительных корнях частотного уравнения движение будет носить характер экспоненциального убывания, при комплексно-сопряженных корнях будут иметь место затухающие колебания.
В заключение отметим, что методы получения и интегрирования дифференциальных уравнений для линейных механических систем с двумя степенями свободы около положения устойчивого равновесия без всяких изменений могут быть распространены на линейные механические системы с большим числом степеней свободы.
Примеры решения заданий
4.2.1. Положение равновесия линейной механической системы
с одной степенью свободы
Механическая система, состоящая из груза, двух соосных (насаженных неподвижно на единую ось) блоков и диска, прикрепленных к земле пружиной и демпфером (см. рис. 8), находится в положении статического равновесия. Зная жесткость пружины , веса груза и диска, а так же радиусы блоков и диска, определить удлинение пружины.
Рис. 8
РЕШЕНИЕ
1. Рассматриваемая механическая система обладает одной степенью свободы.
2. Заменим действие пружины силой упругости 
, где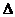 
- удлинение пружины в положении статического равновесия механической системы. Сила со стороны демпфера 
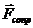, пропорциональная скорости движения его поршня, при покое системы отсутствует.
3. Дадим системе возможное перемещение и запишем выражение для суммы работ всех действующих сил на возможных перемещениях точек их приложения; вынесем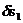 
за общую скобку, сумму работ приравняем к нулю. Тогда
.
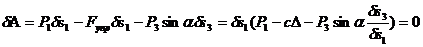При получении выражения учтено, что элементарная работа силы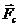 
равна нулю, так как сила приложена в мгновенном центре скоростей колеса 3.
4. Запишем уравнения связей, используя соотношения кинематики:
;
;
.
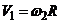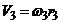Для рассматриваемой механической системы возможные перемещения пропорциональны соответствующим скоростям, т.е. справедливы соотношения
; 
.
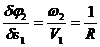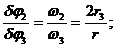
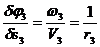5. Приравняв нулю выражение в круглых скобках, получим выражение для расчета удлинения пружины в положении статического равновесия механической системы: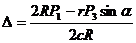 
.
4.2.2. Дифференциальное уравнение движения
механической системы с одной степенью свободы
Используя уравнения Лагранжа второго рода получить дифференциальное уравнение движения груза. Осевой момент инерции соосных блоков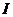 
и коэффициент 
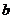силы сопротивления демпфера полагать заданным.
РЕШЕНИЕ
1. На рис. 8 изображена механическая система и внешние силы, на нее действующие.
2. Выберем за обобщенную координату линейное перемещение первого груза. Уравнения кинематических связей останутся прежними:
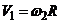или 
;
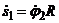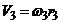или 
;
или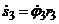 
.
При записи учтено, что нити не растяжимы, а мгновенный центр скоростей диска, катящегося без скольжения, расположен в точке его соприкосновения с плоскостью.
3. Составим выражение для кинетической энергии механической системы:
.
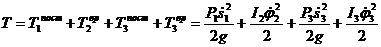4. Вынесем за скобки квадрат обобщенной скорости (скорости груза)
.
При получении результата учтено, что осевой момент инерции однородного диска 
.
5. Частная производная от кинетической энергии по обобщенной координате будет равна нулю, так как полученное выражение от обобщенной координаты не зависит.
Частная производная от кинетической энергии по обобщенной скорости будет
.
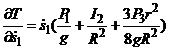6. Производная по времени от частной производной кинетической энергии по обобщенной скорости будет
.
7. Для вычисления обобщенной силы дадим системе возможное перемещение. Составим сумму работ всех внешних сил на соответствующих возможных перемещениях и вынесем возможное перемещение по обобщенной координате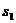 
за скобки:
Выражение в квадратных скобках и есть обобщенная сила для возможного перемещения по выбранной обобщенной координате (при записи учтено условие равновесия механической системы, полученное при решении предыдущего примера).
8. После подстановки в уравнения Лагранжа второго рода выражений для частных производных и обобщенной силы, окончательно имеем
.
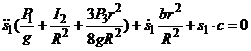Структура полученного уравнения совпадает с (16), решение которого обсуждено выше.
В случае необходимости определить законы движения других элементов механической системы следует воспользоваться уравнениями кинематических связей.
4.2.3. Равновесие линейной механической системы
с двумя степенями свободы
Механическая система, состоящая из однородного диска, двух соосных (насаженных неподвижно на единую ось) блоков и груза, прикрепленного к земле пружиной (см. рис. 9), находится в положении статического равновесия. Зная жесткости пружин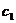 
и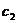 
, веса грузов и радиусы блоков, определить удлинения пружин в положении равновесия.
Рис. 9
РЕШЕНИЕ
1. Рассматриваемая механическая система обладает двумя степенями свободы.
2. В качестве независимых обобщенных координат выберем линейные перемещения груза 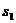и центра диска 
. Заменим действие первой пружины силой упругости 
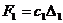, где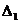 
- удлинение пружины в положении статического равновесия механической системы, а второй - внутренней силой 
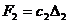, где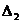 
- удлинение второй пружины.
3. Дадим системе возможное перемещение 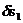по первой обобщенной координате, положив равным нулю возможное перемещение по второй обобщенной координате (т.е. 
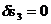). Запишем для этого случая выражение суммы работ всех действующих на систему сил и приравняем ее к нулю (так как диск остается неподвижным, действующие на него силы работу не совершают). Вынесем 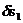за общую скобку. Тогда
,
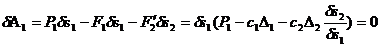где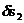 
– возможное перемещение в точке приложения силы 
.
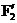4. Запишем уравнения связей, используя соотношения кинематики:
;
.
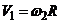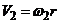Для рассматриваемой механической системы возможные перемещения пропорциональны соответствующим скоростям, т.е. справедливы соотношения
; 
.
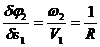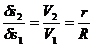5. Приравняв нулю выражение в круглых скобках, получим первое уравнение для расчета статического удлинения пружин:
.
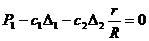6. Теперь дадим системе возможное перемещение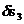 
по второй обобщенной координате, положив равным нулю возможное перемещение по первой обобщенной координате (т.е. 
). Запишем для этого случая выражение суммы работ всех действующих на систему сил и приравняем ее к нулю (так как груз и соосный блок остаются неподвижными, действующие на них силы работу не совершают). Вынесем 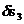за общую скобку. Тогда
,
где 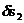- возможное перемещение в точке приложения силы 
.
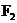7. Запишем уравнения связей, используя соотношения кинематики:
;
.
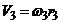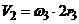Для рассматриваемой механической системы возможные перемещения пропорциональны соответствующим скоростям, т.е. справедливо соотношение
.
8. Приравняв нулю выражение в круглых скобках, получим второе уравнение для расчета статического удлинения пружин:
.
Решив систему алгебраических уравнений относительно удлинений пружин, получим
; 
.
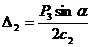4.2.4. Свободные колебания линейной механической системы
с двумя степенями свободы
Для механической системы, изображенной на рис. 9, получить дифференциальные уравнения движения, воспользовавшись уравнениями Лагранжа второго рода. Составить выражения для вычисления частот и форм главных колебаний. Осевой момент инерции соосных блоков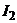 
полагать заданным.
РЕШЕНИЕ
1. Рассматриваемая механическая система обладает двумя степенями свободы.
2. В качестве независимых обобщенных координат выберем линейные перемещения груза 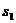и центра диска . Заменим действие первой пружины силой упругости 
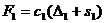, где 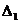- удлинение пружины в положении статического равновесия механической системы, а второй - внутренней силой 
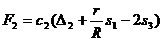, где 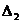- удлинение второй пружины, а 
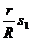и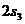 
- перемещения левого и правого концов второй пружины, выраженные через выбранные обобщенные координаты (см. уравнения кинематических связей).
3. Для составления уравнений Лагранжа второго рода (9) сначала получим выражения для обобщенных сил, воспользовавшись следующей формулой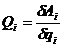 
.
4. Дадим системе возможное перемещение 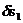по первой обобщенной координате, положив равным нулю возможное перемещение по второй обобщенной координате (т.е. 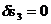). Запишем для этого случая выражение суммы работ всех действующих на систему сил (так как диск остается неподвижным, действующие на него силы работу не совершают). Вынесем 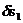за общую скобку. Тогда
,
где 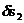- возможное перемещение в точке приложения силы .
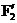5. Запишем уравнения связей, используя соотношения кинематики:
;
.
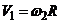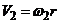Для рассматриваемой механической системы возможные перемещения пропорциональны соответствующим скоростям, т.е. справедливы соотношения
; .
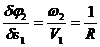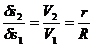6. Выражение в квадратных скобках является обобщенной силой, соответствующей первой обобщенной координате; учитывая соответствующее уравнение равновесия, получим для нее следующее выражение:
.
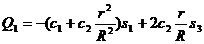7. Теперь дадим системе возможное перемещение 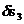по второй обобщенной координате, положив равным нулю возможное перемещение по первой обобщенной координате (т.е. ). Запишем для этого случая выражение суммы работ всех действующих на систему сил (так как груз и соосный блок остаются неподвижными, действующие на них силы работу не совершают). Вынесем 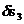за общую скобку. Тогда
,
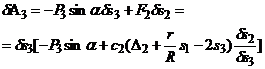где 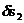- возможное перемещение в точке приложения силы .
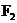8. Запишем уравнения связей, используя соотношения кинематики:
;
.
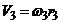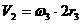Для рассматриваемой механической системы возможные перемещения пропорциональны соответствующим скоростям, т.е. справедливо соотношение
.
9. Выражение в квадратных скобках является обобщенной силой, соответствующей первой обобщенной координате; учитывая соответствующее уравнение равновесия, получим для нее следующее выражение:
.
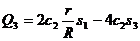10. Теперь составим выражение для кинетической энергии механической системы:
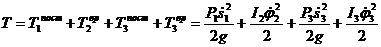
11. Запишем уравнения кинематических связей:
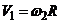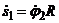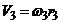или ;
или .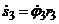
12. Тогда выражение для кинетической энергии можно привести к виду
.
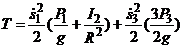При получении результата учтено, что осевой момент инерции однородного диска .
13. Продифференцировав выражение для кинетической энергии по обобщенным координатам, скоростям и по времени, получим слагаемые для левых частей уравнений Лагранжа второго рода:
.
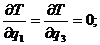
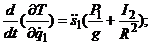
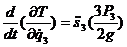14. Подставим все полученные выражения в уравнения Лагранжа второго рода:
.
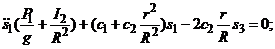
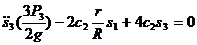15. Заметим, что система уравнений приводится к виду (22) при 
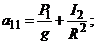
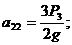
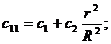
16. Зная все обобщенные коэффициенты инерции и жесткости, составляем уравнение частот (25). Найдя его корни (частоты главных колебани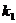й) и 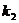, по формулам (26) определяем коэффициенты форм главных колебаний и 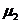. Найденные значения позволяют записать выражения для законов изменения обобщенных координат в форме (28). Задание четырех начальных условий: при 
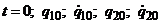, позволяет определить четыре неизвестные величины (
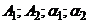), содержащиеся в (28).
Список литературы
1. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики: Учебник. – М.: Лань, 2009.
2. Сборник заданий для курсовых работ по теоретической механике: учебное пособие./ коллектив авторов: под общ. ред. А.А. Яблонского – 18-е изд., стер. – М.: Кнорус, 2011.
3. Мелконян А.Л., Черныш А.А. Основы аналитической механики. Колебания линейных механических систем. Учебное пособие. Издательство СПбГМТУ, СПб, 2010 г.
4. Мелконян А.Л., Черныш А.А. Теоретическая механика. Часть 3. Конспект лекций. Учебное пособие, Издательство СПбГМТУ, СПб, 2014 г.
5. Мелконян А. Л., Николаев И. А., Титова Ю. Ф. Рекомендации для выполнения расчетно-графических работ по теоретической механике. Часть 2. Учебное пособие, Издательство СПбГМТУ, СПб, 2015 г.
[1] Рассматривается та же механическая система, что и в учебном пособии [5], в которой исключено влияние демпфера.