ВЕКТОРНАЯ АЛГЕБРА
методические указания
и индивидуальные задания
к практическим занятиям
по математике
для студентов всех специальностей
института транспорта
очной формы обучения
Тюмень 2003
Утверждено редакционно–издательским советом
Тюменского государственного нефтегазового университета
Составители: Бакановская Н.Н., ассистент
Редактор: Скалкина М.А., к.ф.–м.н., профессор
© государственное образовательное учреждение высшего профессионального образования
«Тюменский государственный нефтегазовый университет»
Предлагаемая работа предназначена помочь студентам, изучающим векторную алгебру, получить навыки решения стандартных задач.
Перед выполнением индивидуальных заданий рекомендуем ознакомиться с решением заданий нулевого варианта, изложенных в данных методических указаниях.
З а д а н и е 1. Написать разложение вектора  по векторам
по векторам  ,
,  ,
,  , если
, если  ,
,  ,
,  ,
,  .
.
Р е ш е н и е. Запишем вектор  в виде линейной комбинации векторов
в виде линейной комбинации векторов  ,
,  и
и  :
:  . Найдем коэффициенты
. Найдем коэффициенты  ,
,  ,
,  . Для этого запишем разложение вектора
. Для этого запишем разложение вектора  в координатной форме:
в координатной форме:

Подставим координаты заданных векторов. Получим систему

решив которую, найдем коэффициенты  . Т.е.
. Т.е.  .
.
З а д а н и е 2. Найти угол между векторами  и
и  , если
, если  ,
,  ,
,  ,
,  .
.
Р е ш е н и е. Воспользуемся формулой  . Определим координаты векторов
. Определим координаты векторов  и
и  , при этом учтем, что при умножении вектора на число, мы умножаем на это число каждую координату этого вектора, а при сложении векторов – складываем одноименные координаты:
, при этом учтем, что при умножении вектора на число, мы умножаем на это число каждую координату этого вектора, а при сложении векторов – складываем одноименные координаты:  ,
,  .
.
Найдем скалярное произведение векторов  и
и  и их длины.
и их длины.  ,
,  ,
,  . Подставив в формулу, получим
. Подставив в формулу, получим  . Отсюда
. Отсюда  .
.
З а д а н и е 3. Найти проекцию вектора  на вектор
на вектор  , если
, если  ,
,  ,
,  .
.
Р е ш е н и е. Проекция вектора  на вектор
на вектор  находится по формуле
находится по формуле  . Определим координаты векторов
. Определим координаты векторов  и
и  , их скалярное произведение и длину вектора
, их скалярное произведение и длину вектора  :
:  ,
,  ,
,  ,
,  . Тогда
. Тогда  .
.
З а д а н и е 4. Вычислить площадь параллелограмма, построенного на векторах  и
и  , если
, если  ,
,  .
.
Р е ш е н и е.
 Площадь параллелограмма будем искать по формуле
Площадь параллелограмма будем искать по формуле  . Для этого найдем сначала координаты векторов
. Для этого найдем сначала координаты векторов  и
и  , а затем их векторное произведение.
, а затем их векторное произведение.  ,
,  ,
,
 .
.
Вычислим модуль полученного векторного произведения, который и будет численно равен искомой площади параллелограмма: 
З а д а н и е 5. Параллелограмм построен на векторах  и
и  , где
, где  ,
,  ,
,  ^
^  . Вычислить длину диагоналей этого параллелограмма, угол между диагоналями и площадь параллелограмма.
. Вычислить длину диагоналей этого параллелограмма, угол между диагоналями и площадь параллелограмма.
Р е ш е н и е.

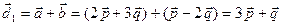 ,
,  ,
,

 Угол между диагоналями обозначим буквой
Угол между диагоналями обозначим буквой  , тогда
, тогда

Следовательно, 

З а д а н и е 6. Компланарны ли векторы  ,
,  ,
,  ?
?
Р е ш е н и е. Если векторы компланарны, то их смешанное произведение равно нулю. Проверим это. Найдем смешанное произведение данных векторов:
 векторы некомпланарны.
векторы некомпланарны.
З а д а н и е 7. Точки  являются вершинами пирамиды. Вычислить ее объем, площадь грани
являются вершинами пирамиды. Вычислить ее объем, площадь грани  и высоту пирамиды, опущенную на эту грань.
и высоту пирамиды, опущенную на эту грань.
Р е ш е н и е. Объем пирамиды будем  искать по формуле
искать по формуле  , где
, где  ,
,  и
и  –векторы, совпадающие с ребрами пирамиды. В нашем случае такими векторами будут
–векторы, совпадающие с ребрами пирамиды. В нашем случае такими векторами будут  .
.
Найдем координаты этих векторов, а затем их смешанное произведение.


Теперь найдем площадь грани  по формуле
по формуле  .
.
 . Тогда площадь грани будет равна
. Тогда площадь грани будет равна 
Т.к.  , то высота H =
, то высота H =  , опущенная на грань
, опущенная на грань  , равна
, равна  .
.
З а д а н и е 8. Найти вектор  , перпендикулярный к векторам
, перпендикулярный к векторам  и
и  и удовлетворяющий условию
и удовлетворяющий условию  .
.
Р е ш е н и е. Пусть вектор  имеет координаты
имеет координаты  . Т. к. вектор
. Т. к. вектор  перпендикулярен векторам
перпендикулярен векторам  и
и  , то
, то  . Запишем все три скалярных произведения в координатной форме:
. Запишем все три скалярных произведения в координатной форме:

Решив полученную систему, получим, что  .
.
З а д а н и е 9. Зная векторы 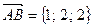 и
и  , совпадающие с двумя сторонами треугольника, найти угол при вершине
, совпадающие с двумя сторонами треугольника, найти угол при вершине  и площадь треугольника.
и площадь треугольника.
Р е ш е н и е. Угол при вершине  – это угол между векторами
– это угол между векторами 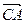 и
и  . Вектор
. Вектор  , тогда
, тогда  ,
,
отсюда  .
.
Теперь найдем площадь треугольника:  ,
,  .
.
З а д а н и е 10. Сила  приложена к точке
приложена к точке 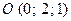 . Определить момент этой силы относительно точки
. Определить момент этой силы относительно точки  .
.
Р е ш е н и е. Момент силы  относительно точки
относительно точки  есть вектор
есть вектор  . Найдем координаты вектора
. Найдем координаты вектора  и искомого вектора
и искомого вектора  :
:  ,
,  , т.е.
, т.е.  .
.
Индивидуальные задания по векторной алгебре
Задание 1. Написать разложение вектора  по векторам
по векторам  ,
,  ,
,  .
.
1.  ={15; –20; –1},
={15; –20; –1},  ={0; 2; 1},
={0; 2; 1},  ={0; 1; –1},
={0; 1; –1},  ={5; –3; 2}.
={5; –3; 2}.
2.  ={2; 7; 5},
={2; 7; 5},  ={1; 0; 1},
={1; 0; 1},  ={1; –2; 0},
={1; –2; 0},  ={0; 3; 1}.
={0; 3; 1}.
3.  ={8; –7; –13},
={8; –7; –13},  ={0; 1; 5},
={0; 1; 5},  ={3; –1; 2},
={3; –1; 2},  ={–1; 0; 1}.
={–1; 0; 1}.
4.  ={0; –8; 9},
={0; –8; 9},  ={0; –2; 1},
={0; –2; 1},  ={3; 1; –1},
={3; 1; –1},  ={4; 0; 1}.
={4; 0; 1}.
5.  ={ –13; 2; 18},
={ –13; 2; 18},  ={1; 1; 4},
={1; 1; 4},  ={–3; 0; 2},
={–3; 0; 2},  ={1; 2; –1}.
={1; 2; –1}.
6.  ={11; –1; 4},
={11; –1; 4},  ={1; –1; 2},
={1; –1; 2},  ={3; 2; 0},
={3; 2; 0},  ={–1; 1; 1}.
={–1; 1; 1}.
7.  ={–1; 7; 0},
={–1; 7; 0},  ={0; 3; 1},
={0; 3; 1},  ={1; –1; 2},
={1; –1; 2},  ={2; –1; 0}.
={2; –1; 0}.
8.  ={3; 1; 3},
={3; 1; 3},  ={2; 1; 0},
={2; 1; 0},  ={1; 0; 1},
={1; 0; 1},  ={4; 2; 1}.
={4; 2; 1}.
9.  ={23; –14; –30},
={23; –14; –30},  ={2; 1; 0},
={2; 1; 0},  ={1; –1; 0},
={1; –1; 0},  ={–3; 2; 5}.
={–3; 2; 5}.
10. = {8; 9; 4},  = {1; 0; 1},
= {1; 0; 1},  ={0; –2; 1},
={0; –2; 1},  ={1; 3; 0}.
={1; 3; 0}.
11.  ={–15; 5; 6},
={–15; 5; 6},  ={0; 5; 1},
={0; 5; 1},  ={3; 2; –1},
={3; 2; –1},  ={–1; 1; 0}.
={–1; 1; 0}.
12.  ={–5; 9; –13},
={–5; 9; –13},  ={0; 1; –2},
={0; 1; –2},  ={3; –1; 1},
={3; –1; 1},  ={4; 1; 0}.
={4; 1; 0}.
13.  ={–9; –8; –3},
={–9; –8; –3},  ={1; 4; 1},
={1; 4; 1},  ={–3; 2; 0},
={–3; 2; 0},  ={1; –1; 2}.
={1; –1; 2}.
14.  ={8; 1; 12},
={8; 1; 12},  ={1; 2; –1},
={1; 2; –1},  ={3; 0; 2},
={3; 0; 2},  ={–1; 1; 1}.
={–1; 1; 1}.
15.  ={3; 1; 8},
={3; 1; 8},  ={0; 1; 3},
={0; 1; 3},  ={1; 2; –1},
={1; 2; –1},  ={2; 0; –1}.
={2; 0; –1}.
16.  ={8; 0; 5},
={8; 0; 5},  ={2; 0; 1},
={2; 0; 1},  ={1; 1; 0},
={1; 1; 0},  ={4; 1; 2}.
={4; 1; 2}.
17.  ={11; 5; –3},
={11; 5; –3},  ={1; 0; 2},
={1; 0; 2},  ={–1; 0; 1},
={–1; 0; 1},  ={2; 5; –3}.
={2; 5; –3}.
18.  ={2; –1; 11},
={2; –1; 11},  ={1; 1; 0},
={1; 1; 0},  ={0; 1; –2},
={0; 1; –2},  ={1; 0; 3}.
={1; 0; 3}.
19.  ={5; 15; 0},
={5; 15; 0},  ={1; 0; 5},
={1; 0; 5},  ={–1; 3; 2},
={–1; 3; 2},  ={0; –1; 1}.
={0; –1; 1}.
20.  ={6; –1; 7},
={6; –1; 7},  ={1; –2; 0},
={1; –2; 0},  ={–1; 1; 3},
={–1; 1; 3},  ={1; 0; 4}.
={1; 0; 4}.
21.  ={6; 5; –14},
={6; 5; –14},  ={1; 1; 4},
={1; 1; 4},  ={0; –3; 2},
={0; –3; 2},  ={2; 1; –1}.
={2; 1; –1}.
22.  ={–1; 7; –4},
={–1; 7; –4},  ={–1; 2; 1},
={–1; 2; 1},  ={2; 0; 3},
={2; 0; 3},  ={1; 1; –1}.
={1; 1; –1}.
23.  ={3; 3; –1},
={3; 3; –1},  ={3; 1; 0},
={3; 1; 0},  ={–1; 2; 1},
={–1; 2; 1},  ={–1; 0; 2}.
={–1; 0; 2}.
24.  ={3; –3; 4},
={3; –3; 4},  ={1; 0; 2},
={1; 0; 2},  ={0; 1; 1},
={0; 1; 1},  ={2; –1; 4}.
={2; –1; 4}.
25.  ={–19; –1; 7},
={–19; –1; 7},  ={0; 1; 1},
={0; 1; 1},  ={–2; 0; 1},
={–2; 0; 1},  ={3; 1; 0}.
={3; 1; 0}.
26.  ={13; 2; 7},
={13; 2; 7},  ={5; 1; 0},
={5; 1; 0},  ={2; –1; 3},
={2; –1; 3},  ={1; 0; –1}.
={1; 0; –1}.
27.  ={–5; –5; 5},
={–5; –5; 5},  ={–2; 0; 1},
={–2; 0; 1},  ={1; 3; –1},
={1; 3; –1},  ={0; 4; 1}.
={0; 4; 1}.
28.  ={–9; 5; 5},
={–9; 5; 5},  ={4; 1; 1},
={4; 1; 1},  ={2; 0; –3},
={2; 0; –3},  ={–1; 2; 1}.
={–1; 2; 1}.
29.  ={1; –4; 4},
={1; –4; 4},  ={2; 1; –1},
={2; 1; –1},  ={0; 3; 2},
={0; 3; 2},  ={1; –1; 1}.
={1; –1; 1}.
30.  ={6; 12; –1},
={6; 12; –1},  ={1; 3; 0},
={1; 3; 0},  ={2; –1; 1},
={2; –1; 1},  ={0; –1; 2}.
={0; –1; 2}.
Задание 2. Найти угол между векторами  и
и  , если:
, если:
1.  ={–1; 2; 8},
={–1; 2; 8},  ={3; 7; –1},
={3; 7; –1},  = 4
= 4  – 3
– 3  ,
,  = 9
= 9  – 12
– 12  .
.
2.  ={2; 0; –5},
={2; 0; –5},  ={1; –3; 4},
={1; –3; 4},  = 2
= 2  – 5
– 5  ,
,  = 5
= 5  – 2
– 2  .
.
3.  ={4; 2; –7},
={4; 2; –7},  ={5; 0; –3},
={5; 0; –3},  =
=  – 3
– 3  ,
,  = 6
= 6  – 2
– 2  .
.
4.  ={–1; 3; 4},
={–1; 3; 4},  ={2; –1; 0},
={2; –1; 0},  = 6
= 6  – 2
– 2  ,
,  =
=  – 3
– 3  .
.
5.  ={5; 0; 8},
={5; 0; 8},  ={–3; 1; 7},
={–3; 1; 7},  = 3
= 3  – 4
– 4  ,
,  = 12
= 12  – 9
– 9  .
.
6.  ={2; –1; 6},
={2; –1; 6},  ={–1; 3; 8},
={–1; 3; 8},  = 5
= 5  – 2
– 2  ,
,  = 2
= 2  – 5
– 5  .
.
7.  ={4; 2; 9},
={4; 2; 9},  ={0; –1; 3},
={0; –1; 3},  = 4
= 4  – 3
– 3  ,
,  = 4
= 4  – 3
– 3  .
.
8.  ={9; 5; 3},
={9; 5; 3},  ={7; 1; –2},
={7; 1; –2},  = 2
= 2  –
–  ,
,  = 3
= 3  + 5
+ 5  .
.
9.  ={5; –1; –2},
={5; –1; –2},  ={6; 0; 7},
={6; 0; 7},  = 3
= 3  – 2
– 2  ,
,  = 4
= 4  – 6
– 6  .
.
10.  ={2; –1; 4},
={2; –1; 4},  ={3; –7; –6},
={3; –7; –6},  = 2
= 2  – 3
– 3  ,
,  = 3
= 3  – 2
– 2  .
.
11.  ={3; 7; 0},
={3; 7; 0},  ={4; 6; –1},
={4; 6; –1},  = 3
= 3  + 2
+ 2  ,
,  = 5
= 5  – 7
– 7  .
.
12.  ={1; –2; 4},
={1; –2; 4},  ={7; 3; 5},
={7; 3; 5},  = 6
= 6  – 3
– 3  ,
,  =
=  – 2
– 2  .
.
13.  ={3; –1; 6},
={3; –1; 6},  ={5; 7; 10},
={5; 7; 10},  = 4
= 4  – 2
– 2  ,
,  =
=  – 2
– 2  .
.
14.  ={8; 3; –1},
={8; 3; –1},  ={4; 1; 3},
={4; 1; 3},  = 2
= 2  –
–  ,
,  = 2
= 2  – 4
– 4  .
.
15.  ={5; 0; –2},
={5; 0; –2},  ={6; 4; 3},
={6; 4; 3},  = 5
= 5  – 3
– 3  ,
,  = 6
= 6  – 10
– 10  .
.
16.  ={7; 9; –2};
={7; 9; –2};  ={5; 4; 3},
={5; 4; 3},  = 4
= 4  –
–  ,
,  = 4
= 4  –
–  .
.
17.  ={–1; 2; –1},
={–1; 2; –1},  ={2; –7; 1},
={2; –7; 1},  = 6
= 6  – 2
– 2  ,
,  =
=  – 3
– 3  .
.
18.  ={3; 7; 0},
={3; 7; 0},  ={1; –3; 4},
={1; –3; 4},  = 4
= 4  – 2
– 2  ,
,  =
=  – 2
– 2  .
.
19.  ={–2; 7; –1},
={–2; 7; –1},  ={–3; 5; 2},
={–3; 5; 2},  = 2
= 2  + 3
+ 3  ,
,  = 3
= 3  + 2
+ 2  .
.
20.  ={0; 3; –2},
={0; 3; –2},  ={1; –2; 1},
={1; –2; 1},  = 5
= 5  – 2
– 2  ,
,  = 3
= 3  + 5
+ 5  .
.
21.  ={5; 0; –1},
={5; 0; –1},  ={7; 2; 3},
={7; 2; 3},  = 2
= 2  –
–  ,
,  = 3
= 3  – 6
– 6  .
.
22.  ={1; 4; 2},
={1; 4; 2},  ={3; –2; 6},
={3; –2; 6},  = 2
= 2  –
–  ,
,  = 3
= 3  – 6
– 6  .
.
23.  ={–2; –3; –2},
={–2; –3; –2},  ={1; 0; 5},
={1; 0; 5},  = 3
= 3  + 9
+ 9  ,
,  = –
= –  – 3
– 3  .
.
24.  ={3; 4; –1},
={3; 4; –1},  ={2; –1; 1},
={2; –1; 1},  = 6
= 6  – 3
– 3  ,
,  =
=  – 2
– 2  .
.
25.  ={1; –2; 5},
={1; –2; 5},  ={3; –1; 0},
={3; –1; 0},  = 4
= 4  – 2
– 2  ,
,  =
=  – 2
– 2  .
.
26.  ={1; 4; –2},
={1; 4; –2},  ={1; 1; –1},
={1; 1; –1},  =
=  +
+  ,
,  = 4
= 4  + 2
+ 2  .
.
27.  ={3; 5; 4},
={3; 5; 4},  ={5; 9; 7},
={5; 9; 7},  = – 2
= – 2  +
+  ,
,  = 3
= 3  – 2
– 2  .
.
28.  ={1; 2; –3},
={1; 2; –3},  ={2; –1; –1},
={2; –1; –1},  = 4
= 4  + 3
+ 3  ,
,  = 8
= 8  –
–  .
.
29.  ={–2; 4; 1},
={–2; 4; 1},  ={1; –2; 7},
={1; –2; 7},  = 5
= 5  + 3
+ 3  ,
,  = 2
= 2  –
– 
30. 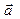 ={1; 0; 1},
={1; 0; 1},  ={–2; 3; 5},
={–2; 3; 5},  =
=  + 2
+ 2  ,
,  = 3
= 3  –
–  .
.
Задание 3. Найти проекцию вектора  на вектор
на вектор  , если:
, если:
1. А (–2; 4; –6), В (0; 2; –4), С (–6;8;–10).
2. А (–4; 0; 4), В (–1; 6; 7), С (1; 10; 9).
3. А (0; 1; 0), В (0; 2; 1), С (1; 2; 0).
4. А (1; 4; –1), В (–2; 4; –5), С (8; 4; 0).
5. А (–2; 1; 1), В (2; 3; –2), С (0; 0; 3).
6. А (3; 3; –1), В (5; 1; –2), С (4;1;–3).
7. А (0; 3; –6), В (9; 3; 6), С (12; 3;3).
8. А (–1;2;–3), В (0;1;–2), С (–3;4;–5).
9. А (2;2;7), В (0;0;6), С (–2;5;7).
10. А (2;3;2), В (–1;–3;–1), С (–3;–7;–3).
11. А (7;0;2), В (7;1;3), С (8;–1;2).
12. А (1; –1;0), В (– 2;– 1;4), С (8;–1;–1).
13. А (– 4;3;0), В (0;1;3), С (–2;4;–2).
14. А (3;3;–1), В (5;1;–2), С (4;1;1).
15. А (0;2;–4); В (8;2;2); С (6;2;4).
16. А (3;–6;9), В (0;–3;6), С (9; –12; 15).
17. А (2;–8;–1), В (4;–6;0), С (–2; –5; –1).
18. А (0;0;4), В (–3;–6;1), С (–5; –10; –1).
19. А (6;2;–3), В (6;3;–2), С (7; 3; –3).
20. А (–1;–2;1), В (–4;–2;5), С (–8; –2; 2).
21. А (2; 1; –1), В (6; –1; –4), С (4; 2; 1).
22. А (3; 3; –1), В (1; 5; –2), С (4;1;1).
23. А (0; 1; –2), В (3; 1; 2), С (4; 1; 1).
24. А (2; –4; 6), В (0; –2; 4), С (6;–8; 10).
25. А (–3; –7; –5), В (0;–1;–2), С (2;3;0).
26. А (5; 3; –1), В (5; 2; 0), С (6;4;–1).
27. А (–4; –2; 0), В (–1; –2; 4), С (3;–2;1).
28. А (–1; 2; –3), В (3; 4; –6), С (1; 1; –1).
29. А (3; 3; –1), В (5;5;–2), С (4; 1; 1).
30. А (0; –3; 6), В (–12; –3; –3), С (–9; –3; –6).
Задание 4. Параллелограмм построен на векторах 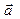 и`
и`  . Вычислить длины диагоналей этого параллелограмма; угол между диагоналями и площадь параллелограмма.
. Вычислить длины диагоналей этого параллелограмма; угол между диагоналями и площадь параллелограмма.
1. 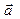 = 3
= 3  + 2
+ 2  ;
;  = 2
= 2  –
–  ; |
; |  | = 4; |
| = 4; |  | = 3; (
| = 3; ( ^
^  ) = 3p/4.
) = 3p/4.
2. 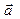 = 2
= 2  – 3
– 3  ;
;  = 5
= 5  +
+  ; |
; |  | = 2; |
| = 2; |  | = 3; (
| = 3; ( ^
^  ) = p/2.
) = p/2.
3. 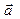 = 2
= 2  + 3
+ 3  ;
;  =
=  – 2
– 2  ; |
; |  | = 2; |
| = 2; |  | = 1; (
| = 1; ( ^
^  ) = p/3.
) = p/3.
4. 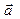 = 6
= 6  –
–  ;
;  = 5
= 5  +
+  ; |
; |  | = 1/2; |
| = 1/2; |  | = 4; (
| = 4; ( ^
^  ) = 5p/6.
) = 5p/6.
5. 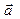 = 3
= 3  – 4
– 4  ;
;  =
=  + 3
+ 3  ; |
; |  | = 2; |
| = 2; |  | = 3; (
| = 3; ( ^
^  ) = p/4.
) = p/4.
6. 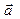 = 5
= 5  –
–  ;
;  =
=  +
+  ; |
; |  | = 5; |
| = 5; |  | = 3; (
| = 3; ( ^
^  ) = 5p/6.
) = 5p/6.
7. 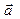 = 3
= 3  +
+  ;
;  =
=  – 3
– 3  ; |
; |  |= 7; |
|= 7; |  | = 2; (
| = 2; ( ^
^  ) = p/4.
) = p/4.
8. 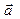 =
=  + 3
+ 3  ;
;  = 3
= 3  –
–  ; |
; |  | = 3; |
| = 3; |  | = 5; (
| = 5; ( ^
^  ) =2p/3.
) =2p/3.
9. 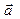 = 7
= 7  +
+  ;
;  =
=