Основные законы алгебры множеств

Практическое занятие

по «Дискретной математике»
Тема: Теория множеств

 

Под множеством понимают любой набор определенных и различимых между собой объектов, мыслимый как единое целое. Объекты, составляющие множество, называются элементами множества.

Если каждый элемент множества А является элементом множества В, то говорят, что А включено в В (обозначение: АÍВ, при этом А – подмножество В).

Два множества называются равными, если они состоят из одних и тех же элементов: (А=В) Û (" x ÎA x ÎB Ù " x ÎB x ÎA) Û (АÍВ Ù BÍA).

Относительным дополнением множества А до множества Х называется множество элементов, принадлежащих Х, но не принадлежащих А: Х\А = { x | x ÎX Ù x ÏA}. Такое множество часто называют разностью или “Х без А”.

Абсолютным дополнением множества А называется множество всех тех элементов, которые не принадлежат А: .

Объединением множеств А и В называется множество АÈВ, элементы которого принадлежат хотя бы одному из этих множеств.

Пересечением множеств А и В называется множество АÇВ, элементы которого принадлежат каждому из этих множеств.

Симметрической разностью множеств А и В называется множество АÄВ, элементы которого принадлежат ровно одному из этих множеств: АÄВ=(А\В)È(В\А).

Диаграммой Венна-Эйлера называется схематическое изображение универсального множества U в виде прямоугольника, а других множеств в виде кругов (круги Эйлера) или какой-то другой области.

Основные законы алгебры множеств

 

1) Коммутативность a) А È В = В È А b) А Ç В = В Ç А c) А Ä В = В Ä А d) А \ В ¹ В \ А	2) Взаимодействие с самим множеством и его дополнением a) А Ç А = А b) А È А = А c) А Ç = Æ d) А È = U
3) Свойства нуля и единицы a) АÇÆ = Æ b) АÈÆ = А c) АÇU = А d) АÈU = U	4) Ассоциативность a) А È (ВÈС) = (АÈВ) È С b) А Ç (ВÇС) = (АÇВ) Ç С c) А Ä (ВÄС) = (АÄВ) Ä С d) А \ (В \ С) ¹ (А \ В) \ С
5) Дистрибутивность a) АÇ(ВÈС)=(АÇВ)È(АÇС) b) АÈ(ВÇС)=(АÈВ)Ç(АÈС)	6) Поглощение a) А È (А Ç В) = А b) А Ç (А È В) = А
7) Дополнение к U и Æ a) = Æ b) = U	8) Законы де Моргана a) = Ç b) = È
9) Двойное дополнение:	10) Признаки пустого множества и универсала a) Если "А, АÈВ=А, то В=Æ; b) Если "А, АÇВ = А, то В=U.
11) Признак дополнения Если АÈВ=U и АÇВ=Æ, то (или )	12) Выражение для разности .

 

P(A) - булеан множества А (множество всех подмножеств множества А). Его мощность равна | P (A)| = 2^{| A |} .

 

Прямым (декартовым) произведением множеств X и Y (X´Y) называется совокупность всех упорядоченных пар < x, y >, где x ÎX, y ÎY.

 

Бинарное отношение - подмножество прямого произведения двух множеств: r Í X´Y.

 

 

Пример 1. Покажите на диаграмме Венна выполнение закона дистрибутивности объединения относительно пересечения.

 

Решение: По условию задачи требуется продемонстрировать на диаграмме Венна справедливость равенства: А È(В Ç С)=(А È В)Ç(А È С). Изобразим на диаграммах Венна по отдельности левую и правую части этого равенства. Левая часть – это объединение множеств А (прямоугольники 1,2,5,6) и В Ç С (прямоугольники 1 и 3). Искомому множеству соответствует область, заштрихованная хотя бы один раз, т.е. набор прямоугольников 1,2,3,5,6 (рис. 1). Правая часть – это пересечение множеств А È В (прямоугольники 1-6) и А È С (прямоугольники 1-3 и 5-7). Искомому множеству соответствует область, заштрихованная дважды, т.е. набор прямоугольников 1,2,3,5,6 (рис. 2). Итак, каждому из множеств А È(В Ç С) и (А È В)Ç(А È С) соответствует один и тот же набор прямоугольников. Следовательно, выполнение закона дистрибутивности объединения относительно пересечения подтверждено изображением на диаграмме Венна.

 

Замечание. Для решения данной задачи, в принципе, не обязательно штриховать соответствующие области, а достаточно лишь выписать номера прямоугольников для множеств левой и правой частей равенства:

А ={1,2,5,6}, В Ç С ={1, 3}, А È(В Ç С)={1,2,3,5,6};

А È В ={1-6}, А È С ={1-3, 5-7}, (А È В)Ç(А È С)={1,2,3,5,6}.

 

Пример 2:

Упростить выражение.

 

Пример 3.

Рассчитать мощность множества.

Пример 4.

Рассчитать Булеан.

 

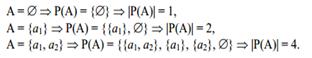
Пример 5.

Произведение множеств.

У П Р А Ж Н Е Н И Я

1. Даны 2 множества: A =(1; 3), B =(2; 4).
Составьте множества А È В, А Ç В, А \ В, А Ä В.

2. Даны конечные множества: A ={ a, b, c, h, z }, B ={ a, c, e, f, z }, C ={ a, d, e, h }.

Из каких элементов состоят множества А\В, ВÄС, (AÄB) ÇC?

3. Изобразите на диаграмме Венна-Эйлера следующие множества:
а) ; б) ; в) ;

г) ; д) ; e)

4. Даны множества A, B, C. При помощи операций È, Ç, \ запишите
множество элементов, которые принадлежат:

а) всем трём указанным множествам;

б) по крайней мере, одному из этих множеств;

в) любым двум из этих множеств, но не принадлежат всем трём;

г) по крайней мере, двум из этих множеств;

д) любому одному из этих множеств, но не принадлежат двум другим.

5. Какие отношения включения справедливы для следующих пар
множеств:

a) и ;

б) и ;

в) и ;

г) и .

6. Покажите на диаграмме Венна-Эйлера выполнение законов де Моргана
и закона ассоциативности для симметрической разности.

7. Проверьте на диаграмме Венна, выполняются ли законы:
а) ассоциативности разности;

б) дистрибутивности объединения относительно симметрической
разности;

в) дистрибутивности пересечения относительно симметрической
разности.

8. Даны множества:
, ,

.
Изобразите на плоскости (x, y) множества
; ; ; .

9. С помощью диаграммы Венна-Эйлера упростите выражения:

а) ; б) ; в) ;

г) ; д) ;

е) .

10. Замените знак * операцией алгебры множеств (È, Ç, \, Ä) так, чтобы
равенство было верным:

а) ;

б) .

Ответ обоснуйте с помощью диаграммы Венна.

11. Какому множеству соответствуют прямоугольники диаграммы Венна
для трёх множеств со следующими номерами:

а) 2, 3, 7; б) 6, 7; в) 4, 5?

Запишите это множество с помощью не более чем трёх операций алгебры множеств: È, Ç, \, Ä (каждая операция считается столько раз, сколько встречается в этом выражении; абсолютное дополнение можно использовать сколько угодно раз). Изобразите полученный результат на диаграмме Венна.

12. Докажите утверждение: .

13. Упростите выражения с помощью законов алгебры множеств:

a) ; б) ;

в) ;

г) ;

д) ;

е) ;

ж) ;

з) ;

и) .

14. Составьте множество всех подмножеств (булеан) множества А, если

а) , б) ,

в) .

15. Даны 2 множества: A ={2; 3}, B ={5; 6}.
а) Составьте множества , , .

б) Какова мощность множества ?
Выпишите любые 4 элемента этого множества.

в) Из каких элементов состоит заданное на множестве бинарное
отношение ?

16. Даны 2 множества: A ={1; 2; 3}, B ={4; 5; 6}.
а) Составьте множества и .

б) Какова мощность множеств 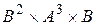и ?
Выпишите любые 4 элемента каждого из этих множеств.

в) Из каких элементов состоит заданное на множестве бинарное
отношение ?

17. Даны множества: A=[0; 3], B=[-1; 1].

Изобразите на плоскости (x; y) прямое произведение этих множеств
и .

18. Проверьте справедливость четырех законов дистрибутивности (´ относительно È; ´ относительно Ç; È относительно ´; Ç относительно ´) на примере множеств A =[0; 1], B =[1; 2], C =[-1; 3]. Изобразите в пространстве (x; y; z) множества , , .

 

Практическое занятие

по «Дискретной математике»
Тема: Основы комбинаторики

Комбинаторикой называется область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из элементов заданного множества. Составляя комбинации, мы фактически выбираем из этого множества различные элементы и объединяем их в группы по нашим потребностям, поэтому вместо слова "комбинации", часто используют слово "выборки" элементов.

Перестановками называются такие выборки элементов, которые отличаются только порядком расположения элементов, но не самими элементами, количество элементов не меняется.

Например необходимо узнать сколькими способами можно расположить 5 книг на полке, для этого следует воспользоваться формулой перестановок.

Если перестановки производятся на множестве n элементов, их число определяется по формуле P_n = n!

Таким образом, если на полке имеется 5 книг, нам необходимо вычислить сколькими способами возможно их расставить, общее число перестановок 5-ти книг P₅ = 5! = 1·2·3·4·5 = 120.

Пример 1.

На книжной полке стояло 30 томов. Ребенок уронил книги с полки, а затем расставил их в случайном порядке. Какова вероятность того, что он не поставил 1-й и 2-й тома рядом?

Решение. Сначала определим вероятность события А, состоящего в том, что ребенок поставил 1-й и 2-й тома рядом.

Элементарное событие - некая расстановка книг на полке. Понятно, что общее число всех элементарных событий будет равно общему числу всех возможных перестановок P30=30!.

Число элементарных событий, благоприятствующих событию А, равно числу перестановок, в которых 1-й и 2-й тома стоят рядом. Мы рассматривали такие перестановки, решая предыдущую задачу, и получили 2·29! перестановок.

Вероятность определяем делением числа благоприятствующих элементарных событий на число всех возможных элементарных событий:

P(A) = 2·29!/30! = 2·29!/(29!·30) = 2/30 = 1/15.

Событие В - ребенок не поставил 1-й и 2-й тома рядом - противоположно событию A, значит его вероятность P(B) = 1 − P(A) = 1−1/15 = 14/15 = 0,9333

Ответ: 0,9333.

 

Размещения.

Размещениями из n элементов по m (мест) называются такие выборки, которые имея по m элементов, выбранных из числа данных n элементов, отличаются одна от другой либо составом элементов, либо порядком их расположения.

Например имеется полка с книгами. Надо узнать сколькими способами можно вынимать по m книг из имеющихся n книг. Здесь важен порядок элементов. То есть комьинация (1,2) не равна комбинации (2,1). Если 1,2,3,4,5 – номера книг.

Число размещений из n по m обозначается A^m_n и определяется по формуле

A_n^m = n·(n − 1)·(n − 2)·...·(n − m + 1) =

 

Попробуем вычислить по этой формуле A_nⁿ, т.е. число размещений из n по n.
A_nⁿ = n ·(n -1)·(n -2)·...·(n - n +1)= n ·(n -1)·(n -2)·...·1= n!
Таким образом, A_nⁿ = P_n = n!

 

Пример 2.

Сколькими способами можно расставить 15 томов на книжной полке, если выбирать их из имеющихся в наличии 30-ти книг?

Решение.Определим общее число размещений из 30 элементов по 15 по формуле

A¹⁵₃₀= = =30*29*28*27*…..*16=202843204931727360000

Ответ: 202843204931727360000.

 

Пример 3.

Сколькими способами можно расставить 30 книг на двух полках, если на каждой из них помещается только по 15 томов?

Решение.Способ I.

Представим себе, что первую полку мы заполняем так же, как в предыдущей задаче. Тогда вариантов размещения из 30-ти книг по 15 будет A3015 = 30·29·28·...·(30−15+1) = 30·29·28·...·16.

И при каждом размещении книг на первой полке мы еще P₁₅ = 15! способами можем расставить книги на второй полке. Ведь для второй полки у нас осталось 15 книг на 15 мест, т.е. возможны только перестановки.

Всего способов будет A₃₀¹⁵·P₁₅, при этом произведение всех чисел от 30 до 16 еще нужно будет умножить на произведение всех чисел от 1 до 15, получится произведение всех натуральных чисел от 1 до 30, т.е. 30!

 

Пример 4.

На книжной полке находится собрание сочинений одного автора в 6 томах. Книги одинакового формата расположены в произвольном порядке. Читатель, не глядя, берет 3 книги. Какова вероятность того, что он взял первые три тома?

Решение.Событие A - у читателя первые три тома. С учетом порядка выбора он мог взять их 6-ю способами. (Это перестановки из 3-ёх элементов P₃ = 3! = 1·2·3 = 6, которые легко перечислить 123, 132, 213, 231, 312, 321.)

Таким образом, число благоприятствующих элементарных событий равняется 6.

Общее число возможных элементарных событий равно числу размещений из 6-ти по 3, т.е. A₆³ = 6·...·(6−3+1) = 6·5·4 = 120.

P(A) = 6/120 = 1/20 = 0,05.

Ответ: 0,05.

 

Сочетания.

 

Сочетания - это те же самые размещения,только в этом случает порядок элементов не учитывается. То есть (1,2,3) и (1,3,2) – это одно и то же.

Неупорядоченные выборки называются сочетаниями из n элементов по m и обозначаются С_n^m.

Число сочетаний определяется по формуле

С_n^m =

Пример 5.

Сколькими способами можно расставить 15 томов на книжной полке, если выбирать их из имеющихся в наличии внешне неразличимых 30-ти книг?

Решение.Мы решаем эту задачу в контексте работы дизайнера интерьеров, поэтому порядок следования на полке 15-ти выбранных внешне одинаковых книг не имеет значения. Нужно определить общее число сочетаний из 30 элементов по 15 по формуле

С₃₀¹⁵ = 155117520.

Ответ: 155117520.

Пример 6.

Сколькими способами можно расставить 30 внешне неразличимых книг на двух полках, если на каждой из них помещается только по 15 томов?

Порядок следования книг на каждой из полок несущественен.

Решаем аналогично примеру 3, заменяя формулу размещения формулой сочетания.

В этом случае ответ будет такой же, как в предыдущей задаче - 155117520 способов, потому что первую полку заполняем выборками-сочетаниями из 30 по 15, а на вторую помещаем остальные 15 книг без учёта перестановок. Поэтому комбинации на второй полке не учитываются (нам надо расставить оставшиеся 15 книг на полку вмещающую 15 книг без учета порядка – всего 1 вариант расстановки).

Пример 7.

На книжной полке находится собрание сочинений одного автора в 6 томах. Книги одинаково оформлены и расположены в произвольном порядке. Читатель берет наугад 3 книги. Какова вероятность того, что он взял первые три тома?

Решение.Событие A - у читателя первые три тома. Это 1-й, 2-й и 3-й тома. Без учета порядка, в котором он выбирал книги, а только по конечному результату, он мог взять их одним способом. Число благоприятствующих элементарных событий - 1.

Общее число возможных элементарных событий равно числу групп из 6-ти по 3, образованных без учета порядка следования элементов в группе, т.е. равно числу сочетаний С63 = 6!/3!/(6 - 3)! = 4·5·6/(1·2·3) = 4·5 = 20.

P(A) = 1/20 = 0,05. Ответ: 0,05.

ЗАДАЧИ И УПРАЖНЕНИЯ

1. Из города А в город В ведут пять дорог, а из города В в город С — три дороги. Сколько путей, проходящих через В, ведут из А в С?

2. Из двух спортивных обществ, насчитывающих по 100 фехто­вальщиков каждое, надо выделить по одному фехтовальщику для участия в состязании. Сколькими способами может быть сделан этот выбор?

3. Имеется пять видов конвертов без марок и четыре вида ма­рок одного достоинства. Сколькими способами можно выбрать кон­верт с маркой для посылки письма?

4. Сколькими способами можно выбрать гласную и согласную буквы из слова «камзол»?

5. То же самое из слова «здание»?

6. Бросают игральную кость с шестью гранями и запускают волчок, имеющий восемь граней. Сколькими различными способами могут они упасть?

7. На вершину горы ведут пять дорог. Сколькими способами турист может подняться на гору и спуститься с нее? То же самое при условии, что спуск и подъем происходят по разным путям.
8. На ферме есть 20 овец и 24 свиньи. Сколькими способами можно выбрать одну овцу и одну свинью? Если такой выбор уже сделан, сколькими способами можно сделать его еще раз?
9. Сколькими способами можно указать на шахматной доске два квадрата—белый и черный? А если нет ограничений на цвет выбранных квадратов?

10. Сколькими способами можно выбрать на шахматной доске белый и черный квадраты, не лежащие на одной и тон же горизон­тали и вертикали?

 

11. Из 12 слов мужского рода, 9 женского и 10 среднего надо выбрать по одному слову каждого рода. Сколькими способами мо­жет быть сделан этот выбор?

12. Имеется 6 пар перчаток различных размеров. Сколькими способами можно выбрать из них одну перчатку на левую руку и одну—на правую руку так, чтобы эти перчатки были различных размеров?
13. Из 3 экземпляров учебника алгебры, 7 экземпляров учеб­ника геометрии и 7 экземпляров учебника тригонометрии надо вы­брать по одному экземпляру каждого учебника. Сколькими спосо­бами это можно сделать?

14. В букинистическом магазине лежат 6 экземпляров романа И. С. Тургенева «Рудин», 3 экземпляра его же романа «Дворянское гнездо» и 4 экземпляра романа «Отцы и дети». Кроме того, есть 5 томов, содержащих романы «Рудин» и «Дворянское гнездо», и 7 томов, содержащих романы «Дворянское гнездо» и «Отцы и дети». Сколькими способами можно сделать покупку, содержащую по од­ному экземпляру каждого из этих романов?
15. Та же задача, если, кроме того, в магазине есть 3 тома, в которые входят «Рудин» и «Отцы и дети».
16. В корзине лежат 12 яблок и 10 апельсинов. Ваня выбирает из нее яблоко или апельсин, после чего Надя берет и яблоко, и апельсин. В каком случае Надя имеет большую свободу выбора: если Ваня взял яблоко или если он взял апельсин?
17. Имеются три волчка с 6, 8 и 10 гранями соответственно. Сколькими различными способами могут они упасть? Та же задача, если известно, что по крайней мере два волчка упали на сторону, помеченную цифрой 1.

18. Сколькими способами можно выбрать три различные краски из имеющихся пяти?

19. Сколькими способами можно составить трехцветный полосатый флаг, если имеется материал 5 различных цветов? Та же за­дача, если одна из полос должна быть красной?

20. Сколько словарей надо издать, чтобы можно было непо­средственно выполнять переводы с любого из пяти языков: русского, английского, французского, немецкого, итальянского, на любой дру­гой из этих пяти языков?

21. На сколько больше словарей придется издать, если число различных языков равно 10?

22. Сколькими способами можно выбрать из полной колоды карт но одной карте каждой масти? То же самое при условии, что среди вынутых карт нет ни одной пары одинаковых, то есть двух коро­лей, двух десяток и т. д.

23. Сколькими способами можно выбрать из полной колоды карт (содержащей 52 карты) по одной карте каждой масти так, чтобы карты красных мастей и карты черных мастей образовывали пары (например, девятки пик и треф и валеты бубен и червей)?
24. У англичан принято давать детям несколько имен. Сколь­кими способами можно назвать ребенка, если общее число имен равно 300, а ему дают не более трех имен?

25. Несколько человек садятся за круглый стол. Будем считать, что два способа рассадки совпадают, если каждый человек имеет одних и тех же соседей в обоих случаях. Сколькими различными способами можно посадить четырех человек? А семь человек? Во скольких случаях два данных человека из семи оказываются со­седями? Во скольких случаях данный человек (из семи) имеет двух данных соседей?

26. Пять девушек и трое юношей играют в городки. Сколькими способами они могут разбиться на две команды по 4 человека в ка­ждой команде, если и каждой команде должно быть хотя бы по одному юноше?

27. Надо послать 6 срочных писем. Сколькими способами это можно сделать, если для передачи писем можно послать трех курье­ров и каждое письмо можно дать любому из курьеров?
28. У одного человека есть 7 книг по математике, а у другого— 9 книг. Сколькими способами они могут обменять книгу одного на книгу другого?