Ниже излагается метод, позволяющий уточнить формулу (11). Этот метод, уточняющий стандартную теорию возмущений, заимствован из теории рассеяния частиц Бозе–Эйнштейна [3]. Ниже предлагается модификация этого метода применительно к частицам Ферми –Дирака.
Если в начальном состоянии исследуемая система обладала одним нейтроном и одним рассеиваемом на нем электроном, находящимся в состоянии с импульсом 
, то волновая функция системыимела вид 
.. Если же в начальном состоянии электрон отсутствовал, то 
. Суперпозиция волновых функций 
вновь является волновой функцией системы, но с неопределенным числом электронов. Такой вид начального состояния системы является возможным, и для дальнейшего будет иметь принципиальное значение. Предварительно пронормируем волновую функцию 
на единицу. Так как
,
То искомая волновая функция имеет вид
. (13)
“ Среднее ” число частиц в системе при этом равно
.
Волновая функция (13) построена по аналогии с волновой функцией когерентного состояния фотонного поля [4], и обладает похожими математическими свойствами. В частности, в этом состоянии квантовое среднее оператора 
отлично от нуля
,
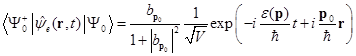Нас будет интересовать конструкция 
, где усреднение проводится по состоянию системы после процесса рассеяния. “ Среднее ” число частиц в состоянии с импульсом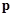 
, если в начальный момент времени частица обладала импульсом , определяет собой вследствие рассеяния вероятность 
перехода электрона из начального состояния в конечное.
Аналогично представлению (4), согласно определению имеем
,
где
,
,
.
Будем говорить о когерентном канале рассеяния, при котором в результате рассеяния нейтрон остается в прежнем состоянии. В результате некогерентного рассеяния нейтрон заменяется протоном.
Пусть согласно определению
, 
, (14)
, 
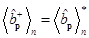. (15)
Воспользовавшись очевидным неравенством
,
находим, что
. (16)
Аналогично
. (17)
Таким образом
.
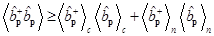Это, не связанное с теорией возмущений, неравенство дает возможность оценить снизу сечение рассеяния. В низшем порядке теории возмущений из (14) и (10) следует
(18)
Аналогично, из (15) посредством (6) имеем
. (19)
Сечение рассеяния
«Среднее» число частиц в начальном состоянии, описываемом волновой функцией (13), равно
.
Среднее число частиц в состоянии с импульсом 
после рассеяния определяется конструкцией 
. Вероятность перехода одной частицы из начального состояния в конечное при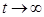 
, таким образом, равно
.
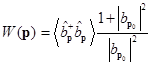Формулы (16-19) показывают, что
,
. (20)
Согласно правилам квантовой теории полная вероятность перехода в единицу времени 
в низшем порядке теории возмущений равна
. (21)
Первое слагаемое этой формулы повторяет результат (11) стандартной теории рассеяния. Второе слагаемое указывает на то, что в резонансной области 
согласно некогерентному каналу рассеяния дополнительно появляется сингулярное слагаемое, существенно увеличивающее сечение процесса рассеяния.
Такой рост вероятности рассеяния наглядно проявляет себя при учете энергетических ширин энергетических уровней рассеивателя, учитываемый параметром 
. Такой учет деформирует формулу (21) следующим образом
.
Теперь ясно видно, что в случае точного резонанса вероятность рассеяния в некогерентном канале вчетверо превосходит вероятность когерентного рассеяния электрона
.
Таким образом, учет некогерентного канала рассеяния полное сечение рассеяния увеличивает в пять раз
. (22)
Вероятность рассеяния электрона в единицу времени 
определяет дифференциальное сечение рассеяния 
согласно следующей формуле
.
Поскольку 
, то нормировочный объем 
из результата выпадает. Согласно (22) учет некогерентного канала рассеяния увеличивает в условиях резонанса сечение рассеяния в пять раз.