Определение 2.1. Окрестностью точки х 0 называется любой интервал (a,b), содержащий эту точку.
e -окрестностью точки х 0 называется интервал (х 0–e; х 0 +e)
 |
|
Поэтому в дальнейшем, говоря об окрестности точки, будем, чаще всего, подразумевать ее e-окрестность. Будем обозначать окрестность точки х 0 символом 
или U(x 0).
Определение 2.2. Точка х 0 называется предельной точкой множества D, если в любой ее окрестности содержится бесконечное число точек множества D.
Например, для множества D = [–1;3)È(3;5] точки х = 3, х = 2, х = 5 – предельные, а вот точка х = 6 предельной не является.
Определение 2.3. Пусть х 0 – предельная точка множества D и у = f (x) функция, определенная на множества D. Число А называется пределом функции 
в точке х 0 (при х, стремящемся к х 0), если для любой окрестности U(A) точки А существует окрестность U(x 0) точки х 0 такая, что для всех х Î U(x 0) выполняется условие f (x) Î U(A). Обозначается
.
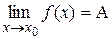Если воспользоваться определением e-окрестности, то определение 2.3 можно сформулировать «на языке e-d»
Определение 2.4. Число А называется пределом функции у = f (x) в точке х 0, если " e > 0 $ d > 0 такое, что " х: | x – x 0| < d Þ | f (x) – A|<e.
Определение 2.5. Число А называется пределом функции у = f (x) при х стремящемся к бесконечности, если " e > 0 $ N > 0 такое, что " х: | x |> N выполняется | f (x) – A| < e. Обозначается 
.
В частности, если f = f (n) – функции натурального аргумента, определяющая последовательность ап, то из определения 2.5 получим определение предела последовательности:
Определение 2.6 Число А называется пределом последовательности { ап }, если " e > 0 $ такой номер N, что начиная с этого номера все члены последовательности удовлетворяют условию | ап – A| < e. Обозначается 
.
В этом случае говорят, что последовательность { ап } сходится к числу А.
В приведенных определениях число А подразумевается конечным. Если же А = ¥, то в этом случае говорят, что функция f (x) стремится к бесконечности и называют ее бесконечно большой в соответствующей точке. Таким образом
Определение 2.7. Функция f (x) называется бесконечно большой в точке х 0, если " М > 0 $ d > 0 такое, что " х: | x – x 0| < d Þ | f (x)| > M.
Задание: Самостоятельно сформулировать определение бесконечно большой функции при х ® ¥, х ® +¥, х ® – ¥.
2. Односторонние пределы. Критерий существования предела функции в точке.
Из определений 2.1-2.7 следует что:
1) f (x) не обязательно определена в точке х 0.
2) величина d (или N в определениях 2.5. и 2.6), вообще говоря, зависит от e, т.е. d = d(e).
Кроме того, не регламентируется характер приближения х к х 0, т.е. принимая значения, сколь угодно близкие к х 0, х может быть как больше х 0, так и меньше х 0. Рассмотрим пример.
Функция 
определена на всей числовой прямой, точка х 0 = 1 – предельная точка области определения этой функции. Найдем предел этой функции в точке х 0 = 1. Рассмотрим график этой функции (рис.5). Стрелка на графике означает, что точка (1, 2) не лежит на соответствующей части графика функции.
По графику видно, что «претендентами на звание»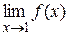 
являются числа А1 = 2 и А2 = 1. Но согласно определению предела, ни одно из этих чисел не является пределом данной функции в рассмотренной точке. Действительно, какую бы окрестность точки А1 = 2 мы не взяли, невозможно указать окрестность точки х 0 = 1, для всех значений х из которой значения функции попали бы в окрестность точки А1 (рис.6а):
f (x 1) ÏU(A1), f (x 2) Î U(A1).
То же касается и точки А2(рис.6б), на сей раз f (x 1) ÎU(A2), а f (x 2) Ï U(A2).
 |
Но если наложить ограничения на характер изменения переменной х, например, потребовать, чтобы х ® 1, но при этом оставалось меньше 1, то 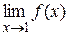= 2. Если же при х ® 1 потребовать х > 1, то 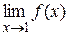= 1. Такие пределы называются односторонними.
Определение 2.8. Число А называется правосторонним пределом (пределом справа) функции у = f (x) в точке х 0, если " e > 0 $ d > 0 такое, что " х, x – x 0 < d Þ | f (x) – A| < e. Обозначается
.
Таким образом, правосторонний предел равен
Определение 2.9 Число А называется левосторонним пределом (пределом слева) функции у = f (x) в точке х 0, если " e > 0 $ d > 0 такое, что " х, x 0 – x < d Þ | f (x) – A| < e. Обозначается 
.
Итак, предел слева равен 
.
Справедлива следующая
Теорема 2.1. (Критерий существования предела)
Для того, чтобы функция f (x) в точке х 0 имела конечный предел, необходимо и достаточно, чтобы существовали конечные односторонние пределы f (x 0+0) и f (x 0–0) и эти пределы были равны между собой:
f (x 0+0) = f (x 0–0).
3. Бесконечно малые и бесконечно большие функции.
Если же f (x 0+0) или f (x 0–0), или оба эти предела бесконечны, то как мы уже говорили, функция является бесконечно большой (справа или слева) в точке х 0.
Например, для функций, график которой изображен на рис.7а, имеем f (x 0+0) = f (x 0 –0) = +¥, значит функция бесконечно большая в точке х 0; для функции, график которой представлен на рис.7б, f (x 0+0) = +¥, f (x 0–0) = –¥; функция с графиком 7в) имеет f (x 0–0) = 1, f (x 0+0) = +¥, значит функция бесконечно большая справа в точке х 0.
Заметим также, что на графике 7в) f (х) ® + ¥ при х ® + ¥ и при х ® – ¥, тогда как на графике 7а) f (х) ® 0 при х ® ± ¥.
Определение 2.10. Функция у = a(х) называется бесконечно малой в точке х 0 (или при х ® х 0), если " e >0 $ d > 0 такое, что " х, | x – x 0| < d выполняется неравенство |a(x)|< e.
Таким образом, бесконечно малая в точке х 0 функция – это функция, предел которой в этой точке равен нулю.
Например, функция 
бесконечно малая в точке х =3, а функция 
бесконечно малая при х ® ± ¥.
Теорема 2.2. (свойства бесконечно малых)
Если a(х) и b(х) – бесконечно малые в точке х 0, и (х) – ограниченная в окрестности этой точки функция, а с – произвольная константа, то функции a(х) + b(х), a(х) – b(х), a(х).b(х), с. a(х), и (х).a(х) есть также бесконечно малые в точке х 0 функции, а 
– бесконечно большая в точке х 0 функция.
Доказательство: Если a(х) и b(х) – бесконечно малые в точке х 0, то "e>0
$ d1>0 такое, что " х, | x – x 0| < d1 выполняется неравенство |a(x)|< 
,
и $ d2>0 такое, что " х, | x – x 0| < d2 выполняется неравенство |b(x)|< 
.
Тогда, если взять d = min(d1,d2), то "e>0 из неравенства | x – x 0| < d будет следовать неравенство
| a(х) ± b(х)| < |a(x)| +|b(x)|< + = e,
а это и означает, что функции a(х) + b(х) и a(х) – b(х) – бесконечно малые в точке х 0.
Остальные свойства докажите самостоятельно или разберите доказательства, предложенные в учебниках:
1. Пискунов Н.С. Дифференциальное и интегральное исчисление. Том 1.
2. Шипачёв В.Н. Высшая математика.
Заметим, что в теореме 2.2 ничего не сказано об отношении двух бесконечно малых функций, поскольку в результате может быть получена как бесконечно малая функция, так и функция, имеющая не равный нулю предел, так и бесконечно большая функция. Поэтому отношение двух бесконечно малых функций принято называть неопределенностью и обозначать 
.
Теорема 2.3(Свойства бесконечно больших)
Если функции f (x) и g (x) – бесконечно большие в точке х 0, и (х) – ограниченная в окрестности этой точки функция, а с – произвольная константа, то функции f (x). g (x), сf (x), и (х). f (x) – бесконечно большие в точке х 0 функции, а 
– бесконечно малая в этой точке функция.
Доказательство этого утверждения так же можно посмотреть в перечисленных выше учебниках.
Если функции f (x) и g (x)бесконечно большие, то относительно функций f (x) ± g (x) нельзя однозначно сказать, какими они являются. Все зависит от скорости роста этих функций, и их знака. Например, сумма положительных бесконечно больших, или сумма отрицательных бесконечно больших функций есть бесконечно большая (того же знака) функция, а разность бесконечно больших положительных функций может оказаться и бесконечно большой, и бесконечно малой, и имеющей конечный предел в данной точке функцией. Аналогичное замечание можно сделать и относительно функции 
. Поэтому алгебраическую сумму функций f (x) ± g (x) и частное бесконечно больших функций называют неопределенностью и обозначают 
и 
соответственно.
4. Теоремы о пределах
Теорема 2.4.
Число А является пределом функции f (х) в точке х 0 тогда и только тогда, когда в окрестности точки х 0 функция представима в виде
f (x) = А + a(х),
где a(х) – бесконечно малая в точке х 0 функция.
Доказательство:
1) (необходимость) Пусть 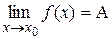. Значит, "e >0 $ d >0 такое, что " х, таких что | x – x 0| < d, выполняется неравенство | f (x) – A| < e. Обозначим разность f (x) – A = a(х). Тогда " e > 0 $ d > 0 такое, что " х, | x – x 0| < dвыполняется условие | a(х)| < e, следовательно, функция a(х) – бесконечно малая в точке х 0.
2)(достаточность) Пусть в окрестности точки х 0 имеет место f (x) = А + a(х), где a(х) бесконечно малая. Тогда для a(х) = f (x) – A имеем: " e > 0 $ d > 0 такое, что " х, | x – x 0| < d Þ | a(х)| = | f (x) – A| < e. Последнее, по определению предела, означает, что 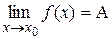. ЧТД.
Теорема 2.5.(Свойства пределов)
Пусть существуют конечные пределы ,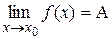 
, и С – произвольная константа. Тогда:
1) 
;
2) 
;
3) 
;
4) 
;
5) 
, если В ¹ 0;
Доказательство:
1) Пусть у (х) = С – постоянная функция. Тогда, по определению предела, " e > 0 $ d > 0 такое, что " х, | x – x 0| < d Þ | у (х) – С | = | С – С | < e, значит, . ЧТД.
2) Пусть у (х) = С.f (x). Так как 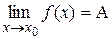, то f (x) = A + a(x), где a(x) бесконечно малая (теорема 2.4). Умножив обе части этого равенства на С, получим
С.f (x) = С A + С. a(x),
но С. a(x) – бесконечно малая (см. теорему 2.2). Значит, функция С.f (x) представлена в виде суммы числа С А и бесконечно малой С. a(x), следовательно (по теореме 2.4), число С А есть предел этой функции, т.е.
. ЧТД.
3) Так как 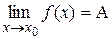, , то f (x) =A+a1(x), g (x) = B +a2(x), где a1(x), a2(x) – бесконечно малые. Тогда
f (x) ± g (x) = (A + a1(x)) ± (B + a2(x)) = (А ± В) + (a1(x) ± a2(x)).
А так как a1(x) ± a2(x) – бесконечно малые, то по теореме 2.4, числа (А ± В) есть пределы функций f (x) ± g (x) соответственно. ЧТД.
4) Аналогично, если 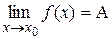, , то
f (x) = A + a1(x), g (x) = B + a2(x),
где a1(x), a2(x) – бесконечно малые. Тогда
f (x) .g (x) = (A + a1(x)). (B + a2(x)) = А. В + А. a2(x) + В. a1(x)+ a1(x). a2(x),
но, по теореме 2.2, А. a2(x), В. a1(x), a1(x). a2(x) – бесконечно малые, значит, функция f (x) .g (x) представлена в виде суммы числа АВ и бесконечно малой, значит число АВ есть предел данной функции в точке х 0. Таким образом
, ЧТД.
Остальные свойства докажите самостоятельно или разберите доказательства по указанным выше учебникам.
Перечисленные свойства позволяют вычисление пределов функций свести к вычислению значений функции в предельной точке. Действительно, пользуясь свойствами, получим, например,
Легко убедиться в том, что значение данной функции в точке х =1 также равно 8.
Рассмотрим также пример применения свойств бесконечно малых и бесконечно больших функций:
= 
.
Здесь вычисление предела начали с преобразования функции – каждое слагаемое числителя разделили на знаменатель. Заметим, что непосредственная подстановка предельного значения переменной х привела бы к выражению вида 
, которое называется неопределенностью. Неопределенности различного вида, возникающие при вычислении предела, устраняются (говорят: раскрываются) в результате преобразования функции. Рассмотрим еще один пример, в котором раскрывается неопределенность вида :
.
Вычисление предела функции можно проводить по следующей схеме
В практических занятиях будут даны некоторые рекомендации по раскрытию упомянутых неопределенностей.
Рассмотрим без доказательства теоремы, позволяющие осуществлять предельный переход в неравенствах.
Теорема 2.6
Если существуют конечные пределы 
, 
и f (x) £ g(x) в окрестности точки х 0, то £ .
Теорема 2.7.
Если в окрестности точки х 0 выполняется условие f (x) £ j (х) £ g (x) и существуют = А и = А, то существует 
= А.
Теорема 2.8.
Если функция f (x) имеет конечный предел в точке х 0, то она ограничена в некоторой окрестности этой точки.
В частности, эти теоремы используются для доказательства двух важных в математическом анализе формул, которые носят название замечательных пределов.