Схема исследования функции на экстремум
1. Находим частные производные функции нескольких переменных по всем переменным и приравниваем их к нулю.
2. Определяем стационарные точки функции, т.е. те в которых частные производные по всем переменным равны нулю или хотя бы одна из них не существовала.
3. Используя достаточное условие экстремума делаем заключение о наличии или отсутствии экстремума в критических точках.
Правило определения экстремума двух переменных.
Чтобы определить экстремум  (двух переменных) следует:
(двух переменных) следует:
1. Определить стационарные точки в которых функция может достигать экстремума, для чего решаем систему уравнений
 или
или 
2. Находим вторые частные производные  ,
,  ,
,  или
или  ,
,  ,
,  .
.
3. Вычислить значения вторых частных производных в каждой стационарной точке, а полученные числа обозначить соответственно через  ,
,  ,
, 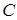 .
.
4. Составляем выражение 
При этом,
а) Если  , то экстремум в стационарной точке есть
, то экстремум в стационарной точке есть
I. Если  (или
(или  ), то будет минимум
), то будет минимум
II. Если  (или
(или  ), то будет максимум
), то будет максимум
б) Если  , то экстремума в рассматриваемой стационарной точке нет
, то экстремума в рассматриваемой стационарной точке нет
в) Если  , то имеет место сомнительный случай и для заключения об экстремуме требуется воспользоваться частными производными порядка выше второго.
, то имеет место сомнительный случай и для заключения об экстремуме требуется воспользоваться частными производными порядка выше второго.
Пример. Исследовать на экстремум  .
. 
Нам известно для функции двух переменных  (1)
(1)
Условие (1) является необходимым условием экстремума.
Достаточные условия экстремума для функции  выражаются с помощью определителя
выражаются с помощью определителя 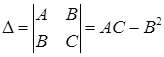 , где
, где  ,
,  ,
, 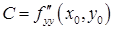 , а именно
, а именно
1. Если  , то
, то  - точка экстремума
- точка экстремума
а) Если  (или
(или  ), то будет минимум
), то будет минимум
б) Если  (или
(или  ), то будет максимум
), то будет максимум
2. Если  , то в точке
, то в точке  экстремума нет
экстремума нет
3. Если  , то требуется дополнительные исследования функции, например, по знаку приращения
, то требуется дополнительные исследования функции, например, по знаку приращения  вблизи этой точки.
вблизи этой точки.
1. Находим частные производные 1го и 2го порядка:





2. Обращаем в ноль все первые производные, получим систему уравнений для определения критических точек.
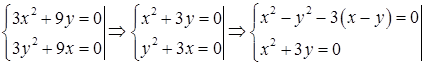
Разбиваем данную систему на две:
А) 
В) 
Решаем систему А)
 .
.  ,
, 
Решаем систему В)

 - комплексные корни. Не принимаем во внимание.
- комплексные корни. Не принимаем во внимание.
Получены две критические точки  и
и  .
.
Вычисляем значения производных второго порядка в этих точках и находим определитель.
 ,
,  ,
, 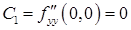
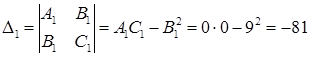
Т.к.  в точке
в точке  нет экстремума (из достаточных условий)
нет экстремума (из достаточных условий)
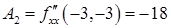 ,
,  ,
, 

Т.к.  и
и  , то в точке
, то в точке  функция имеет максимум, причем
функция имеет максимум, причем

Условный (несвободный) экстремум.
Ранее мы рассматривали локальные экстремумы. Рассмотрим задачу об определении экстремума функции нескольких переменных при наличии дополнительных условий (уравнений связи). Эта задача носит название задачи об условном (относительном) экстремуме.
Пусть на множестве  задана функция
задана функция  ,
,  . На
. На  также определены функции
также определены функции  (
( ).
).
Задача. Найти экстремум  при наличии дополнительных условий (уравнений связи)
при наличии дополнительных условий (уравнений связи)
 (1)
(1)
 Пусть
Пусть  ,
,  .
.
Матрица Якоби

При 
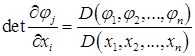 - определитель Якоби (Якобиан).
- определитель Якоби (Якобиан).
Уточним постановку задачи.
Обозначим 
 Пусть
Пусть  ,
,  (
( ) определены на
) определены на  ,
,  ,
,  - множество решений системы (1).
- множество решений системы (1).  называется точкой условного экстремума
называется точкой условного экстремума  при выполнении уравнений (1)
при выполнении уравнений (1) 
 - точка локального экстремума
- точка локального экстремума  на
на  .
.
Замечание. Условный максимум (минимум) – это наибольшее (наименьшее) значение функции в точке  по отношению не ко всем точкам из некоторой окрестности точки
по отношению не ко всем точкам из некоторой окрестности точки  (
( ), а только к тем из них, которые связаны между собой уравнениями связи.
), а только к тем из них, которые связаны между собой уравнениями связи.
Предположим теперь, что
1)  ,
,  ;
; 
2) 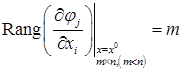
Из условия 2) следует, что один из миноров порядка  матрицы Якоби
матрицы Якоби  .
.
Пусть этот минор 
Тогда согласно теореме о существовании неявных функций в 

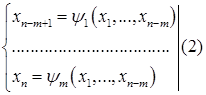
Причем  ,
, 

Рассмотрим сложную функцию


 - точка условного экстремума функции при условии 1)
- точка условного экстремума функции при условии 1) 
 - точка локального экстремума функции
- точка локального экстремума функции  .
.
Доказательство.
Доказательство следует из того, что из теоремы о неявных функциях, условия 1) и 2) – эквиваленты.
 дает метод отыскания условного экстремума, когда уравнения (2) могут быть найдены явно, что не всегда возможно. Отметим далее, что строим матрицу Якоби – координаты градиентов
дает метод отыскания условного экстремума, когда уравнения (2) могут быть найдены явно, что не всегда возможно. Отметим далее, что строим матрицу Якоби – координаты градиентов  , т.е.
, т.е. 
 условие
условие 
 условие независимости строк
условие независимости строк  условие независимости
условие независимости  , т.е. из условия:
, т.е. из условия:

Можно также рассмотреть

 Пусть
Пусть
1) 
2) 
3) 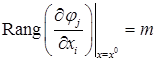
Тогда  - стационарная точка для функции
- стационарная точка для функции 

 .
.
 (3)
(3)
Очевидно (3) условие зависимости 
В скалярном виде оно эквивалентно.
 (4)
(4)
Рассмотрим функцию
 ,
,  (5)
(5)
(5) – функция Лагранжа,  - множитель Лагранжа
- множитель Лагранжа

Условия (4) – эквивалентны условию стационарной функции Лагранжа
 (6)
(6)
Т.е.  , причем
, причем 
Следствие. (Необходимое условие существования условного экстремума)
При указанных условия. Если  - точка условного экстремума, то
- точка условного экстремума, то  - стационарная для функции Лагранжа.
- стационарная для функции Лагранжа.
Доказательство.
 - условный экстремум
- условный экстремум 
 - стационарная точка функции
- стационарная точка функции 

 (3)
(3) 
 , т.е.
, т.е.  ,
,  (6)
(6)
Т.о. для отыскания точек, подозрительных на условный экстремум необходимо найти решение следующей системы:
 (7)
(7)
где  ,
,  . Следовательно
. Следовательно  уравнений относительно
уравнений относительно 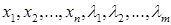 - неизвестных.
- неизвестных.
Замечание 1. Найдем дифференциалы в системе (1)
 (8)
(8)
Для дальнейшего видно, что  дифференциалов
дифференциалов  можно найти из (8), т.к.
можно найти из (8), т.к.  .
.
Замечание 2. Пусть  ,
,
где  (при
(при  ) открытое множество.
) открытое множество.
Пусть множество 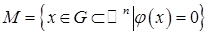 является «
является « » мерным пространством
» мерным пространством  . Рассмотрим отображение
. Рассмотрим отображение 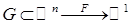 , где
, где
 , причем
, причем  и
и  некоторые постоянные. Тогда для
некоторые постоянные. Тогда для  локального условного экстремума функции
локального условного экстремума функции  на множестве
на множестве  имеем
имеем  при некотором выборе постоянных
при некотором выборе постоянных  . Тем самым задача об отыскании условных экстремумов сводится к решению следующей системы «
. Тем самым задача об отыскании условных экстремумов сводится к решению следующей системы « » уравнений с «
» уравнений с « » неизвестными
» неизвестными 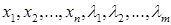

где  ,
,  .
.
Th 3 (Достаточное условие существования условного экстремума)
Пусть
1) 
2) 
3)  - стационарная точка для функции Лагранжа.
- стационарная точка для функции Лагранжа.
Тогда
а) 

 - условный минимум
- условный минимум
б) 

 - условный максимум.
- условный максимум.
Пример 1. Найти условный экстремум функции  при условии
при условии  .
.
Решение.
1й способ.
Составим функцию Лагранжа.

Найдем стационарные (критические) точки, решив систему уравнений:


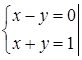




 - критическая точка
- критическая точка





Но 

 . Тогда
. Тогда 
 точка
точка  - точка условного минимума.
- точка условного минимума.
Проверить, что для исходной функции точка  не является минимумом.
не является минимумом.
2й способ. (Возможен не всегда)







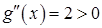 - минимум.
- минимум.
Пример 2. Найти условный экстремум функции  на прямой
на прямой 
Решение.
1) Составим функцию Лагранжа: 
2) 

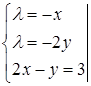


 ,
,  ,
,  . В точке
. В точке 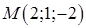
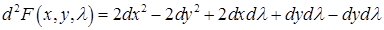 - это есть знакопеременная квадратичная форма. Следовательно, точка
- это есть знакопеременная квадратичная форма. Следовательно, точка 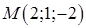 не экстремальная точка функции
не экстремальная точка функции  , но эта точка может быть экстремальной точкой функции
, но эта точка может быть экстремальной точкой функции  при условии связи
при условии связи  . Из этого условия связи имеем
. Из этого условия связи имеем  .учитывая это соотношение для
.учитывая это соотношение для  получаем:
получаем:
 - отрицательно определенная квадратичная форма, и, следовательно, точка
- отрицательно определенная квадратичная форма, и, следовательно, точка  является точкой локального максимума функции
является точкой локального максимума функции  из условия связи
из условия связи  .
.
Пример 3. Исследуем, имеет ли функция  условный экстремум в точке
условный экстремум в точке  , если
, если 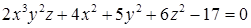 (*).
(*).
Решение.
Составляем функцию Лагранжа 
Координаты 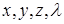 критической точки
критической точки  должны удовлетворять системе:
должны удовлетворять системе:
 (1)
(1)
По проверке убеждаемся, что при  ,
,  ,
,  ,
,  - решение системы (1)
- решение системы (1)
В точке  возможен условный экстремум функции
возможен условный экстремум функции  с условием связи (*), причем
с условием связи (*), причем  .
.
Находим второй дифференциал функции Лагранжа

В силу условий связи
 Поэтому при
Поэтому при  ,
,  ,
,  имеем:
имеем:




 в точке
в точке 

Т.к. в этой точке  является отрицательно определенной квадратичной формой, то функция
является отрицательно определенной квадратичной формой, то функция  в точке
в точке  имеет локальный максимум. Следовательно, точка
имеет локальный максимум. Следовательно, точка  есть точка условного максимума функции
есть точка условного максимума функции  при условии функции связи (*).
при условии функции связи (*).
Пример 4. Найти extr. f. f(x,y,z)= 
Решение. 
 ,
,

Решив систему находим единственную стационарную (.) M (
Определим в этой точке (.) M вторые производные.

 = -1
= -1 

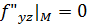
 .
.
Получим матрицу квадратной формы.
А = 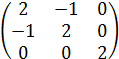
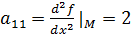




И главные (угловые) миноры.
 >0;
>0;  =
=  =
= 
Т.о матрица порождает положительно определенную квадратичную форму и (.) М Точка min f(x) =  .
.
Пример 5. Исследовать на extr f(x,y)=14  .
.
Решение.
1) 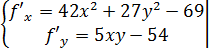

Решив систему,получим 4-ре пары решений, при которых исследуемая функция может иметь extr.

 .
.
2) Определим 2-е производные
 ;
; 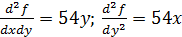
3) Для каждой пары значения определим числа
а) 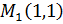 А =
А =  ; B =
; B = 
Число ⩟ =  а так как А= 84 >0,то имеет месть min.
а так как А= 84 >0,то имеет месть min.
Min f(1,1) = 14*1+27*1-69-54=-82.
б)  А =
А =  B =
B = 

⩟ =  =
=  <0 в (.)
<0 в (.)  extr нет.
extr нет.
с)  . А= -84, В = -54, С = -54.
. А= -84, В = -54, С = -54.
⩟ =  = (-84)*(-54)-(-
= (-84)*(-54)-(-  >0 extr есть т.к A=-84 <0 =>max.
>0 extr есть т.к A=-84 <0 =>max.
max f(-1,1)=-14-27+69+54 = 82.
d) 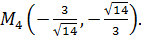 A = -
A = -  C = -
C = -  .
.
⩟ =  =(-
=(-  <0 extr
<0 extr 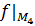 - нет.
- нет.
Пример 6. Исследовать на extr f(x,y,z) = 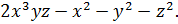
Решение.
 =>
=> 
Решив эту систему, мы получим пять критических точек.
 (
(



 = -2;
= -2;  ;
; 
 ;
;
 .
.
Поставив, преобразовав получим:

Так как  является отрицательно определенной квадратичной формой,то в (.)
является отрицательно определенной квадратичной формой,то в (.)  функция f имеет строгий локальный min.
функция f имеет строгий локальный min.
Для анализа квадратичной формы
 применим Критерий Сильвестра.
применим Критерий Сильвестра.
Матрица этой формы имеет вид:

её главные угловые миноры
2 > 0 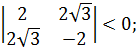
 >0
>0
Распределение знаков этих миноров показывает, что квадратичная форма знакопеременная в (.)  функция не имеет extr. Точка
функция не имеет extr. Точка  – седловая (.) функции.
– седловая (.) функции.
Аналогично в остальных (…)  - (самостоятельно)- убедитесь,что это седловые точки.
- (самостоятельно)- убедитесь,что это седловые точки.