Задание 3. Составить систему уравнений вида  используя данные из таблицы 4 и решить ее с помощью обратной матрицы и методом Крамера.
используя данные из таблицы 4 и решить ее с помощью обратной матрицы и методом Крамера.
Задание 4. Решить систему уравнений методом Гаусса (данные для системы представлены в таблице 5)
Приложение А
Данные для расчетов
Таблица 1 – Данные для матрицы А3´3
| № варианта | а11 | а12 | а13 | а21 | а22 | а23 | а31 | а32 | а33 |
| -1 | |||||||||
| -2 | -1 | ||||||||
| -10 | -2 | ||||||||
| -2 | -1 | ||||||||
| -1 | -1 | -2 | -1 | ||||||
| -1 | -1 | ||||||||
| -5 | |||||||||
| -2 | -1 | ||||||||
| -2 | -1 | ||||||||
| -2 | -1 | ||||||||
| -1 | |||||||||
| -2 | -1 | ||||||||
| -1 | |||||||||
| -2 | -3 | ||||||||
| -2 | -2 | ||||||||
| -1 | -2 | -1 | |||||||
| -1 | -1 | ||||||||
| -1 | -1 | ||||||||
| -1 | -1 | -1 | |||||||
| -3 | -1 | ||||||||
| -2 | |||||||||
| -2 | -2 | -2 | -1 | -1 | |||||
| -1 | -2 | -1 | |||||||
| -1 | |||||||||
| -1 | -2 | ||||||||
| -1 | -2 | ||||||||
| -5 | -1 | ||||||||
| -1 | -1 | -2 | |||||||
| -1 | -2 | -2 |
Таблица 2 – Данные для матрицы В3´3
| № варианта | b11 | b 12 | b 13 | b 21 | b 22 | b 23 | b 31 | b 32 | b 33 |
| -1 | -2 | ||||||||
| -1 | -5 | ||||||||
| -1 | |||||||||
| -1 | -1 | -2 | |||||||
| -2 | -2 | ||||||||
| -3 | -2 | ||||||||
| -1 | -1 | -3 | |||||||
| -2 | -5 | ||||||||
| -7 | -2 | -1 | |||||||
| -3 | -1 | -1 | |||||||
| -1 | |||||||||
| -6 | |||||||||
| -14 | -7 | ||||||||
| -2 | -3 | ||||||||
| -2 | -1 | -1 | |||||||
| -1 | -3 | ||||||||
| -1 | -1 | -3 | |||||||
| -1 | -2 | ||||||||
| -4 | |||||||||
| -1 | -11 | ||||||||
| -1 | -2 | -2 | |||||||
| -1 | |||||||||
| -2 | -3 | -2 | -1 | -3 | |||||
| -1 | |||||||||
| -11 | |||||||||
| -14 | -2 | -2 | |||||||
| -1 | -7 |
Таблица 3 – Данные для матрицы А4´4
| № варианта | а11 | а12 | а13 | а14 | а21 | а22 | а23 | а24 | а31 | а32 | а33 | а34 | а41 | а42 | а43 | а44 |
| -1 | -1 | -2 | ||||||||||||||
| -2 | -3 | -1 | -3 | -5 | -1 | |||||||||||
| -1 | -1 | -1 | -1 | -1 | -1 | |||||||||||
| -2 | -2 | -1 | -1 | -1 | ||||||||||||
| -4 | -1 | -1 | -6 | -1 | ||||||||||||
| -1 | -1 | -1 | -1 | |||||||||||||
| -1 | -3 | -1 | -1 | -1 | -10 | |||||||||||
| -3 | -1 | -1 | ||||||||||||||
| -1 | -1 | -1 | -3 | -1 | ||||||||||||
| -1 | -3 | -1 | -8 | -1 | -1 | |||||||||||
| -1 | -1 | -1 | -2 | |||||||||||||
| -1 | -2 | -1 | ||||||||||||||
| -3 | -6 | -1 | ||||||||||||||
| -2 | -2 | -1 | -1 | -3 | -4 | |||||||||||
| -2 | ||||||||||||||||
| -3 | -1 | -1 | ||||||||||||||
| -1 | -1 | -2 | -6 | -1 | ||||||||||||
| -3 | -4 | -2 | -8 | -1 | -1 | |||||||||||
| -1 | -1 | -2 | ||||||||||||||
| -1 | -2 | -4 | ||||||||||||||
| -4 | ||||||||||||||||
| -1 | -3 |
Таблица 4 – Данные для задания 3
| № варианта | а11 | а12 | а13 | а14 | а21 | а22 | а23 | а24 | а31 | а32 | а33 | а34 | а41 | а42 | а43 | а44 | b1 | b2 | b3 | b4 |
| -3 | -3 | |||||||||||||||||||
| -1 | -1 | -3 | -2 | |||||||||||||||||
| -1 | -5 | -10 | ||||||||||||||||||
| -3 | -2 | -5 | -5 | -5 | -4 | |||||||||||||||
| -3 | -7 | -5 | -1 | -7 | -3 | -1 | -5 | |||||||||||||
| -3 | -1 | -5 | -11 | |||||||||||||||||
| -3 | -2 | -1 | -3 | -6 | ||||||||||||||||
| -1 | -1 | -1 | -2 | -4 | -8 | -3 | ||||||||||||||
| -1 | -1 | -1 | -1 | |||||||||||||||||
| -1 | -1 | -2 | -1 | -1 | -1 | |||||||||||||||
| -1 | -1 | -1 | -5 | -3 | ||||||||||||||||
| -3 | -3 | |||||||||||||||||||
| -3 | -2 | -1 | -1 | |||||||||||||||||
| -4 | -2 | -2 | -8 | -3 | -1 | -1 | -9 |
Таблица 5 – Данные для задания 4
| № варианта | а11 | а12 | а13 | а14 | а21 | а22 | а23 | а24 | а31 | а32 | а33 | а34 | а41 | а42 | а43 | а44 | b1 | b2 | b3 | b4 |
| -3 | -3 | -2 | -1 | -6 | ||||||||||||||||
| -4 | -8 | -3 | -1 | -1 | -1 | -2 | ||||||||||||||
| -2 | -5 | -1 | -2 | -3 | -2 | -1 | -10 | |||||||||||||
| -1 | -1 | -1 | -1 | -2 | -1 | |||||||||||||||
| -3 | -3 | |||||||||||||||||||
| -1 | -1 | -2 | -3 | -2 | -5 | -2 | -10 | |||||||||||||
| -1 | -5 | -10 | ||||||||||||||||||
| -5 | -1 | -3 | -7 | -1 | -5 | -7 | -3 | |||||||||||||
| -2 | -3 | -1 | -1 | |||||||||||||||||
| -5 | -5 | -3 | -2 | -5 | -4 | |||||||||||||||
| -5 | -1 | -3 | -11 | |||||||||||||||||
| -2 | -5 | -1 | -2 | -1 | ||||||||||||||||
| -1 | -1 | -1 | -3 | -5 | ||||||||||||||||
| -2 | -3 | -2 | -4 | -3 | -1 | -7 | -11 |
Приложение Б
Информационный материал практической направленности
| Действия над матрицами: | 1 
|
2 
| |
3 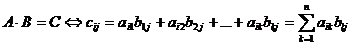
| |
| Вычисление определителя: | 1 
|
2 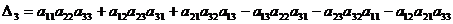
 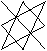 «Правило треугольника»
+ – «Правило треугольника»
+ –
| |
3  , где , где 
| |
| Обратная матрица: |  , где , где 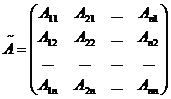 , , 
|
| Матричные уравнения: | 1 
|
2 
| |
| Формулы Крамера: |  , где , где  
 
|
| Метод Гаусса | Прямой ход
С помощью элементарных преобразований расширенная матрица системы  приводится к виду приводится к виду 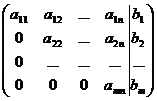 .
Обратный ход
Осуществляется переход к системе и выполняется поиск неизвестных .
Обратный ход
Осуществляется переход к системе и выполняется поиск неизвестных
|
Пример выполнения заданий
Задание 1. Выполнить действия над матрицами  , где
, где  и
и 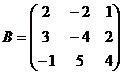 .
.
Решение:
1 Вычислим  :
:
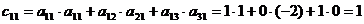


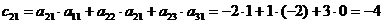
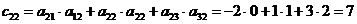




Получили  .
.
2 Вычислим  :
:
 .
.
3 Вычислим 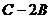 :
:
 .
.
Ответ:  .
.
Задание 2. Вычислить определитель 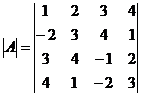 .
.
Решение:
Выполним элементарные преобразования определителя для того, чтобы получить нули для элементов  и
и  .
.
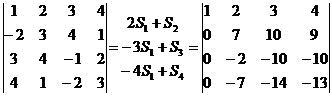 , где Si –соответствующая строка определителя.
, где Si –соответствующая строка определителя.
Запишем разложение по первому столбцу.
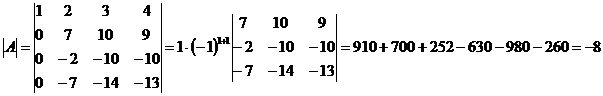 .
.
Определитель третьего порядка вычислен по правилу «Треугольника».
Задание № 3. Решить систему уравнений  методом Крамера и с помощью обратной матрицы.
методом Крамера и с помощью обратной матрицы.
Решение:
1 Метод Крамера
Вычислим определитель матрицы системы:
 .
.
Составим и вычислим дополнительные определители путем замены соответствующего столбца определителя матрицы системы на столбец свободных членов:
 ;
; 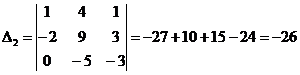 ;
;
 .
.
 ;
;  ;
;  .
.
Ответ:  .
.
2 С помощью обратной матрицы: 
Вычислим обратную матрицу;
 ;
;
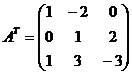 ;
;
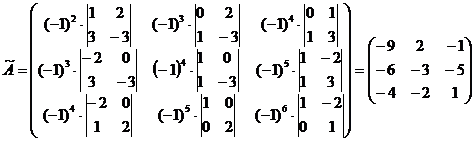 ;
;
 .
.
Вычислим матрицу Х:
 ;
;
 ;
;
 .
.
Ответ:  .
.
Задание 4. Решить систему уравнений  методом Гаусса.
методом Гаусса.
Решение:
Прямой ход
Составим расширенную матрицу системы:
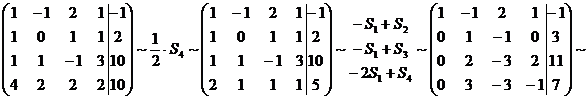
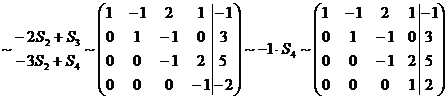 .
.
Si – номер соответствующей строки расширенной матрицы
Обратный ход
Составим систему уравнений:
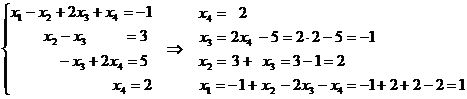
Ответ: 