Д а н о: У равнения движения точки в плоскости xy:
x = –2 cos  + 3; y = 3 sin
+ 3; y = 3 sin  – 1,
– 1,
где x, y – в метрах, t – в секундах.
О п р е д е л и т ь: уравнение траектории точки; найти скорость и ускорение точки для момента времени t = 1 с, а также касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории. Показать векторы скорости и ускорения этой точки.
 Р е ш е н и е
Р е ш е н и е
Для определения уравнения траектории точки исключим из заданных уравнений движения время t. Из уравнений движения находим выражения соответствующих функций, возводим обе части уравнений в квадрат и складываем:
cos  ; sin ; sin  .
Получим .
Получим
 .
Это уравнение эллипса (рис. К1). Найдем на траектории положение точки М, определив ее координаты при t = 1 с:
xt=1c = –1,59 м;
yt=1c = 1,12 м (рис. К1).
Скорость точки найдем по ее проекциям на координатные оси: .
Это уравнение эллипса (рис. К1). Найдем на траектории положение точки М, определив ее координаты при t = 1 с:
xt=1c = –1,59 м;
yt=1c = 1,12 м (рис. К1).
Скорость точки найдем по ее проекциям на координатные оси:
| 
|
| Рис. К1 |
Vx =  ; Vy =
; Vy =  ; V =
; V =  ,
,
при t = 1 с
Vx = 1,11 м/c; Vy = 1,67 м/c;
V = 2,0 м/c.
Аналогично найдем ускорение точки и определим касательное и нормальное ускорения и радиус кривизны траектории:
 ;
;  ;
;
 ;
;  ;
;  ;
;  .
.
При t = 1 с
a x = 0,87 м/c2; a t = –0,6 м/c2;
a y = –1,30 м/c2; a n = 1,67 м/c2;
a = 1,57 м/c2; r = 2,38 м.
Покажем векторы скорости и ускорения для соответствующей точки М траектории (см. рис. К1).
О т в е т: V = 2,0 м/с; а = 1,57 м/с2; а t= –0,6 м/с2; а n = 1,68 м/с2;
r = 2,38 м.
З а д а ч а К2
Сложное движение точки
Пластина вращается вокруг неподвижной оси по закону j = j(t), заданному в табл. К2. Положительное направление отсчета угла j показано на рисунках дуговой стрелкой (рис. К2.0–К2.9).

| 
|
| Рис. К2.0 | Рис. К2.1 |
На рис К2.7, К2.8, К2.9 ось вращения пластины проходит через точку О1 перпендикулярно плоскости чертежа (пластина вращается в своей плоскости). На рис. К2.0, К2.2, К2.4, К2.5 ось вращения пластины вертикальна, а на рис. К2.1, К2.3, К2.6 – горизонтальна.

|

|
| Рис. К2.2 | Рис. К2.3 |

| 
|
| Рис. К2.4 | Рис. К2.5 |

| 
|
| Рис. К2.6 | Рис. К 2.7 |

| 
|
| Рис. К2.8 | Рис. К2.9 |
По пластине движется точка М согласно закону s = OM = s(t) (табл. К2). На всех рисунках точка М показана в положении, при котором s = ОМ положительно.
Т а б л и ц а К2
| Номер условия | Закон движения пластины j = j (t), рад | Размер R, м | Закон движения точки s = s(t), м |
| 4 (t2 – t) | 1,2 |  R (4t2 – 2t3) R (4t2 – 2t3)
| |
| 3t2 – 8t | 1,6 |  R (2t2 – t3) R (2t2 – t3)
| |
| 6t3 – 12t2 | 1,0 |  R (2t2 – 1) R (2t2 – 1)
| |
| t2 – 2t3 | 1,6 |  R (2t4 – 3t2) R (2t4 – 3t2)
| |
| 10t2 – 5t3 | 0,8 |  R (3t – t2) R (3t – t2)
| |
| 2(t2 – t) | 2,0 |  R (t3 – 2t) R (t3 – 2t)
| |
| 5t – 4t2 | 1,2 |  R (t3 – 2t2) R (t3 – 2t2)
| |
| 15t – 3t3 | 0,8 |  R (t – 2t2) R (t – 2t2)
| |
| 2t3 – 4t | 1,0 |  R (3t2 – 2t) R (3t2 – 2t)
| |
| 6t2 – 3t3 | 2,0 |  R (t – 2t2) R (t – 2t2)
|
Найти абсолютную скорость и абсолютное ускорение точки М в момент времени t = 1с.
Указания. При решении задачи К2 следует движение точки по пластине считать относительным, вращательное движение самой пластины – переносным и воспользоваться теоремами о сложении скоростей и о сложении ускорений.
Прежде всего необходимо определить, где в момент времени t = 1 c будет находиться точка М, и изобразить ее именно в этом положении (а не в произвольном, показанном на рисунке к задаче). В случаях, когда точка М движется по дуге радиуса R, положение точки М определяется углом ОСМ.
Пример решения задачи К2. Пластина (рис. К2) вращается вокруг горизонтальной оси по закону j = j(t). Положительное направление отсчета угла φ показано на рис. К2 дуговой стрелкой. По дуге АОД движется точка М согласно закону s = ОM = s(t); положительное направление отсчета расстояния s – от О к Д.
Д а н о: R = 0,5 м; φ = 2t2; s = ОМ = pR  (φ – в радианах, s – в метрах, t – в секундах).
(φ – в радианах, s – в метрах, t – в секундах).
О п р е д е л и т ь: абсолютную скорость Va и абсолютное ускорение a a точки М в момент времени t = 1 с.

Рис. К2
 Р е ш е н и е
Р е ш е н и е
Точка М совершает сложное движение. При этом ее движение по дуге является относительным, а движение вместе с пластиной – переносным.
Рассмотрим относительное движение. Это движение происходит по закону
 s = ОМ = pR
s = ОМ = pR  . (1)
. (1)
Сначала установим, где будет находиться точка М на дуге AОД в момент времени t = 1с. Подставляя в уравнение (1) t = 1 с, получим  . Тогда
. Тогда  . Изображаем на рис. К2 точку в положении, соответствующем этому углу.
. Изображаем на рис. К2 точку в положении, соответствующем этому углу.
Определим значения скорости и ускорения:


 , (2)
, (2)
где rот = R – радиус кривизны траектории при относительном движении точки. Для момента времени t = 1 c, учитывая, что R = 0,5 м, получим
 ;
;  м/с2;
м/с2;  м/с2. (3)
м/с2. (3)
Положительные значения Vот и  показывают, что вектор
показывают, что вектор  направлен по касательной в сторону положительного отсчета s, а вектор
направлен по касательной в сторону положительного отсчета s, а вектор  так же, как вектор
так же, как вектор  . Вектор
. Вектор  направлен к центру С вдоль радиуса. Покажем эти векторы на рис. К2.
направлен к центру С вдоль радиуса. Покажем эти векторы на рис. К2.
Рассмотрим переносное движение точки. Движение пластины (вращение) происходит по закону φ = 2t2. Найдем угловую скорость ω и угловое ускорение ε переносного вращения:
ω =  = 4t; ε =
= 4t; ε =  = 4.
= 4.
При t = 1 с
ω = 4 с-1; ε = 4 с-2. (4)
Положительные значения указывают на то, что направления ω и ε совпадают с направлением φ (см. рис. К2).
Для определения Vпер и а пер найдем сначала радиус вращения точки М:
KB = h = 2R – R×cos 30° = 0,57 м.
Тогда в момент времени t = 1с, учитывая равенства (4), получим
Vпер = ω × h = 4 × 0,57 = 2,28 м/с;
a врпер = ε × h = 4 × 0,57 = 2,28 м/с2; (5)
a цпер = ω2 × h = 42 × 0,57 = 9,12 м/с2.
Изобразим на рис. К2 вектор скорости  пер с учетом направления ω и векторы ускорений:
пер с учетом направления ω и векторы ускорений:  (направлен по радиусу к оси вращения),
(направлен по радиусу к оси вращения),  (направлен так же, как
(направлен так же, как  пер).
пер).
Ускорение Кориолиса
а кор = 2 | Vот |· |ω | · sin α,
где α – угол между вектором  и вектором
и вектором  , который направлен вдоль оси вращения, как показано на рис. К2, α = 30о.
, который направлен вдоль оси вращения, как показано на рис. К2, α = 30о.
Тогда согласно равенствам (3) и (4) в момент времени t = 1 с
 кор = 2 | Vот | · | ω | sin 30о = 2 · π/4 · 4 · 1/2 = 3,14 м/с2. (6)
кор = 2 | Vот | · | ω | sin 30о = 2 · π/4 · 4 · 1/2 = 3,14 м/с2. (6)
Направление вектора  кор найдем, спроецировав вектор
кор найдем, спроецировав вектор  от на плоскость вращения, и повернув эту проекцию на 900 по ходу вращения пластины (см. рис. К2).
от на плоскость вращения, и повернув эту проекцию на 900 по ходу вращения пластины (см. рис. К2).
Рассмотрим абсолютное движение точки. Определим абсолютную скорость. Так как  а =
а =  от +
от +  пер, а векторы
пер, а векторы  от и
от и  пер взаимно перпендикулярны (см. рис. К2), то в момент времени t = 1 с
пер взаимно перпендикулярны (см. рис. К2), то в момент времени t = 1 с
Vа=  =
=  = 2,4 м/с.
= 2,4 м/с.
Определим абсолютное ускорение. По теореме о сложении ускорений
 а =
а =  . (7)
. (7)
Проведем координатные оси Мxyz (рис. К2) и, проецируя обе части равенства (7) на координатные оси, вычислим проекции векто- ра  а на эти оси. Учтем при этом, что векторы
а на эти оси. Учтем при этом, что векторы  ,
,  лежат на оси х, а векторы
лежат на оси х, а векторы  расположены в плоскости Мyz.
расположены в плоскости Мyz.
Учтя одновременно равенства (3), (5), (6), получим для момента времени t = 1 с
а а x = а кор + а  = 5,42 м/с2;
= 5,42 м/с2;
а а y = – а  соs 60° + а
соs 60° + а  соs 30° = 0,74 м/с2;
соs 30° = 0,74 м/с2;
а а z = - а  соs 60° – а
соs 60° – а  соs 30° + а
соs 30° + а  = 7,27 м/с2.
= 7,27 м/с2.
Тогда
а а =  = 9,1 м/с2.
= 9,1 м/с2.
О т в е т: Vа = 2,4 м/с; а а = 9,1 м/с2.
З а д а ч а к3
Исследование плоскопараллельного движения
твердого тела
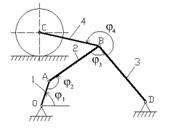
Плоский механизм состоит из стержней 1, 2, 3, 4 и катка с центром С, соединенных между собой шарнирами. На рис. К3.3 и К3.8 стержень 3 шарнирно соединен с ползунами В и Е. На рис. К3.3–К3.8 шарнир D находится в середине соответствующего стержня.
Длины стержней равны соответственно: l 1 = 0,2 м; l 2 = 1,0 м; l 3 = 1,2 м; l 4 = 0,8 м. Радиус катка R = 0,3 м.
Положение механизма определяется углами j1, j2, j3, j4 (рис. К3.0–К3.9). Значения этих углов и скорости звеньев указаны в табл. К3, причем угловая скорость стержня 1 w1 и скорость центра катка VC – величины постоянные.
| 
| |
| Рис. К3.0 | Рис. К3.1 | |

|

| |
| Рис. К3.2 | Рис. К3.3 | |
Определить линейные скорости точек V и угловые скорости звеньев ω, указанные в столбце «Найти» табл. К3.
Построение чертежа следует начинать со стержня, направление которого определяется углом φ1. Дуговыми стрелками на рисунках показано, как откладывать соответствующие углы при построении чертежа механизма

| 
| |
| Рис. К3.4 | Рис. К3.5 | |

| 
| |
| Рис. К3.6 | Рис. К3.7 | |

| 
| |
| Рис. К3.8 | Рис. К3.9 | |
Т а б л и ц а К3
| Номер условия | Углы, град | Заданные скорости | Найти | |||||
| φ1 | φ 2 | φ 3 | φ 4 | ω1, с-1 | VC, м/с | V точек | ω звеньев | |
| – – – – – | – – – – – | В, А С, В В, А С, В В, А С, В В, А С, В В, А С, В | 2 и 3 2 и 4 2 и 3 2 и 4 2 и 3 2 и 4 2 и 3 2 и 4 2 и 3 2 и 4 |
Заданную угловую скорость w1 считать направленной против хода часовой стрелки, а заданную скорость VC – вправо.
Указания. При решении задачи К3 для определения скоростей точек механизма и угловых скоростей его звеньев следует воспользоваться теоремой о проекциях скоростей двух точек тела и понятием о мгновенном центре скоростей, применяя эту теорему (или это понятие) к каждому звену механизма в отдельности.
Пример решения задачи К3. Механизм (рис. К3) состоит из стержней 1, 2, 3, ползуна А и катка, соединенных друг с другом и с неподвижной опорой Е шарнирами.
Д а н о: j1 = 90º; j2 =150º; j3 = 240º; j4 = 150º; l 1 = 1,0 м; l 2 = 0,9 м; l 3 = 1,0 м; ВЕ = 2ДЕ; VC = 4 м/с.
О п р е д е л и т ь: скорости точек VA, VД и угловые скорости звеньев w1, w2.
 Р е ш е н и е
Р е ш е н и е
Строим положение механизма в соответствии с заданными углами (рис. К3).
Определяем скорость точки Д – VД. Точка Д принадлежит стержню СД. Чтобы найти VД, надо знать скорость какой-нибудь другой точки этого стержня и направление вектора 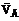 . По данным задачи известны скорость центра катка VC = 4 м/c и направление вектора
. По данным задачи известны скорость центра катка VC = 4 м/c и направление вектора  – параллельно поверхности, по которой катится каток. Направление вектора
– параллельно поверхности, по которой катится каток. Направление вектора 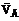 найдем, учтя, что точка Д принадлежит еще и стержню ДВ, вращающемуся вокруг Е; следовательно,
найдем, учтя, что точка Д принадлежит еще и стержню ДВ, вращающемуся вокруг Е; следовательно, 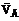 ^ ДВ. Теперь, зная направление векторов
^ ДВ. Теперь, зная направление векторов  и
и 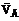 , воспользуемся теоремой о проекциях скоростей двух точек тела (стержня СД) на прямую, соединяющую эти точки. Сначала по этой теореме устанавливаем, в какую сторону направлен вектор
, воспользуемся теоремой о проекциях скоростей двух точек тела (стержня СД) на прямую, соединяющую эти точки. Сначала по этой теореме устанавливаем, в какую сторону направлен вектор 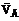 (проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим
(проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим
VC соs 30° = VД; VД = VC соs 30° = 4  = 3,5 м/c.
= 3,5 м/c.

Рис. К3
Определяем скорость точки А – VA. Точка A принадлежит стержню АВ. Следовательно, надо сначала найти скорость точки В, принадлежащей одновременно стержню ВД. Так как стержень ВД вращается вокруг Е, то вектор  ^ ВД и направлен в сторону поворота стержня. Величину скорости VB найдем из пропорции
^ ВД и направлен в сторону поворота стержня. Величину скорости VB найдем из пропорции
 .
.
Так как ВЕ = 2ДЕ, следовательно,
 = 2VД = 2×3,5 = 7 м/c.
= 2VД = 2×3,5 = 7 м/c.
Поскольку точка А принадлежит одновременно ползуну, движущемуся поступательно вдоль направляющих, то линия действия 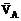 известна. Тогда, зная направление векторов
известна. Тогда, зная направление векторов  и
и 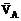 , построим мгновенный центр скоростей (МЦС) стержня АВ; это точка Р1, лежащая на пересечении перпендикуляров к векторам
, построим мгновенный центр скоростей (МЦС) стержня АВ; это точка Р1, лежащая на пересечении перпендикуляров к векторам  и
и 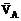 , восстановленных из точек В и А. По направлению вектора
, восстановленных из точек В и А. По направлению вектора  определяем направление поворота стержня АВ вокруг МЦС. Вектор
определяем направление поворота стержня АВ вокруг МЦС. Вектор 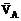 будет направлен в сторону поворота стержня АВ. Учитывая, что
будет направлен в сторону поворота стержня АВ. Учитывая, что
VB = ω1·ВР1; VА = ω1·АР1,
получим
 .
.
Вычислим ВР1 и АР1. Треугольник АР1В – прямоугольный, так как острые углы в нем равны 30º и 60º, и тогда
 м;
м;
BP1 = AР1 sin 30º = 1,2×0,5 = 0,6 м.
В результате  м/c.
м/c.
Определяем величину угловой скорости стержня АВ w1:
 .
.
Определяем величину угловой скорости стержня ВД w2:
 .
.
О т в е т: VA = 14,0 м/c; VД = 3,5 м/c; w1 = 11,7 c-1; w2 = 7,8 c-1.
ДИНАМИКА
З а д а ч а Д1
Дифференциальные уравнения движения
материальной точки
Тело D, имеющее массу m, получив в точке А начальную скорость V0, движется в изогнутой трубе АВС, расположенной в вертикальной плоскости (рис. Д1.0–Д1.9).

| 
|
| Рис. Д1.0 | Рис. Д1.1 |

| 
|
| Рис. Д1.2 | Рис. Д1.3 |

| 
|
| Рис. Д1.4 | Рис. Д1.5 |

| 
|
| Рис. Д1.6 | Рис. Д1.7 |

| 
|
| Рис. Д1.8 | Рис. Д1.9 |
На участке АВ на тело, кроме силы тяжести, действуют постоянная сила  , направленная вдоль трубы, и сила трения. В точке В тело, не изменяя величины своей скорости, переходит на участок ВС и движется, скользя по трубе. При этом на тело, кроме силы тяжести, действуют силы трения и переменная сила
, направленная вдоль трубы, и сила трения. В точке В тело, не изменяя величины своей скорости, переходит на участок ВС и движется, скользя по трубе. При этом на тело, кроме силы тяжести, действуют силы трения и переменная сила  , величина проекции которой Fx на ось х задана в табл. Д1. Там же приведены величины m, V0, Q, расстояние между точками А и В (l = АВ) или tАВ – время движения тела от точки А до точки В и коэффициент трения f тела о трубу.
, величина проекции которой Fx на ось х задана в табл. Д1. Там же приведены величины m, V0, Q, расстояние между точками А и В (l = АВ) или tАВ – время движения тела от точки А до точки В и коэффициент трения f тела о трубу.
Т а б л и ц а Д1
| Номер условия | m, кг | V0, м/с | Q, H | f | l, м | τАВ, c | Fx, H | Найти |
| 2,4 | 0,2 | 1,5 | – | 4 sin (4t) | V1 | |||
| 0,4 | – | 2,5 | –5 cos (4t) | x1 | ||||
| 0,3 | – | 6t | V1 | |||||
| 1,8 | 0,3 | – | –2 cos (2t) | x1 | ||||
| 0,2 | – | –5 sin (2t) | V1 | |||||
| 4,5 | 0,3 | – | 3t | x1 | ||||
| 0,1 | 2,5 | – | 6 cos (4t) | V1 | ||||
| 1,6 | 0,4 | – | –3 sin (4t) | x1 | ||||
| 4,8 | 0,2 | – | 4 cos (2t) | V1 | ||||
| 0,3 | – | 4 sin (2t) | x1 |
Считая тело материальной точкой, необходимо определить закон движения х = (t) на участке ВС.
Указания. Решение задачи Д1 разбивается на две части. Сначала нужно составить и проинтегрировать методом разделения переменных дифференциальное уравнение движения точки D на участке АВ, учитывая начальные условия. Затем, зная время движения на участке АВ (tАВ) или его длину l, определить, какую скорость будет иметь тело в точке В. Эта скорость будет начальной для движения тела на участке ВС. После этого необходимо составить и проинтегрировать дифференциальное уравнение движения на участке ВС тоже с учетом начальных условий.
Пример решения задачи Д1. На вертикальном участке АВ трубы (рис. Д1) на груз массой m действует сила тяжести и постоянная сила сопротивления 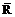 . Длина участка АВ l 1 = 2 м. В точке А груз имеет начальную скоростьV0 = 6 м/с. На наклонном участке ВС на груз действует сила тяжести, сила трения (коэффициент трения груза о плоскость равен f) и переменная сила F = F(t), заданная в ньютонах.
. Длина участка АВ l 1 = 2 м. В точке А груз имеет начальную скоростьV0 = 6 м/с. На наклонном участке ВС на груз действует сила тяжести, сила трения (коэффициент трения груза о плоскость равен f) и переменная сила F = F(t), заданная в ньютонах.
Д а н о: m = 5 кг; R = 40 H; V0 = 6 м/с; l АВ = 2 м; f = 0,2; Fx = 45 sin (3t).
О п р е д е л и т ь: закон движения груза на участке ВС: x = х(t).
 Р е ш е н и е
Рассмотрим движение груза на участке АВ, считая груз материальной точкой. Изображаем груз (в произвольном положении) и действующие на него силы Р е ш е н и е
Рассмотрим движение груза на участке АВ, считая груз материальной точкой. Изображаем груз (в произвольном положении) и действующие на него силы  и и 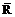 . Проводим ось Az в направлении движения груза и составляем диф- . Проводим ось Az в направлении движения груза и составляем диф-
| 
|
| Рис. Д1 |
ференциальное уравнение движения груза в проекции на эту ось:
 , или
, или  . (1)
. (1)
Далее находим Pz = P = mg, Rz = –R.
При Vz = V получим
 или
или  . (2)
. (2)
Тогда, разделяя в уравнении (2) переменные и интегрируя обе части равенства, приняв g » 10 м/с2, получим
 . (3)
. (3)
Из начальных условий при t = 0 скорость V = V0, что даёт С1 = V0. Тогда уравнение (3) принимает вид
V = 2t + 6. (4)
Учитывая, что 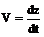 , получим
, получим
 .
.
Откуда при разделении переменных и интегрировании
z = t2 + 6t + C2. (5)
Из начальных условий при t = 0 и начальной координате z0 = 0 находим С2 = 0, следовательно
z = t2 + 6t. (6)
С учётом условий задачи при z = l АВ = 2 м в точке В можно найти время t = τАВ движения груза по участку АВ:
2 = t2 + 6t или t2 + 6t – 2 = 0.
Извлекая корни, получим t1 = 0,3 c; t2 = –6,3 c, в физическом смысле t = τАВ = 0,3 с. Тогда по уравнению (4) скорость в точке В
VB = 2τАВ + 6 = 6,6 м/с. (7)
Теперь рассмотрим движение груза на участке ВС; найденная скорость VB будет для движения на этом участке начальной скоростью (V0 = VB). Изображаем груз (в произвольном положении) и показываем действующие на него силы  ,
,  ,
,  и
и  . Проведём из точки В ось Вx и составим дифференциальное уравнение движения груза в проекции на эту ось:
. Проведём из точки В ось Вx и составим дифференциальное уравнение движения груза в проекции на эту ось:
 . (8)
. (8)
Определим проекции сил на ось х:
Px = P sin 30° = 0,5mg; Nx = 0; Fx = 45 sin (3t);
Fтр x = –fN = – f P cos 30º = – 0,17mg,
тогда уравнение (8) примет вид
 = 0,5mg + 45sin (3t) – 0,17mg = 0,33mg + 45sin (3t). (9)
= 0,5mg + 45sin (3t) – 0,17mg = 0,33mg + 45sin (3t). (9)
Разделив обе части равенства на m = 5кг и принимая g » 10 м/c2, получим
 . (10)
. (10)
Умножая обе части уравнения (10) на dt и интегрируя, найдём Vх:
Vx = 3,3t – 3cos (3t) + C2. (11)
На участке ВС будем отсчитывать время от момента, когда груз находится в точке В, считая в этот момент t = 0. Тогда при t = 0 скорость груза V = V0 = VB = 6,6 м/с. Подставляя эти величины в уравнение (11), получим
С2 = VB + 3cos (0) = 6,6 + 3 = 9,6.
При найденном значении С2 уравнение (11) даёт
 (12)
(12)
Умножая обе части на dt и снова интегрируя, найдём
x = 1,65t2 + 9,6t – sin (3t) + C3. (13)
Так как на участке ВС при t = 0 начальная координата x = 0, то С3 = 0. Окончательно закон движения груза примет вид
x = 1,65t2 + 9,6t – sin (3t), (14)
где x – в метрах, t – в секундах.
О т в е т: x = 1,65t2 + 9,6t – sin (3t).
З а д а ч а Д2
Теоремы о движении центра масс,
об изменении количества движения
и кинетического момента механической системы
Механическая система состоит из прямоугольной вертикальной плиты 1 массой m1 = 20 кг и груза D массой m2 = 6 кг; плита движется вдоль горизонтальных направляющих (рис. Д2.0–Д2.4) или вращается вокруг вертикальной оси Z, лежащей в плоскости плиты (рис. Д2.5–Д2.9). В момент времени t0 = 0 груз начинает двигаться под действием внутренних сил по имеющемуся на плите желобу: закон его движения s = AD = s(t) задан в табл. Д2, где s выражено в метрах, t – в секундах. Форма желоба на рис. Д2.0, Д2.1, Д2.8, Д2.9 – прямолинейная, на рис. Д2.2–Д2.7 окружность радиуса R = 1,2 м с центром в центре масс С1 плиты. Плита, изображенная на рис. Д2.0–Д2.4, имеет при t0 = 0 скорость V0 = 0, на рис. Д2.5–Д2.9 – угловую скорость ω0 = 4 с-1. В это время на плиту начинает действовать вращающий момент или момент сил сопротивления (момент М относительно оси z), заданный в табл. Д2.
Считая груз материальной точкой, следует определить (табл. Д2, столбцы 6, 7) V1 – скорость плиты в момент времени t1 = 1 с; N1 – полную силу нормального давления плиты на направляющие в момент времени t1 = 1 с (указать, куда сила  направлена); ω1 – угловую скорость плиты в момент времени t1 = 1 с;
направлена); ω1 – угловую скорость плиты в момент времени t1 = 1 с;  – угловую скорость плиты как функцию времени.
– угловую скорость плиты как функцию времени.

| 
|
| Рис. Д2.0 | Рис. Д2.1 |

| 
|
| Рис. Д2.2 | Рис. Д2.3 |


| 
|
| Рис. Д2.4 | Рис. Д2.5 |

| 
|
| Рис. Д2.6 | Рис. Д2.7 |
На всех рисунках груз показан в положении, при котором s = AD > 0 (при s < 0 груз будет находиться по другую сторону от точки А).
 
| 
|
| Рис. Д2.8 | Рис. Д2.9 |
Т а б л и ц а Д2
| Номер усло-вия | Закон движения груза Д s = s(t), м | Расстояние до оси Z b, м | Момент сил М, Нм | Найти | ||
| Рис. Д2.0–Д2.1, Д2.8–Д2.9 | Рис. Д2.2–Д2.7 | Рис. Д2.5–Д2.9 | Рис. Д2.0–Д2.4 | |||

| 
| 0,6 | ω1 = f(t) | N1 | ||

| 
| 1,6 | ω1 | V1 | ||

| 
| 1,2 | ω1 = f(t) | N1 | ||

| 
| 1,6 | ω1 | V1 | ||

| 
| 0,6 | ω1 | V1 | ||

| 
| 1,2 | –12 | ω1 = f(t) | N1 |
П р о д о л ж е н и е т а б л. Д2
| Номер усло-вия | Закон движения груза Д s = s(t), м | Расстояние до оси Z b, м | Момент сил М, Нм | Найти | ||
| Рис. Д2.0–Д2.1, Д2.8–Д2.9 | Рис. Д2.2–Д2.7 | Рис. Д2.5–Д2.9 | Рис. Д2.0–Д2.4 | |||
| 0,6t2 | 
| 0,6 | ω1 | V1 | ||

| 
| 1,6 | ω1 | N1 | ||

| 
| 0,6 | –8 | ω1 = f(t) | V1 | |

| 
| 1,6 | ω1 | N1 |
Указания. В задаче, где требуется определить реакцию связи N1, целесообразно воспользоваться теоремой о движении центра масс, а там, где нужно определить скорость тела V1, – теоремой об изменении количества движения. Теорема об изменении кинетического момента применяется в задачах, где нужно найти угловую скорость вращения плиты ω1.
При решении задачи необходимо учесть, что абсолютная скорость  груза складывается из относительной
груза складывается из относительной  и переносной
и переносной  скоростей (определяется так же, как при решении задачи К2), т.е.
скоростей (определяется так же, как при решении задачи К2), т.е.  . Момент инерции плиты относительно оси z, проходящей через центр масс С1 плиты, равен Iz =
. Момент инерции плиты относительно оси z, проходящей через центр масс С1 плиты, равен Iz =  где l – ширина плиты. Для определения момента инерции Iz относительно оси, не проходящей через точку С1 плиты, необходимо воспользоваться теоремой Гюйгенса о моментах инерции относительно параллельных осей.
где l – ширина плиты. Для определения момента инерции Iz относительно оси, не проходящей через точку С1 плиты, необходимо воспользоваться теоремой Гюйгенса о моментах инерции относительно параллельных осей.
Примеры решения задачи Д2. Так как для решения задачи Д2 предусматривается применение различных теорем динамики (см. указания к задаче Д2), рассмотрим ниже три примера с использованием каждой теоремы. Во всех примерах приводится механическая система, состоящая из вертикальной плиты и движущегося в ее плоскости груза D (рис. Д2).


а б

в
Рис. Д2
1. Определение реакции направляющих плиты N. К вертикальной прямоугольной плите массой m1 с помощью невесомого шарнирного стержня BD длиной l прикреплен груз D массой m2 (рис. Д2, а). Плита движется по горизонтальным направляющим без трения. В момент времени t = 0 стержень начинает вращаться в плоскости плиты вокруг точки В, и длина дуги s = AD изменяется по закону
 ,
,
где s – в метрах, t – в секундах.
Д а н о: m1 = 16 кг; m2 = 4 кг; l = 0,5 м.
Н а й т и: реакцию N направляющих в момент времени t = 2 с.
 Р е ш е н и е
Р е ш е н и е
Рассмотрим механическую систему, состоящую из плиты и груза D, и изобразим действующие на нее внешние силы  1,
1,  2 и реакцию
2 и реакцию  . Проведем координатные оси (рис. Д2, а).
. Проведем координатные оси (рис. Д2, а).
Для определения N воспользуемся теоремой о движении центра масс системы и составим дифференциальное уравнение его движения в проекции на ось у:
 (1)
(1)
где m – масса системы; Р1 = m1g; P2 = m2g.
Из формулы, определяющей ординату  центра масс системы, следует, что для рассматриваемой системы
центра масс системы, следует, что для рассматриваемой системы
m ×yC = m1×yC1 + m2×yD. (2)
Если принять высоту плиты равной 2h, то, как видно на рис. Д2, а,
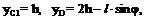
где угол  ,
,
 . (3)
. (3)
Тогда, используя равенства (2) и (3), получим

Вычисляя производные и учитывая, что h = const, получим

Подставив значение  в равенство (1), найдем зависимость N = N(t):
в равенство (1), найдем зависимость N = N(t):
 .
.
Отсюда при t = 2 с определим искомую величину реакции направляющих плиты N = 211,7 Н.
О т в е т: N = 211,7 Н.
2. Определение скорости движени