Изложение численного метода

Методические указания к выполнению контрольной работы

По дисциплине «Применение ЭВМ в тепловых расчетах»

Задания на контрольную работу можно получить на кафедре ТОТиГ или у преподавателя. Номер варианта выдается преподавателем, и необходимо строго придерживаться своего варианта.

Контрольная работа выполняется на листах формата А4 в редакторе Word. Для заметок рецензента оставляются поля и в конце работы несколько чистых страниц. Титульный лист студент оформляет с указанием своей фамилии и инициалов, курса-факультета-номера группы, номера варианта, также указывает должность и фамилию преподавателя, принимающего работу. На последующих страницах обязательно должны быть цель работы, постановка задачи, исходные данные своего варианта, рисунок, краткая теория с основными формулами. Далее нужно представить

1. расчет температурного поля для одного шага по времени с необходимыми пояснениями, применяя метод прогонки.

2. расчет температурного поля для одного шага по времени с необходимыми пояснениями, применяя на выбор один из различных программных продуктов (Mahtcad, он-лайн калькуляторы системы Интернет или др.).

3. график распределения температур в стержне в различные моменты времени (для 5 шагов по времени).

Таблица вариантов

Номер варианта	а∙ 106,м2/с	l,м	t 0,oC	tw1,oC	tw2,oC
	7,5	0,01
	7,5	0,03
	7,5	0,05
	7,5	0,07
	7,5	0,09
	7,5	0,11
	0,1	0,13
	0,1	0,15
	0,1	0,01
	0,1	0,02
	0,1	0,03
	2,5	0,04
	2,5	0,05
	2,5	0,06
	2,5	0,07
	2,5	0,08
	3,6	0,09
	3,6	0,1
	3,6	0,11
	3,6	0,12
	3,6	0,13
	3,6	0,14
		0,15
		0,16
		0,17

Краткая теория

Применение метода конечных разностей по явной схеме (см. лабораторную работу №2), несмотря на его простоту, является не всегда оправданным. Как показывает практика, явная схема является неустойчивой, т.е. при неточном задании краевых условий и промежуточном округлении ошибки будут возрастать при увеличении шага по времени. Поэтому применяют метод конечных разностей, реализуемый по неявной схеме, т.е. когда температуры для последующего момента времени выражаются через одну известную температуру предыдущего момента времени. Данная схема является абсолютно устойчивой, но решается несколько сложнее, чем явная, т.к. приходится решать систему алгебраических линейных уравнений, записанных для всех внутренних узлов тела, где требуется определить температуру. Одно конечно-разностное уравнение связывает только три соседние внутренние узловые точки, следовательно, чтобы определить температуру во всех внутренних точках, нужно составить столько же конечно-разностных уравнений и решать полученную систему уравнений. Существуют различные способы и методы решения систем линейных алгебраических уравнений, некоторыми из них можно воспользоваться в сети Интернет в свободном доступе (напр, онлайн-калькуляторами).

В данной работе для решения одномерных задач нестационарной теплопроводности применяется специальный метод – метод прогонки, который также может быть использован в инженерной практике.

Изложение численного метода

Дифференциальное уравнение нестационарной теплопроводности в случае одномерной задачи имеет вид

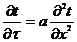. (1)

В лабораторной работе №2 был изложен способ решения дифференциального уравнения теплопроводности (1) методом конечных разностей по явной схеме. Как было указано, решение задач по явной схеме будет устойчивым, если выполняется условие

. (2)

Последнее условие весьма обременительно. Как показывают практические расчеты, при достаточно малых ∆ х и конкретных значениях а величина ∆ τ оказывается очень малой и приходится медленно продвигаться по времени, т.е. делать большое число шагов по времени τ. Все это чрезвычайно повышает трудоемкость решения.

Рассмотрим теперь принципиально другое сеточное уравнение. Если взять приближенное значение производной по времени «назад» (см.рис.1), то получим следующее конечно-разностное соотношение:

. (3)

Уравнение (3) решается труднее, поскольку в него входят три неизвестные температуры: Поэтому в данном случае нужно решать сразу всю систему разностных уравнений типа (3) для всех точек i, k сетки. Здесь так же, как и при решении уравнения Лапласа методом сеток, можно применить метод итераций.

 

Рис.1. Пространственно-временная область одномерной задачи теплопроводности

 

Неявные разностные уравнения решаются сложнее, чем явные, но они абсолютно устойчивы при любом шаге по времени. Это позволяет выбирать шаг ∆ τ значительно большим, чем в явных схемах, и соответственно уменьшать общее время счета всей задачи.

Для реализации численного метода решения задач теплопроводности на ЭВМ разработан специальный метод прогонки, более эффективный, чем метод итераций.

Изложим метод прогонки на примере предыдущей задачи, предложенной в лабораторной работе №2. Уравнение (3) можно, очевидно, записать еще и в виде

(4)

при начальных и граничных условиях:

в момент времени k =0

, (5)

и задана в точках: i =1,2,…, n -1;

(6)

. (7)

Уравнение (4) для удобства дальнейших выводов запишем в виде

, (8)

где .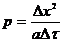

Идея метода прогонки заключается в следующем: связь между двумя соседними узлами и 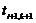представляется в виде

, (9)

где и некоторые коэффициенты, подлежащие определению. Если они будут известны, то делая «прогонку» в направлении справа-налево, начиная с правого граничного условия , можно по (9) последовательно найти все температуры в (k +1)-м слое по времени.

Из (9), заменяя i на i -1, имеем

. (10)

Подставляя (10) в формулу (8), получим

. (11)

Отсюда

. (12)

Сравнивая (12) с (9), получим следующие формулы:

(13)

При i =1 из (8) найдем

. (14)

Или, используя граничное условие (6), из (14) получим

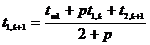. (15)

С другой стороны, из (9) найдем

. (16)

Сравнивая (16) и (15), получим

(17)

Пользуясь системами (А) и (В), производя «прогонку» слева-направо в прямом направлении, последовательно найдем все коэффициенты .

Затем, используя «обратный ход», т.е. прогонку справа-налево, начиная с , как уже было указано, по (9) найдем все температуры в (k +1) слое, если известно распределение температур в k -м слое. Таким образом, указан переход от k -го слоя по времени к (k +1) слою.

Следовательно, отправляясь от известного начального (нулевого) слоя, можно построить решение 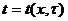во всех точках сетки i, k.

 

ПРИМЕР ОФОРМЛЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ

Титульный лист

«Численное решение одномерных задач нестационарной теплопроводности