ЛАБОРАТОРНАЯ РАБОТА 1
СРАВНЕНИЕ ДВУХ СЕРИЙ ИЗМЕРЕНИЙ
ИСХОДНЫЕ ДАННЫЕ:
Заданы результаты двух серий измерений (две случайные выборки):
1. ПРОЦЕНТ БЕЗРАБОТНЫХ В РАЗВИВАЮЩИХСЯ СТРАНАХ ЗА ОТЧЕТНЫЙ ГОД
1 CEPИЯ ИЗMEPEHИЙ N1= 22 L= 8 8.5 9.4 9.1 9.6 8.1 8.4 7.9 9.2 7.5 8.1 7.7 8.2 5.4 8.8 7.4 8.7 7.6 7.9 7.7 6.2 7.8 10.1
2 CEPИЯ ИЗMEPEHИЙ N2= 34 6.5 6.2 8.1 5.6 9.4 10.3 6.6 7.7 8.7 8.3 3.7 7.7 9.9 6.1 7.9 9.7 6.4 8.8 7.0 11.5 6.4 6.8 5.0 7.0 4.2 8.8 7.3 8.2 6.9 7.2 6.5 8.8 8.2 7.9
РЕШЕНИЕ.
I. ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТОВ.
1. Запишем выборку объема n=n1+n2=22+34=56 в виде группированного статистического ряда. Для этого интервал, содержащий все элементы выборки, разобьем на k непересекающихся интервалов.
В данном случае число интервалов определим по формуле
 .
.
Определим величину интервала группировки:
 .
.
По найденному значению длины интервала рассчитываем границы интервалов. Нижняя граница первого интервала должна быть равна минимальному значению соответствующего признака. Верхняя граница первого интервала факторного признака равна сумме его нижней границы и длины интервала, нижняя граница второго интервала равна верхней границе предыдущего интервала данного признака. Верхняя граница второго интервала больше его нижней границы на длину интервала и т.д.
Вычислим частоты, частости.
Результаты расчетов приводим в следующей таблице:
| номер | Границы | Середина | Частота | Накопленная | Относит. | Нак.отн. | Плотности | |
| интервала | интервалов | интервала | zi | частота | частота | частотa | частот | |
| 3,70 | 4,81 | 4,257143 | 0,035714 | 0,035714 | 1,794872 | |||
| 4,81 | 5,93 | 5,371429 | 0,053571 | 0,089286 | 2,692308 | |||
| 5,93 | 7,04 | 6,485714 | 0,214286 | 0,303571 | 10,76923 | |||
| 7,04 | 8,16 | 7,6 | 0,303571 | 0,607143 | 15,25641 | |||
| 8,16 | 9,27 | 8,714286 | 0,25 | 0,857143 | 12,5641 | |||
| 9,27 | 10,39 | 9,828571 | 0,125 | 0,982143 | 6,282051 | |||
| 10,39 | 11,50 | 10,94286 | 0,017857 | 0,897436 | ||||
| Итого: |
Найдем эмпирическую функцию распределения и построим ее график.
Важной сводной характеристикой выборки является эмпирическая функция распределения ( функция распределения выборки), которая определяется формулой
 ,
,
где  – число наблюдений, при которых значение признака меньше
– число наблюдений, при которых значение признака меньше  ,
,  – объем выборки.
– объем выборки.
В нашем случае, объем выборки по условию равен 56, т.е. n = 56.
Используя рассчитанные накопленные относительные частоты, получаем

График этой функции имеет вид приведен на рис.1.

Рис. 1. График эмпирической функции распределения.
2. Построим гистограмму и полигон частот группированной выборки.
Полигон частот – это ломаная, в которой концы отрезков имеют координаты 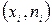 :
:

Рис. 2. Полигон частот.
Гистограмма (статистический аналог плотности) служит для изображения интервальных (непрерывных) статистических рядов и представляет собой ступенчатую фигуру из прямоугольников с основаниями, равными интервалам значений признака и высотами, равными частотам. Если соединить середины верхних оснований прямоугольников отрезками прямой, то можно получить полигон того же распределения.
В нашем случае получаем

Рис.3. Гистограмма.
Гистограмма и полигон являются аппроксимациями кривой плотности (дифференциальной функции) теоретического распределения (генеральной совокупности). Поэтому по их виду можно судить о гипотетическом законе распределения.
3. Найдем моду и медиану объединённой выборки по группированному и негруппированному статистическому ряду.
Мода  для совокупности наблюдений равна тому значению признака, которому соответствует наибольшая частота.
для совокупности наблюдений равна тому значению признака, которому соответствует наибольшая частота.
Для негруппированного статистического ряда:
 (4 раза),
(4 раза),  (4 раза).
(4 раза).
Для интервального ряда моду можно вычислить по формуле
 ,
,
где  означает номер модального интервала (интервал с наибольшей частотой), (
означает номер модального интервала (интервал с наибольшей частотой), ( –1) и (
–1) и ( +1) – номера предшествующего модальному и следующего за ним интервалов.
+1) – номера предшествующего модальному и следующего за ним интервалов.
В примере модальным интервалом является интервал 7,04–8,16 так как наибольшее значение  в этом интервале:
в этом интервале:
 Медиана
Медиана  – значение признака, приходящееся на середину ранжированного ряда наблюдений. Иначе говоря, медиана (выборочная медиана) – это число, которое является серединой выборки, т.е. половина чисел имеет значения большие, чем медиана, а половина чисел имеет значения меньшие, чем медиана. Для ряда с четным числом членов медианой будет полусумма его центральных членов.
– значение признака, приходящееся на середину ранжированного ряда наблюдений. Иначе говоря, медиана (выборочная медиана) – это число, которое является серединой выборки, т.е. половина чисел имеет значения большие, чем медиана, а половина чисел имеет значения меньшие, чем медиана. Для ряда с четным числом членов медианой будет полусумма его центральных членов.
В нашем примере в ряду четное число единиц, поэтому для негруппированного статистического ряда имеем
 .
.
Для интервального ряда медиану следует вычислять по формуле
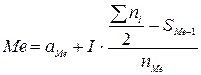 ,
,
где  означает номер медианного интервала, (
означает номер медианного интервала, ( –1) – интервала, предшествующего медианному.
–1) – интервала, предшествующего медианному.
В нашем примере в ряду четное число единиц, поэтому  , следовательно, медианным интервалом является также интервал 7,04–8,16, так как середина вариационного ранжированного ряда (28) находится по накопленным частотам там, где их сумма равна
, следовательно, медианным интервалом является также интервал 7,04–8,16, так как середина вариационного ранжированного ряда (28) находится по накопленным частотам там, где их сумма равна  :
:
 .
.