Решение нелинейного уравнения с одним неизвестным в различных средах программного обеспечения
Методическая разработка по выполнению курсовой работы по информатике для студентов специальности 080801.65 – Прикладная информатика (в менеджменте)
Нижний Новгород
2009
Содержание
Введение............................................................................................................. 3
Постановка задачи......................................................................................... 4
Методы отделения корней............................................................................. 5
Графический метод................................................................................ 5
Аналитический метод............................................................................ 6
Методы уточнения корней............................................................................ 8
Метод половинного деления................................................................. 8
Метод последовательных приближений............................................... 10
Метод Ньютона...................................................................................... 12
Анализ результатов........................................................................................ 16
Заключение........................................................................................................ 17
Варианты заданий............................................................................................. 18
Список рекомендуемой литературы................................................................. 19
Введение
В настоящее время появилось значительное число различных программных продуктов (MathCad, Mathlab и т.д.), с помощью которых, задавая только входные данные и не вникая в сущность алгоритмов, можно решить значительное число задач. Безусловно, умение пользоваться этими программными продуктами существенно сокращает время и ресурсы по решению ряда важных задач.
Зачастую решение некоторых задач сводится к решению достаточно сложных нелинейных уравнений, которые могут представлять собой самостоятельную задачу или являться составной частью более сложных задач. Корни таких уравнений сравнительно редко удается найти точными методами. Кроме того, в некоторых случаях коэффициенты уравнения, полученные в процессе эксперимента или как результаты предварительных расчетов, известны лишь приблизительно. Значит, сама задача о точном определении корней уравнения теряет смысл, и важное значение приобретают способы приближенного нахождения корней уравнения и оценки степени их точности. При традиционном подходе к изучению численных методов в основном в математических курсах ориентируются на стандартные ручные расчеты. С развитием материальной и программной базы современных компьютеров при принятии тех или иных решений более реалистичным представляется подход численных расчетов при использовании новейших информационных технологий.
В представленной работе на примере решения нелинейного уравнения с одной неизвестной f(x)=x+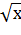 
+ 
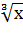-2.5 реализуются 3 технологии:
● алгоритмическая на базе программной среды Pascal;
● с использованием табличного процессора Excel;
● на основе пакета формульных преобразований MathCAD.
Делается сравнительный анализ полученных результатов.
Постановка задачи
Пусть дано уравнение f (x)=0, (1)где функция f (x) непрерывна на некотором множестве X.
Совокупность значений переменной х, при которых уравнение (1) обращается в тождество, называется решением этого уравнения, а каждое отдельное значение – корнем уравнения. В зависимости от вида функции f(x) уравнения подразделяются на алгебраические и трансцендентные.
В первых для получения значения функции по аргументу необходимо выполнить арифметические операции и возведение в степень с рациональным показателем (иррациональные функции, где используется операция извлечения корня, также относят к классу алгебраических функций).
Алгебраическое уравнение можно привести к виду:
+ 
+…+ 
+ 
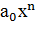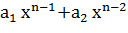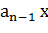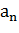=0, (2) где числа 
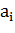, i = 
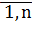- коэффициенты уравнения, которые в общем случае являются комплексными.
Таким образом, корни уравнения могут быть как вещественными, так и комплексными. Будем считать числа 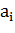вещественными.
Функцию называют трансцендентной, если она содержит логарифмические, показательные, тригонометрические и другие функции. И если в записи уравнения (1) содержится трансцендентная функция, то уравнение называют трансцендентным.
Точные аналитические значения корней уравнения (1) можно найти лишь в простейших случаях (ах+в=0; а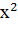 
+вх+с=0; соs(x)=а и т.д.). Кроме того, коэффициенты некоторых уравнений есть приближенные числа, поэтому нельзя говорить о нахождении точных корней.
Будем считать, что уравнение (1) имеет только действительные корни. Тогда нахождение корней с заданной точностью необходимо проводить в два этапа:
- отделение корней, т.е. нахождение достаточно малых промежутков, в которых содержится только один корень уравнения;
- уточнение каждого из отдельных корней, т.е. определение их с заданной точностью.
Рассмотрим технологию выполнения курсовой работы на примере определения корней уравнений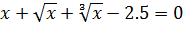 
на интервале 
.
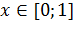Методы отделения (локализации) корней
Графический метод
Он основан на построении графика функции y=f(x). Тогда искомым отрезком [а;в], содержащим корень уравнения (1), будет отрезок оси абсцисс, содержащий точку пересечения графика с этой осью. Иногда выгоднее представить исходную функцию в виде разности двух более простых функций f(x)=g(x)-g1(x) и строить два графика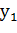 
= g(x) и 
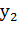= g1(x), точка пересечения которых и является корнем уравнения (1), а отрезок на оси абсцисс с корнем внутри и будет являться интервалом изоляции. Этот метод хорошо работает в случае, если исходное уравнение не имеет близких корней и дает тем точнее результат, чем мельче берется сетка по оси ОХ.
 |
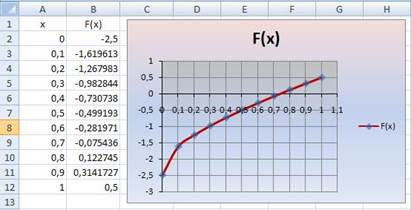Пакет Excel
Первый способ f(x) = x+ 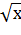+ 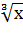-2.5
 |
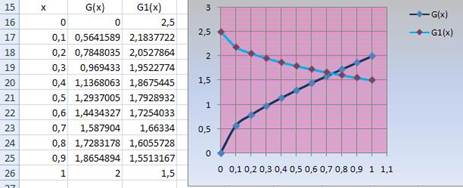Второй способ g(x) = x+
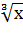; g1(x) = 2.5 -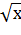
Искомый корень уравнения находится на отрезке [0,7;0,8]
Пакет MathCAD
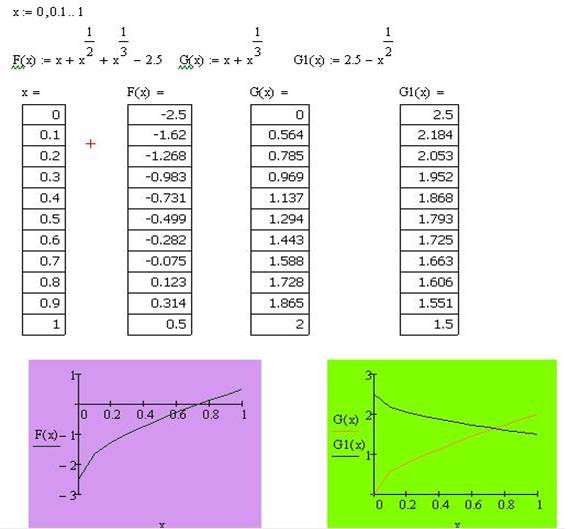
Аналитический метод
Аналитический метод основан на следующем положении: если непрерывная и дифференцируемая на отрезке [a;b] функция f(x) принимает значения разных знаков на его концах (т.е. f(a)∙f(b)<0), то внутри данного отрезка содержится, по крайней мере, один корень уравнения (1), а если к тому же на [a;b] f'(x) сохраняет знак (функция f(x) – монотонная), то этот корень единственный.
Если исходное уравнение имеет близкие корни или функция f(x) сложная, то для выделения отрезков изоляции область изменения аргумента разбивают на отрезки длиной h (шаг) и последовательно проходят их, проверяя значение функции на их концах и выбирая нужные.
Для функции F(x) = x+ 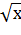+ 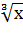-2.5 производная имеет вид F'(x)=1+ 
+ 
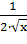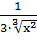Областью допустимых значений аргумента для производной является интервал (0; +∞). При таких значениях аргумента функция F'(x) всегда положительна, следовательно, уравнение имеет единственный корень.
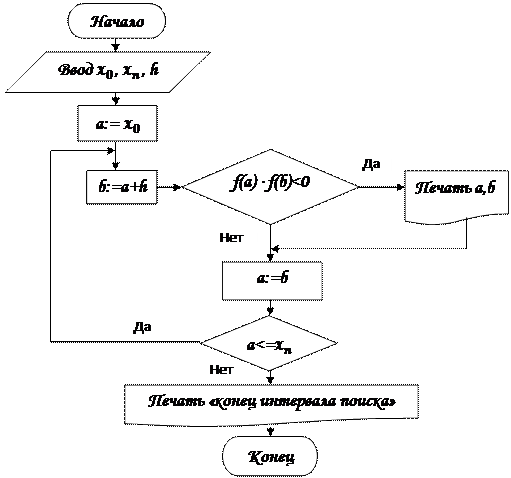Блок-схема
 |
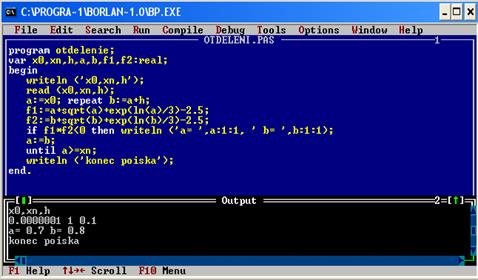Pascal
Методы уточнения корней
Методы отделения корней весьма удобны и просты. Однако они дают ответ только на вопрос локализации корня и позволяют найти его грубое приближенное значение. Если же требуется найти более точное значение корня, то используют различные методы уточнения.