Пример выполнения задания с использованием

ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

 

 

Утверждаю

Проректор-директор ИПР

____________ А.К.Мазуров

«___»__________2011 г.

 

 

ПОРИСТЫЕ АДСОРБЕНТЫ.

КАПИЛЛЯРНАЯ КОНДЕНСАЦИЯ

 

 

 

Методические указания к выполнению расчетной лабораторной работы по дисциплинам «Поверхностные явления и дисперсные системы» и «Коллоидная химия» для студентов ИПР

 

Составители: Михеева Е.В.

 

 

Издательство

Томского политехнического университета

Томск 2011

УДК 541.1(075)

Пористые адсорбенты. Капиллярная конденсация: методические указания к выполнению лабораторных работ по дисциплинам «Поверхностные явления и дисперсные системы» и «Коллоидная химия» для студентов ИПР./Сост. Е.В.Михеева. – Томск: Изд-во Томского политехнического университета, 2011. – 32 с.

 

 

Методические указания рассмотрены и рекомендованы
к изданию методическим семинаром кафедры
физической и аналитической химии ИПР

«__»__________2011 г.

 

 

Зав. кафедрой ФАХ

доктор хим. наук, профессор ____________ А.А. Бакибаев

 

 

Рецензент

Кандидат химических наук, доцент кафедры ФАХ

Н.П. Пикула

 

 

© ГОУ ВПО «Национальный Исследовательский Томский политехнический университет», составление, 2011

© Михеева Е.В., составление, 2011

© Оформление. Издательство Томского политехнического университета, 2011

Пористые сорбенты.

Капиллярная конденсация

 

План коллоквиума

По теме «Адсорбция на границе твердое тело - газ»

1. Адсорбция, основные понятия и определения. Количественные способы выражения величины адсорбции. Физическая и химическая адсорбция. Основные экспериментальные зависимости адсорбции.

2. Теория мономолекулярной адсорбции Лэнгмюра. Основные положения. Уравнение мономолекулярной адсорбции Лэнгмюра (вывод). Анализ и применение уравнения адсорбции Лэнгмюра. Расчет констант в уравнении Лэнгмюра.

3. Эмпирическое уравнение адсорбции Фрейндлиха. Расчет констант в уравнении Фрейндлиха.

4. Теория полимолекулярной адсорбции Поляни. Основные положения. Адсорбционный потенциал. Особенности характеристической кривой.

5. Теория адсорбции БЭТ. Основные положения. Уравнение полимолекулярной адсорбции БЭТ. Расчет констант в уравнении БЭТ. Применение уравнения теории БЭТ к описанию изотерм адсорбции различного вида. Ограничения теории БЭТ.

6. Адсорбция на пористых сорбентах. Классификация пористых сорбентов. Капиллярная конденсация на пористых сорбентах.

Список литературы

1. Фролов Ю.Г. Курс коллоидной химии. Поверхностные явления и дисперсные системы. – М.: Химия, 1989. – С.129-174.

2. Фридрихсберг Д.А. Курс коллоидной химии. – СПб: Химия, 1995. – С.150-178.

3. Воюцкий С.С. Курс коллоидной химии. – М.:Химия, 1976. – С.8-113.

4. Зимон А.Д., Лещенко Н.Ф. Коллоидная химия. – М.: Химия, 1995. – С. 62-64, 68-77, 98-102.

5. Шершавина А.А. Индивидуальные задания по коллоидной химии: учебн.пособие. – Минск: Новое знание, 2008. – С.112 – 126.

Теоретическая часть

Адсорбция – процесс самопроизвольного перераспределения компонентов системы между поверхностным слоем и объемной фазой, то есть поглощение одного вещества поверхностью другого.

С термодинамической точки зрения адсорбция – самопроизвольный процесс выравнивания химических потенциалов компонента в объеме системы и поверхностном слое. Этот процесс происходит вследствие стремления к минимуму поверхностной энергии или энергии Гиббса системы.

Количественные закономерности адсорбции делятся на две группы: закономерности, описывающие адсорбцию на однородных поверхностях, и закономерности для пористых адсорбентов. Это объясняется различием в энергетическом состоянии однородной и пористой поверхностей, и, соответственно, различием в количественном описании протекающих на них процессов адсорбции.

Адсорбция на пористых сорбентах, удельная поверхность которых достигает сотен тысяч квадратных метров, имеет более сложный характер по сравнению с адсорбцией на непористых телах той же химической природы. Как правило, она сопровождается капиллярной конденсацией – конденсацией пара в порах при давлениях меньших, тем давление насыщенного пара адсорбата над плоской поверхностью. Рассмотрим адсорбцию на пористых сорбентах.

Пористые сорбенты

Пористые адсорбенты – твердые тела, внутри которых имеются поры, обуславливающие наличие внутренней межфазной поверхности. Поры могут быть заполнены газом или жидкостью. Тип таких систем Г/Т или Ж/Т. В отличие от адсорбции на телах с ровной поверхностью, адсорбция на пористых телах значительно выше и зависит от строения и размера пор. Увеличение пористости сорбента приводит не только к увеличению удельной поверхности S_уд, но и обеспечивает конденсацию пара при давлениях меньших, чем для ровной поверхности. Кроме того, в микропористых телах наблюдается увеличение энергии адсорбции и резкое возрастание величины адсорбции. По этой причине пористые сорбенты широко применяются в промышленности: в гетерогенном катализе, при улавливании выбросов предприятий (экология) и т.д.

Для количественной характеристики пористых тел используют:

1. Пористость (П) – отношение общего объема пор к общему объему тела:

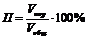. (1)

2. Удельный объем пор (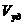) – отношение общего объема пор к массе пористого тела:

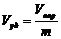. (2)

3. Удельная поверхность (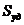) – отношение общей поверхности пор к объему тела:

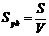. (3)

4. Распределение пор по размерам: интегральные (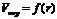) и дифференциальные кривые ().

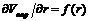Пористые тела классифицируются в соответствии с размерами пор (классификация М.М. Дубинина):

1. Макропористые тела (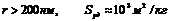). Для количественного описания адсорбции в порах такого размера используют уравнения Лэнгмюра.

2. Мезопористые (переходнопористые) тела (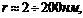 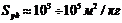). В порах таких адсорбентов идет полимолекулярная адсорбция, которая заканчивается капиллярной конденсацией при образовании вогнутого мениска. Процесс адсорбции описывается теориями Поляни и БЭТ.

3. Микропористые тела (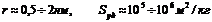) – молекулярные сита (цеолиты – алюмосиликаты, обладающие строго регулярной кристаллической структурой, активированные угли). Процесс адсорбции описывается Теорией объемного заполнения микропор (ТОЗМ) Дубинина.

В случае мезопористых адсорбентов процесс взаимодействия адсорбента с адсорбатом (газом или паром) осложняется капиллярной конденсацией.

Капиллярная конденсация – это конденсация газообразного вещества на пористых твердых телах с размером пор от 2 до 200 нм при давлениях, меньших давления насыщенного пара этого вещества над плоской поверхностью (p_S). Количественно капиллярная конденсация описывается уравнением Томсона (Кельвина):

· для сферических поверхностей: 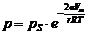, (4)

· для цилиндрических поверхностей: 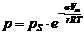, (5)

где р – давление насыщенного пара над вогнутой (искривленной) поверхностью; p_S – давление насыщенного пара над ровной поверхностью; V_m – мольный объем жидкости; σ – поверхностное натяжение жидкости; r – радиус кривизны; R – универсальная газовая постоянная; Т – температура.

Вид изотермы капиллярной конденсации зависит от формы пор. Несмотря на то, что в реальных телах имеются поры различной формы и размеров, процесс капиллярной конденсации можно представить, используя три основные модели:

1) пористое тело с одинаковыми порами конусообразной формы;

2) пористое тело с одинаковыми порами цилиндрической формы с закрытым концом (цилиндрическая закрытая пора);

3) пористое тело с одинаковыми порами цилиндрической формы с открытым концом (цилиндрическая открытая пора);

4) пористое тело с одинаковыми порами бутылкообразной формы с закрытым концом (бутылкообразная закрытая пора).

В порах, имеющих конусообразную форму (рис. 1), в начале адсорбции участки гладкой поверхности и поверхность пор покрываются тонким слоем молекул адсорбата (участок ОА, рис.2)). Как только на дне поры образуется шарообразный мениск, пар начинает мгновенно конденсироваться, происходит мгновенное заполнение поры. По мере заполнения поры радиус мениска увеличивается (уменьшается кривизна), поэтому для дальнейшего заполнения поры необходимо увеличивать давление (участок АВ, рис.2). После того как пора полностью заполнится адсорбатом, дальнейшее увеличение давление на адсорбцию не влияет (участок ВС, рис.2). При уменьшении наблюдается явление десорбции – адсорбат уходит от поверхности адсорбента. Процесс десорбции идет в обратном направлении и описывается той же изотермой.

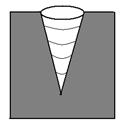Рис.1. Конусообразная пора.	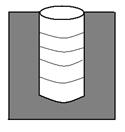Рис.3. Цилиндрическая закрытая пора.
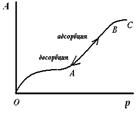Рис. 2. Изотерма капиллярной конденсации на конусообразной поре.	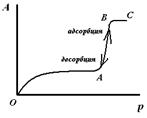Рис. 4. Изотерма капиллярной конденсации на цилиндрической закрытой поре.

В цилиндрических открытых порах (рис.3) конденсация пара также начинается на дне поры, где кривизна сферическая и поэтому наибольшая. Так как в процессе капиллярной конденсации радиус мениска не меняется, пора заполняется конденсатом при постоянном давлении (участок АВ, рис.4), на изотерме капиллярной конденсации прямая вертикальная линия. В этом случае процесс десорбции описывается той же изотермой.

В цилиндрической открытой поре (рис.5) капиллярная конденсация начинается на стенках цилиндра, имеющего кривизну в два раза меньше, чем у сферы того же радиуса (5). Конденсация на стенках цилиндрической поры приводит к уменьшению ее диаметра, что вызывает мгновенное заполнение поры. На концах поры образуются сферические мениски жидкости. Десорбция может начаться только при давлении, соответствующем радиусам кривизны этих менисков, определяемых уравнением (4). Таким образом, опорожнение капилляра происходит при давлении меньшем, чем его заполнение, изотерма десорбции не совпадает с изотермой адсорбции (рис. 6). Этим объясняется появление петли каппилярно-конденсационного гистерезиса.

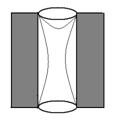Рис.5. Цилиндрическая открытая пора.	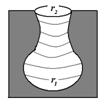Рис.7. Бутылкообразная пора.
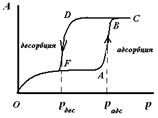Рис. 6. Изотерма капиллярной конденсации на цилиндрической открытой поре	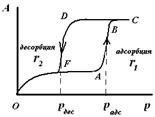Рис. 8. Изотерма капиллярной конденсации на бутылкообразной поре

При смачивании адсорбатом стенок бутылкообразной поры (рис.7), на дне поры образуется вогнутый мениск с радиусом r₁. Так как радиус мениска не меняется, то пора мгновенно заполняется при определенном постоянном значении пара (на изотерме капиллярной конденсации прямая вертикальная линия). Десорбция адсорбата начнется при давлении соответствующем радиусу r₂. Так как r₂ < r₁, то в соответствии с уравнением (4), р_дес < р_адс.

Рис. 9. Изотерма адсорбции при капиллярной конденсации.

Таким образом, опорожнение капилляра будет происходить при давлении меньшем, чем его заполнение (рис.8). Появляется петля капиллярно-конденсационного гистерезиса. Так как реальные сорбенты имеют поры различных форм и размеров, которые заполняются и опорожняются при разных давлениях, то реальные изотермы адсорбции имеют вид, представленный на рис. 9.

 

Для количественного описания адсорбции на мезопористых телах используют теорию полимолекулярной адсорбции Поляни.

В теории Поляни проводится аналогия между адсорбцией и конденсацией пара. Предполагается, что в результате взаимодействия с поверхностью газ сжимается до давления насыщения р_S и переходит в жидкость. При этом возникает адсорбционный объем жидкости 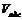, который связан с величиной адсорбции соотношением:

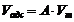, (6)

где А – значение удельной адсорбции в моль/г или моль/кг, 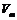– мольный объем адсорбата в конденсированном состоянии (объем 1 моль жидкого адсорбата).

Мерой интенсивности адсорбционного взаимодействия является адсорбционный потенциал, который имеет максимальное значение у поверхности и минимальное – на границе адсорбционного слоя.

Адсорбционный потенциал (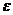) – работа обратимого изотермического процесса по переносу 1 моль адсорбата из данной точки адсорбционного объема в газовую фазу, который рассчитывается по уравнению:

, (7)

где р_S – насыщенное давление газа (пара) при данной температуре (константа для каждого газа), р – равновесное давление в объемной фазе вдали от поверхности.

При заполнении пор адсорбента жидким адсорбатом граница между жидкостью и газом искривляется – возникает капиллярное давление. Приращение энергии Гиббса для искривленной поверхности при постоянной температуре для индивидуального вещества будет равно:

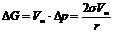, (8)

где 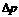– избыточное внутримолекулярное давление, которое для сферических поверхностей согласно уравнению Лапласа равно 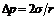; r – радиус кривизны, который из-за малого размера пор совпадает с их радиусом; σ – поверхностное натяжение жидкого адсорбата; V_m – мольный объем жидкого адсорбата, равный отношению молярной массы к плотности жидкого адсорбата.

В состоянии равновесия:

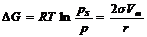. (9)

Кривую капиллярной конденсации (десорбционную ветвь) можно использовать для расчета структурной кривой адсорбента, то есть рассчитать эффективный радиус пор адсорбента, используя уравнение (9):

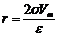. (10)

Для адсорбентов, размер пор которых колеблется в пределах от 2 до 200 нм, предложено уравнение, связывающее адсорбционный объем (пористость) с адсорбционным потенциалом:

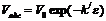, (11)

где 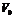– предельный объем пор; 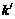– эмпирическая константа.

Уравнение (11) позволяет рассчитать предельный объем пор, для этого уравнение (11) логарифмируют:

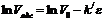. (12)

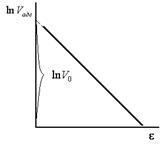Рис.10. Линейная зависимость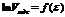

Уравнение (12) представляет собой уравнение прямой в координатах 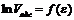(рис.10). Отрезок, отсекаемый прямой на оси ординат равен .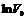

 

Определив по кривой десорбции, строят интегральную кривую распределения пор по размерам в координатах 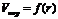, позволяющую определить объем пор определенного радиуса.

Методом графического дифференцирования строят дифференциальную кривую распределения пор по размерам в координатах 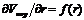. Чем резче выражен максимум и уже дифференциальная кривая, тем меньше различаются поры по размерам. Кроме того, дифференциальная кривая позволяет определить, к какому типу относится данное пористое тело.

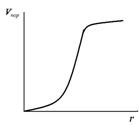Рис. 11. Интегральная кривая распределения пор по размерам

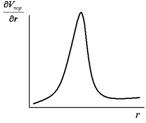Рис. 12. Дифференциальная кривая распределения пор по размерам

 

Пример выполнения задания с использованием