Теорема о перемножении шансов
Теорема 1. Пусть имеется, k групп элементов, причем i-я группа содержит ni элементов, 1<=i<=k. Выберем из каждой группы по одному элементу. Тогда общее число N способов, которыми можно произвести такой выбор, равняется
Урновая схема: выбор без возвращения, с учетом порядка
Общее количество выборок в схеме выбора k элементов из n без возвращения и с учетом порядка определяется числом размещений из n элементов по k элементов.
Урновая схема: выбор без возвращения и без учета порядка
Общее количество выборок в схеме выбора k элементов из n без
возвращения и без учета порядка определяется числом сочетаний из n
элементов по k элементов:
Урновая схема: выбор с возвращением и с учетом порядка
Общее количество выборок в схеме выбора k элементов из n с
возвращением и с учетом порядка определяется числом перестановок из n
элементов:
Урновая схема: выбор с возвращением и без учета порядка
Рассмотрим урну с двумя шариками и перечислим результаты выбора двух шариков из этой урны при выборе с возвращением:
В схеме «без учета порядка» получилось 3 различных результата в
отличие от четырех в схеме «с учетом порядка».Тогда общее количество выборок в схеме выбора k элементов из n с с во звращением и без учета порядка определяется числом сочетаний с повторениями
Гипергеометрическое распределение (урновая схема)
Дискретная случайная величина 
имеет гипергеометрическое распределение, если она принимает значения 
с вероятностями 
представляет вероятность выбора 
объектов, обладающих заданным свойством, из множества 
объектов, случайно извлеченных (без возврата) из совокупности 
объектов, среди которых 
объектов обладают заданным свойством. Ниже приведен пример графика гипергеометрического распределения.
Математическое ожидание и дисперсия случайной величины, имеющей гипергеометрическое распределение с параметрами 
равны:
2/2
Числовые характеристики дискретной случайной величины. Определения моментов. Математическое ожидание и его свойства. Определение и свойства дисперсии. Среднеквадратичное отклонение.
Числовые характеристики дискретной случайной величины.
Основными характеристиками ДСВ являются математическое ожидание, дисперсия и среднеквадратическое отклонение.
Характеристикой среднего значения случайной величины служит математическое ожидание.
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности:
Свойства математического ожидания:
1. Математическое ожидание постоянной величины равно самой постоянной:
2. Постоянный можно выносить за знак математического ожидания:
3. Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей:
4. Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых:
(для разности аналогично)
Характеристиками рассеяния возможных значений случайной величины вокруг математического ожидания служат, в частности, дисперсия и среднее квадратическое отклонение.
Дисперсией случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
Дисперсию удобно вычислять по формуле:
Свойства дисперсии:
1. Дисперсия постоянной равна нулю:
2. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат:
3. Дисперсия суммы (разности) независимых случайных величин равна сумме дисперсий слагаемых:
4. 
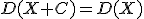
Средним квадратическим отклонением случайной величины называют квадратный корень из дисперсии:
