Теоретические выкладки
Общая теория.
Пусть на отрезке [a, b] ⊂R рассматривается функция f(·)и пусть известны её значения в
(n+ 1) различных узлах: 
принадлежащих [a, b]. Возьмём многочлен степени n
Pn(x)= 
Коэффициенты 
выбираем так, чтобы совпадали значения f(·) и Pn(·) в узлах интерпо-лирования{xi}:
Pn(x)=f(xi), i = 0,1,2,..., n. (2)
Эти равенства дают квадратную систему линейных алгебраических уравнений относительно неизвестных{ai}, причём определитель её суть определитель Вандермонда, что гарантирует существование и единственность решения СЛАУ (2).
Искомый интерполяционный полином может быть представлен в виде
Pn(x)=Ln(x)= 
(3)
Многочлены{ 
}называют множителями Лагранжа
= 
= 
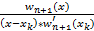
где ωn+1(x) =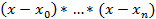 
, а формулу (3) формулой Лагранжа для интерполирующего многочлена Ln(x). Часто интерполяционный полином Ln(·) называют
просто полиномом Лагранжа.
Если считать [a,b]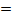 
[−1,1], то учитывая свойства полиномов Чебышева можно утверждать, что ωn+1(x) =Tn+1(x) = 
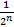Tn+1(x). В общем же случае [a,b] 
[-1;1] достаточно сделать преобразование[a, b]→[−1,1] и получим искомые узлы{xi}в виде:
xi = 
. (6)
Таким образом формула Лагранжа для равноотстоящих узлов примет вид:
Ln(x)= 
где q= 
и h= 
Решение конкретной задачи:
1. Область определения функции 
вся числовая прямая. Возьмем промежуток [-2;2]
2.Будем вычислять узлы полинома с шагом 0.2. Возьмем пять узлов. Для наглядности сравнения результатов по разным формулам будем выводить результат в "Контрольных точках": -0.3, 0.2, 0.75.
3.Будем вычислять узлы полинома также с шагом 0.2. Но возьмем 7 узлов. Будем использовать контрольные точки такие же как в пункте 2.
4.Функция определенана всем интервале. Поэтому мы можем производить построения полинома также в промежутке [-2;2]. Пункты 2-3 для этой функции проведем с аналогичным шагом, количеством узлов и контрольными точками.
Код программы
#include "stdafx.h"
#include <iostream>
#include <fstream>
#include <math.h>
#include <conio.h>
using namespace std;
#define PI 3.14159265
typedef double (*function)(double);//?
void delenie(double *points, double a, double b, int n)//делим на равные отрезки
{
for (int i=0; i<n; i++)
{
points[i]=a+i*(b-a)/(n-1);
}
}
void viborka(double *points, double a, double b, int n)//второй способ выбора точек, через формулу
{
for (int i=0; i<n; i++)
{
points[i]=cos(PI*(2*i+1)/(2*n))*(b-a)/2+(b+a)/2;
}
}
double polinom(double x, int k, double *points, int n)
{
double result=1;
for (int i=0; i<n; i++)
{
if (i!=k)
{
result=result*(x-points[i])/(points[k]-points[i]);
}
}
return result;
}
double L4(function f, double *points, double x, int n)
{
double result = 0;
for (int i = 0; i < n; i++)
{
result =result + f(points[i]) * polinom(x,i,points,n);
}
return result;
}
double func(double x)
{
return sqrt(x)-cos(x); //my function
}
int main()
{
double a=0, b=2, step; //my interval
int n, m=3;
cout<<"Count of points: ";
cin>>n;
cout<<"Interpolation step: ";
cin>>step;
double *checkpoints=new double[m], *delenie_points=new double[n], *viborka_points=new double[n];
checkpoints[0]=0.0; //my checkpoints
checkpoints[1]=0.2;
checkpoints[2]=0.75;
delenie(delenie_points,a,b,n);
viborka(viborka_points,a,b,n);
cout<<"x f(x) L4_R(f,x) L4_0f(x)"<<endl;
for (double x=a; x<=b; x+=step)
{
cout<<x<<" "<<func(x)<<" "<<L4(func,delenie_points,x,n)<<" "<<L4(func,viborka_points,x,n)<<endl;
}
cout<<"two"<<"xk"<<" "<<"f(xk)"<<" "<<"L4(equidistant_nodes,xk) L4(optimal_nodes,xk)"<<endl;
for (int i=0; i<3; i++)
{
cout<<checkpoints[i]<<'\t'<<func(checkpoints[i])<<'\t'<<L4(func,delenie_points,checkpoints[i],n)<<'\t'<<L4(func,viborka_points,checkpoints[i],n)<<endl;
}
system ("pause");
return 0;
}
Результат работы программы
1)
Функция: f(x) =x3-ex+ 1
Количество узлов: 5
Шаг интерполяции: 0.2
| xk | f(xk) | Равностоящие узлы | Корни полинома Чебышева | |
| -0.3 | -0.767818 | -0.77737 | -0.78005 | |
| 0.2 | -1.2134 | -1.20603 | -1.20409 | |
| 0.75 | -1.69513 | -1.68311 | -1.67512 |
2)
Функция: f(x) =x3-ex+ 1
Количество узлов: 7
Шаг интерполяции: 0.2
| xk | f(xk) | Равностоящие узлы | Корни полинома Чебышева | |
| -0.3 | -0.767818 | -0.767672 | -0.767452 | |
| 0.2 | -1.2134 | -1.21353 | -1.21369 | |
| 0.75 | -1.69513 | -1.69504 | -1.69533 |
3)
Функция: f(x) =|x|*(x3-ex+ 1)
Количество узлов: 5
Шаг интерполяции: 0.2
| xk | f(xk) | Равностоящие узлы | Корни полинома Чебышева | |
| -0.3 | -0.230345 | 0.33681 | 0.429212 | |
| 0.2 | -0.242681 | -0.383531 | -0.435411 | |
| 0.75 | -1.27134 | -1.46913 | -1.61739 |
4)
Функция: f(x) =|x|*(x3-ex+ 1)
Количество узлов: 7
Шаг интерполяции: 0.2
| xk | f(xk) | Равностоящие узлы | Корни полинома Чебышева | |
| -0.3 | -0.230345 | -0.0186585 | 0.0572008 | |
| 0.2 | -0.242681 | -0.190799 | -0.214685 | |
| 0.75 | -1.27134 | -1.28847 | -1.26448 |
Список литературы
1.Методические указания по практикуму работы на ЭВМ, А.П. Иванов, Л.Т.Позняк
2. https://ru.wikipedia.org/
3.Численные методы, Н.С. Бахвалов, Н.П. Жидков, Г.М.Кобельков