При расчете устойчивости сжатых составных стержней относительно оси у-ов учет влияния податливости связей производится путем определения приведенной гибкости. Приведенную гиб-

Рис. 89. Типы составных сжатых стержней: а-пакетного профиля; б-с короткими прокладками; в, г-стержни, часть ветвей которых не оперты в концах
кость таких стержней относительно оси у-ов - Лу определяют, исходя из общей формулы с введением поправочного коэффициента кj к моменту инерции за счет податливости связей. Приведенная гибкость составного стержня равна:

по нормам обозначен через и тогда
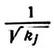
где коэффициент
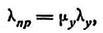
где My - коэффициент проведения гибкости, величина которого меньше единицы (ki<1).
Для всех составных стержней, приведенных на рис. 89, с учетом возможной деформации отдельных ветвей между точками их закрепления, приведенная гибкость относительно оси у в общем случае примет следующее выражение:
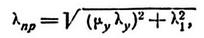
где
· Лу - гибкость всего стержня относительно оси у-ов, вычисленная по расчетной длине его /о -без учета податливости соединений;
· Л1 - гибкость отдельной ветви относительно оси 1-1, вычисленная по расчетной длине l1 (расстоянию между связями);
· My - коэффициент приведения, который определяется по формуле (61);
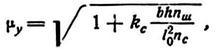
где b - полная ширина поперечного сечения элемента в см в плоскости изгиба; h - полная высота поперечного сечения в см; 10 - расчетная длина стержня в м (см. раздел III § 14); nc - расчетное число срезов связей в одном шве на 1 м элемента;
nш - расчетное число швов в элементе; при наличии нескольких швов с различным числом срезов принимается среднее для всех швов число срезов; кс - коэффициент податливости связей, величина которого дана в табл. 13, в зависимости от диаметра нагеля (d) в см.
|
|
В практике проектирования деревянных конструкций наиболее часто встречаются следующие основные типы составных стержней, для которых в отношении оси у-у имеем:
1) Стержень-пакет (рис. 89,а).
Приведенная гибкость определяется по формуле (60) при Л1 = 0: Лпр = My*Лц где Лц определяется по J6p и Fбр для всего сечения стержня.
2) Стержень с короткими прокладками (рис. 89,б).
Расчетная гибкость определяется по формуле (60), в которой Л1 - гибкость отдельной ветви относительно оси 1-7, определенная -по расчетной длине ветви l1, равной расстоянию между крайними связями прокладок, причем, если l1меньше семи толщин ветви, то принимается Л1 = 0. Расчетная площадь равна площади ветвей без учета прокладок.
3) Стержень, часть ветвей которого не оперта (рис. 89, в, г).
Расчетная гибкость определяется по формуле (60), как для пакетов (при Л1 = 0), но при условии, что Jу определяется для всех опертых и неопертых ветвей.
Устойчивость относительно оси х-ов стержней-пакетов (рис. 89, а) и стержней с короткими прокладками (рис. 89, б) не зависит от сдвига в швах и производится по правилам, установленным для стержней цельного сечения.
Коэффициенты податливости связей кс
Для стержней, часть ветвей которых не оперта, расчетный момент инерции относительно оси x-ов определяется с учетом неполного включения в работу неопертых ветвей за счет податливости связей, а именно:

где
J0 - момент инерции поперечного сечения опертых ветвей; Jно- момент инерции поперечного сечения неопертых ветвей. Радиус инерции относительно оси х-ов находится по формуле:
|
|
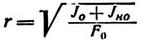
где F0 - площадь поперечного сечения опертых ветвей.
Расчетная площадь поперечного сечения стержня при центральном сжатии определяется только для опертых ветвей.
Дальнейший расчет таких стержней на устойчивость при центральном сжатии ведется по правилам, установленным для стержней цельного сечения.