Задача 1.
Из данной совокупности секвенций выбрать доказуемые, построить их доказательства, для недоказуемых показать их недоказуемость с помощью: а) алгоритма Квайна, б) алгоритма редукций, в) метода резолюций. Среди этих доказательств недоказуемости выбрать оптимальное в каждом конкретном случае.
а) x  y, x
y, x  y, y
y, y  z ├ u
z ├ u  z
z
б) ├ (x  y)
y)  (x
(x  y)
y)
в) x  y,
y, 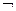 x
x  z, u
z, u  (x
(x  z) ├ (u
z) ├ (u  y)
y)  z
z
г) y├ (y  x)
x)  x
x
Решение.
а) Проверим доказуемость с помощью таблицы истинности.
| x | y | z | u | x  y y
| x  y y
| y  z z
| 1  2 2
| 4  3 3
| u  z z
| 5  6 6
|
Данная формула доказуема. Построим доказательство по правилам вывода.
y├ y z├ z

 12 12 4
12 12 4
x├ x y, x├ y z, y├ z; z├ (u  z)
z)


 4 7 7
4 7 7
x├ (x  y) y├ (x
y) y├ (x  y) z├ (y
y) z├ (y  z); z├ (u
z); z├ (u  z)
z)
 12
12
x, y, z├ (x  y); x, y, z├ (x
y); x, y, z├ (x  y); x, y, z├ (y
y); x, y, z├ (y  z); x, y, z├(u
z); x, y, z├(u  z)
z)
 1
1
x, y, z├ (x  y)
y)  (x
(x  y)
y)  (y
(y  z); ├ x, y, z
z); ├ x, y, z  (u
(u  z)
z)
8 
(x  y)
y)  (x
(x  y)
y)  (y
(y  z)├ (u
z)├ (u  z)
z)
б) ├ (x  y)
y)  (x
(x  y) =(x
y) =(x  y)
y)  (x
(x  y) // (по аксиоме)
y) // (по аксиоме)
| x | y | x  y y
| x  y y
| (x  y) y)  (x (x  y) y)
|
Доказательство
x├ x; y├ y x├ x
 |  |
x, y├ x; x, y├ y x, y├ x


 x, y├ (x
x, y├ (x  y) x, y├ (x
y) x, y├ (x  y)
y)
(x  y)
y)  (x
(x  y)
y)
в) x  y,
y, 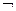 x
x  z, u
z, u  (x
(x  z) ├ (u
z) ├ (u  y)
y)  z
z
| X | y | z | u | x  y y
| 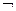 x x
| 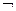 x x  z z
| x  z z
| u  4 4
| 1  3 3
| 6  5 5
| u  y y
| 8  z z
| 7  9 9
|
Покажем недоказуемость с помощью
1) Алгоритма Квайна:
((x  y)
y)  (
(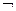 x
x  z)
z)  (u
(u  (x
(x  z)))
z)))  ((u
((u  y)
y)  z)
z)
x=0
(y  u)
u)  ((u
((u  y)
y)  z)
z)
y=0 y=1
0  (u
(u  z)=1. u
z)=1. u  (u
(u  z)
z)
z=0 z=1
u 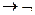 u u
u u  1=1
1=1
u=0 u=1
 0
0  1=1 1
1=1 1  0=0
0=0
2)Алгоритма редукций:
предположим, что
((x  y)
y)  (
(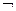 x
x  z)
z)  (u
(u  (x
(x  z)))
z)))  ((u
((u  y)
y)  z)=0, т.е. предположим, что формула недоказуема, тогда
z)=0, т.е. предположим, что формула недоказуема, тогда
((x  y)
y)  (
(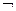 x
x  z)
z)  (u
(u  (x
(x  z)))=1 ((u
z)))=1 ((u  y)
y)  z)=0
z)=0
значит: u  y=1, z=0
y=1, z=0
отсюда: u=1,y=1, z=0;
x  y=1,
y=1, 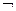 x
x  z=1, u=1, x
z=1, u=1, x  z=1
z=1
x  0=1, значит x=0
0=1, значит x=0
0  1=1,
1=1, 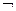 0
0  0=1.
0=1.
Противоречий нет. Формула недоказуема.
Наиболее оптимальным является алгоритм редукций.
г) y├ (y  x)
x)  x
x
| x | y | y  x x
| 1  x x
| y  2 2
|
Для доказательства воспользуемся эквивалентностями ИВ:
(φ  ψ)
ψ) 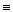 (
(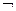 φ
φ  ψ);
ψ); 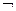 (φ
(φ  ψ)
ψ) 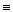 (
(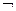 φ
φ 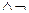 ψ);
ψ);
(φ  (ψ
(ψ  χ))
χ)) 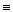 (φ
(φ  ψ)
ψ)  (φ
(φ  χ).
χ).
Преобразуем
(y  x)
x)  x
x 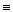
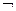 (y
(y  x)
x)  x
x 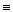
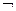 (
(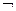 y
y  x)
x)  x
x 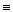 (y
(y 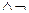 x)
x)  x
x 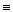 (y
(y  x)
x)  (
(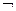 x
x  x)
x) 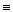 y
y  x
x
Получаем: y├ y  x
x
Строим доказательство
y├ y
 4
4
y├ y  x
x
Задача 2.
Найти формулу исчисления предикатов истинную на алгебраической системе α и ложную на системе δ.
α =<R;∙>  δ =<N;∙>
δ =<N;∙>
Решение
Истинной на системе α и ложной на системе δ будет формула
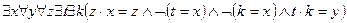
Задача 3.
Построить доказательство формулы в исчислении предикатов

Доказательство
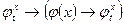 - аксиома 1
- аксиома 1

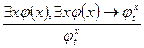
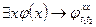
 - аксиома 14
- аксиома 14
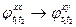
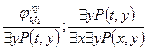
Задача 4.
Установить, выполнима ли следующая формула и если выполнима, то построить модель этой формулы.
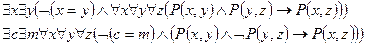

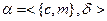
Задача 5.
Привести к пренексной и клазуальной нормальным формам следующую формулу:

Решение:
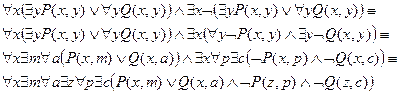
Задача 6.
Методом резолюций проверить, противоречиво ли множество предложений {Φ1, Φ2, Φ3}. Если множество не противоречиво, то построить модель этого множества.

Решение:
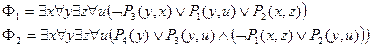

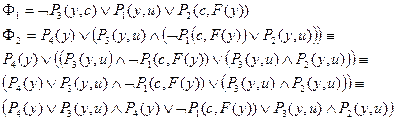

Т.к. множество формулы {Ф1, Ф2} непротиворечиво 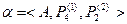
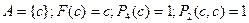
Задача 7.
Доказать примитивную рекурсивность функции, выражая ее через простейшие с помощью операторов суперпозиции и примитивной рекурсии.
f(x, y)=x∙y+1
Доказательство
Считаем sum(x,y) – примитивная рекурсия.
mult(x,y)=x∙y
mult(x,0)=0
mult(x,y+1)=x∙(y+1)=x∙y+x=mult(x,y)+x=sum(mult(x,y),x)


Задача 8.
Построить машину Тьюринга для вычисления функции
f(x, y)=x∙y+1
Решение
| q | q0 | q1 | q2 | q3 | q4 | q5 | q6 | q7 | q8 |
| 0Rq1 | 1Rq2 | 1Rq2 | 0Rq4 | 1Rq4 | 1Rq5 | 1Lq6 | 1Lq8 | 1Lq9 | |
| 0Rq13 | 0Rq3 | 0Rq5 | 1Lq6 | 0Lq7 | 0Lq15 | 1Lq10 |
| q9 | q10 | q11 | q12 | q13 | q14 | q15 | q16 | q17 |
| 1Lq9 | 1Rq11 | 0Lq12 | 1Lq12 | 0Rq13 | 0Lq16 | 0Lq16 | ||
| 0Rq3 | 1Lq10 | 1Rq0 | 1Lq14 | 0Lq15 | 0Rq17 | 0Rq |
Задание №1
Из данной совокупности секвенций выбрать доказуемые, построить их доказательства, для недоказуемых показать их недоказуемость с помощью:
А) Алгоритма Квайна,
Б) Алгоритма редукции,
В) Метода резолюций.
Среди этих доказательств недоказуемости выбрать оптимальный в каждом конкретном случае.
1) x, y, yÚu, uÚxÚØz |- uÚz
2) |- (x®((yÚx) ® z)) ® (y®z)
3) xÚy |- (zÙx) ® (yÙz)
4) Øx, Øy |- (x ® z) ® (y ®z)
Решение:
Секвенция 1) – недоказуема.
Проверка:
а) Алгоритм Квайна:
xÙyÙ(yÚu)Ù(uÚxÚØz) |- uÚz
Пусть x = 1, тогда:
yÙ(yÚu)Ù(uÚØz) |- uÚz
Пусть y=1, тогда:
1Ù1Ù(uÚØz) |- uÚz
Пусть u=0, тогда:
1Ù0ÙØz |- 0Úz
Пусть z=0 тогда:
1 |- 0 – тождественно ложно => секвенция недоказуема
б) Алгоритм редукции:
Предположим: xÙyÙ(yÚu)Ù(uÚxÚØz) ® uÚz = 0
Тогда xÙyÙ(yÚu)Ù(uÚxÚØz)=1, uÚz=0 => u=0, z=0.
Подставим u=0, z=0 в xÙyÙ(yÚu)Ù(uÚxÚØz)=1:
Обязательно должно быть (uÚxÚØz)=1
(0ÚxÚ1)=1
1=1 => непротиворечиво => секвенция недоказуема
в) Метод резолюции (оптимальный):
Докажем противоречивость:
xÙyÙ(yÚu)Ù(uÚxÚØz), Ø(uÚz)
Приводим к КНФ:
x, y, (yÚu), (uÚxÚØz), Øu,Øz
(1) x
(2) y
(3) yÚu
(4) uÚxÚØz
(5) Øu
(6) Øz
(7) resu(3,5) = y
Данное множество непротиворечиво => секвенция недоказуема.
Секвенция 2) – недоказуема.
Проверка:
а) Алгоритм Квайна:
|- (x®((yÚx) ® z)) ® (y®z)
Пусть x = 0, тогда:
|- (0®((yÚ0) ® z)) ® (y®z)
Пусть y=1, тогда:
|- (0®((1) ® z)) ® (1®z)
Пусть z=0, тогда:
|- 0 ® 0
1 |- 0 – тождественно ложно => секвенция недоказуема
б) Алгоритм редукции (оптимальный):
Предположим: |- (x®((yÚx) ® z)) ® (y®z) = 0
Тогда (x®((yÚx) ® z)) ® (y®z) = 0 => x=0, y=1, z=0.
Подставим x=0, y=1, z=0 в 1:
0=0 или
1=1 => непротиворечиво => секвенция недоказуема
в) Метод резолюции:
Докажем противоречивость:
Ø (x®((yÚx) ® z)) ® (y®z)
Приводим к КНФ:
Ø ((x®(Ø(yÚx) Ú z)) ® (y®z))
Ø (Ø(ØxÚ(Ø(yÚx) Ú z)) Ú (ØyÚz))
Ø ((ØØxÙ(ØØ(yÚx) Ù Øz)) Ú (ØyÚz))
Ø ((xÙ yÙx ÙØz)) Ú (ØyÚz))
Ø ((xÙ yÙØz)) Ú (ØyÚz))
Ø (xÙ yÙØz) ÙØ(ØyÚz)
(ØxÚØyÚz)Ù(yÙØz)
(1) (ØxÚØyÚz)
(2) y
(3) Øz
(4) resy(1,2) = (ØxÚz)
(5) resz(1,3) = (ØxÚØy)
Данное множество непротиворечиво => секвенция недоказуема.
Секвенция 3) –недоказуема.
Проверка:
а) Алгоритм Квайна(оптимальный):
xÚy |- (zÙx) ® (yÙz)
Пусть x = 1, тогда:
1Úy |- (zÙ1) ® (yÙz)
Пусть y=0, тогда:
1 |- z ® 0
Пусть z=0, тогда:
1 |- 0 – тождественно ложно => секвенция недоказуема
б) Алгоритм редукции:
Предположим: xÚy |- (zÙx) ® (yÙz) = 0
Тогда xÚy =1, (zÙx) ® (yÙz) = 0
Тогда (zÙx)=1, (yÙz) = 0 => z=1, x=1, y=0
Подставим z=1, x=1, y=0 в xÚy =1:
Обязательно должно быть (1Ú0)=1
1=1 => непротиворечиво => секвенция недоказуема
в) Метод резолюции:
Докажем противоречивость:
xÚy, Ø((zÙx) ® (yÙz))
Приводим к КНФ:
xÚy, Ø(Ø(zÙx)Ú (yÙz))
xÚy, (ØØ(zÙx)Ù Ø(yÙz))
xÚy, z,x, (ØyÚØz)
(1) xÚy
(2) z
(3) x
(4) (ØyÚØz)
(5) resy(2,4) =Øy
(6) resy(1,5) =x
Данное множество непротиворечиво => секвенция недоказуема.
Секвенция 4) – доказуема.
Проверка:
По формулам вывода:
0 |- z = > тождественно истина => секвенция доказуема
Для док-ва воспользуемся эквив-тями ИП:
(j®y)º(ØjÚy), Ø (jÚy)º(ØjÙØy),
jÚ (yÙx)º (jÚy)Ù (jÚx)
преобразуем:
(x®z)®(y®z) ºØ(x®z)Ú(y®z)ºØ(ØxÚz)Ú(ØyÚz)º(xÙØz)Ú(ØyÚz) º º (x ÚØy Úz) Ù (Øz ÚØy Úz) ºx ÚØy Úz
получили:
Øx, Øy |-x ÚØyÚ z
аксиома:
Ø y |- Ø y 11,12
Øx, Øy|- Ø y 5
Øx, Øy |- x ÚØy 4
Øx, Øy |- x ÚØy Ú z
Задание №2