Методом резолюций проверить, противоречиво ли множество предложений

{Ф₁ , Ф₂ , Ф₃}. Если множество непротиворечиво, то построить модель этого

множества.

Ф₁ = х (у Р₁(х,у) Λ у (Р₁(х,у) → Р₂(у,х)))

Ф₂ = х (у Р₁(х,у) Λ z Р₂(х,z))

Ф₃ = x y z u (Р₂(х,у) Λ Р₁(y,z) Λ Р₁(z,u))

РЕШЕНИЕ.

Ф₁ = х (у Р₁(х,у) Λ у (Р₁(х,у) → Р₂(у,х))) ≡

≡ х у (Р₁(х,С₁) Λ (Р₁(х,у) → Р₂(у,х))) ≡

≡ у (Р₁(С₂,С₁) Λ (Р₁(С₂,у) → Р₂(у, С₂))) ≡

≡ у (Р₁(С₂,С₁) Λ (Р₁(С₂,у) v Р₂(у, С₂)))

Ф₂ = х (у Р₁(х,у) Λ z Р₂(х,z)) ≡ х (Р₁(х,С₁) Λ Р₂(х,С₃))

Ф₃ = x y z u (Р₂(х,у) Λ Р₁(y,z) Λ Р₁(z,u)) ≡

≡ х z (Р₂(х,f(x)) Λ Р₁(f(x),z) Λ Р₁(z,f(z)))

{ Р₁(С₂,С₁); Р₁(С₂,у) v Р₂(у, С₂); Р₁(х,С₁); Р₂(х,С₃); Р₂(х,f(x)); Р₁(f(x),z); Р₁(z,f(z))}

res (1, 2) = Р₂(у, С₂)

C₁/y

Множество непротиворечиво. Построим модель этого множества.

Задача №10.

Доказать примитивную рекурсивность функции, выражая их через простейшие с

помощью операторов суперпозиции и примитивной рекурсии.

.

x − 3, при x > 3

f(x) =

0, при x ≤ 3

РЕШЕНИЕ.

f(x) = x − 3

f₁(x) = x − 1

0, при x ≤ 1

f₁(x) =

x − 1, при x > 1

 

f₁(0) = 0

f₁(x + 1) = x

f₁(x) – примитивно - рекурсивная функция

f(x) = f₁(x) ◦ f₁(x) ◦ f₁(x) - суперпозиция

f(x) – примитивно - рекурсивная функция

Задача №11.

Построить машину Тьюринга для вычисления функции из задачи №10.

 

РЕШЕНИЕ.

x − 3, при x > 3

f(x) =

0, при x ≤ 3

 

q₁ 1 → q₁ 0

q₁ 0 → R q₂

q₂ 1 → q₂ 0

q₂ 0 → R q₃

q₃ 1 → q₃ 0

q₃ 0 → R q₄

q₄ 0 → q₄ 1

q₄ 1 → q₀

 

19Задача 1. Из данной совокупности секвенций выбрать доказуемые, построить их доказательства, для недоказуемых показать их недоказуемость с помощью: а) алгоритма Кванта, б) алгоритма редукции, в) метода резолюций. Среди этих доказательств недоказуемости выбрать оптимальное в каждом конкретном случае.

Решение:

а)

Доказуема

 

б)

Недоказуема, покажем это по алгоритму редукции.

Формула будет неверна при следующих условиях:

в)

Недоказуема, покажем это по алгоритму Квайна:

Возьмем переменные по убыванию: x,z,y,u

Встретили 0, следовательно, формула недоказуема.

 

г)

Доказуема:

Задача 2. Найти формулу исчисления предикатов истинную на алгебраической системе А и ложную на системе В

А=<Q;+>, B=<Z;+>

 

Решение:

Задача 3. Построить доказательство формулы в исчислении предикатов

Решение:

Докажем формулу в одну сторону:

 

Докажем формулу в другую сторону:

Задача 4. Установить выполнима ли следующая формула и если выполнима, то построить модель этой формулы.

Решение:

y=f(x)

z=g(x)

 

Формула выполнима, ее модель:

x	f(x)	g(x)
a	a	b
b	b	a

 

P	a	b
a	+	+
b	+	+

 

Задача 5. Привести к пренексной и клазуальной формам следующую формулу

Решение:

x=f(t,m)

y=g(t,m)

z=h(t,m)

k=s(t,m)

Ответ:

Задача 6. Методом резолюций проверить, противоречиво ли множество предложений {Ф₁,Ф₂,Ф₃}. Если множество непротиворечиво, то построить модель этого множества.

Решение:

x=k(y)

 

x=g(y)

z=t(y)

 

z= m(x,y)

 

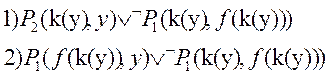
Множество непротиворечиво, его модель:

x

a

b

 

y	k(y)	g(y)	t(y)
a	b	b	b
b	a	a	a

 

m(x,y)	a	b
a	a	b
b	b	a

 

c	f(c)
a	b
b	a

 

P1(a,b)	a	b
a	+	-
b	-	+

 

P2(a,b)	A	b
a	-	+
b	+	-

 

P(a,b)	a	b
a	+	-
b	-	+

 

Задача 7. Доказать примитивную рекурсивность функций, выражая их через простейшие с помощью операторов суперпозиции и примитивной рекурсии

f(x,y)=xy+1

Решение:

Задача 8. Построить машины Тьюринга для вычисления функций из Вашей задачи №7

Решение:

X+1 Y+1
…..			…..				…..			….
	Q1

 

q₁1 → q₁R уменьшаем

q₁0 → q₂L массив единиц X на 1

q₂1 → q₃0

q₃0 → q₄L

q₄1 → q₄L

q₄0 → q₅R проверяем был ли X равен 0

q₅0 → q₆0 -----если Х=0, то

q₆0 → q₆R идем на первую 1 Y’а

q₆1 → q₇1 обнуляем его с конца

q₇1 → q₇R

q₇0 → q₈L

q₈1 → q₉0

q₉0 → q₈L

q₈0 → q₁₀R

q₁₀0 → q₁₀1 конец случая Х=0, Y-любое

q₁₀1 → q₅₆1 переход прибавлению 1

q₅1 → q₁₁1 -----если Х!=0, то

q₁₁1 → q₁₁R идем на первую 1 Y’а

q₁₁0 → q₁₂R

q₁₂1 → q₁₂R уменьшаем

q₁₂0 → q₁₃L массив единиц Y на 1

q₁₃1 → q₁₄0

q₁₄0 → q₁₅L

q₁₅1 → q₁₅L встали на начало Y

q₁₅0 → q₁₆R проверяем был ли Y= 0

q₁₆0 → q₁₇0 -----если Y=0, то

q₁₇0 → q₁₇L

q₁₇1 → q₁₈1 встали на последнюю 1 X’а

q₁₈1 → q₁₉0 обнуляем его с конца

q₁₉0 → q₁₈L

q₁₈0 → q₂₀R

q₂₀0 → q₂₀1 конец случая Х!=0, Y=0

q₂₀1 → q₅₆1 переход прибавлению 1

q₁₆1 → q₂₁1 -----если Y!=0, то

q₂₁1 → q₂₁R идем в конец Y

q₂₁0 → q₂₂L

q₂₂1 → q₂₂0 стираем 1

q₂₂0 → q₂₃L есть ли еще единицы?

q₂₃1 → q₂₄1 --если остались, то

q₂₄1 → q₂₄L идем на последний массив

q₂₄0 → q₂₅0 Х’ов (в процессе

q₂₅0 → q₂₆L умножения их появится >1)

q₂₆1 → q₂₆L

q₂₆0 → q₂₇L

q₂₇1 → q₂₆1

q₂₇0 → q₂₈R встаем на 0 перед 1’м X

q₂₈0 → q₂₉R –копируем этот Х в

q₂₉1 → q₃₀0 пространство слева от

q₃₀0 → q₃₁L этого 0

q₃₁0 → q₃₂1

q₃₂1 → q₃₂L

q₃₂0 → q₃₃L

q₃₃1 → q₃₃L

q₃₃0 → q₃₄1

q₃₄1 → q₃₄R

q₃₄0 → q₃₅R

q₃₅1 → q₃₅R

q₃₅0 → q₂₈0

q₂₉0 → q₃₆R

q₃₆0 → q₃₇L -корректируем результат

q₃₇0 → q₃₈1 (ликвидация лишнего 0)

q₃₈1 → q₃₈L

q₃₈0 → q₃₉R

q₃₉1 → q₄₀0

q₄₀0 → q₄₁L

q₄₁0 → q₄₂1

q₄₂1 → q₄₂L

q₄₂0 → q₄₃R

q₄₃1 → q₄₄0

q₄₄0 → q₄₅R

q₄₅1 → q₄₅R -конец коррекции и копир-я

q₄₅0 → q₄₆R идем на первую 1 Y’а

q₄₆1 → q₄₆R

q₄₆0 → q₄₇R

q₄₇1 → q₄₆1

q₄₇0 → q₄₈L

q₄₈0 → q₄₉L

q₄₉1 → q₄₉L

q₄₉0 → q₂₁R головка снова на первой единице Y’а, зацикливаем процесс умножения

q₂₃0 → q₅₀0 --в Y’e не осталось больше единиц, тогда

q₅₀0 → q₅₀L умножение закончено

q₅₀1 → q₅₁0 сдвигаем массивы единиц Х’ов в единое целое

q₅₁0 → q₅₁L (ликвидируем 0 между ними)

q₅₁1 → q₅₂1

q₅₂1 → q₅₂L

q₅₂0 → q₅₃1

q₅₃1 → q₅₄L

q₅₄1 → q₅₅1

q₅₅1 → q₅₅R

q₅₅0 → q₅₀0 цикл идет пока между Х’ми есть хоть один 0

q₅₄0 → q₅₆1 переход прибавлению 1

q₅₆1 → q₅₆L -----прибавление 1

q₅₆0 → q₅₇1

q₅₇1 → q₀1 ---------------Конец работы программы------------

 

(XY+1)+1
…..			…..			…..
	Q0

 

 

Задание №1

Из данной совокупности секвенций выбрать доказуемые, построить их доказательства, для недоказуемых показать их недоказуемость с помощью:

d) Алгоритма Квайна

e) Алгоритма редукции

f) Метода резолюций

Среди этих доказательств недоказуемости выбрать оптимальный в каждом конкретном случае.

5. X,ØU,ØXÚY X®Y.

6. XÚUÚØZ,ØXÚZ, ØUÚY X®Y.Ú

7. Ø(XÙØX).

8. ((X®Y)®Z)® YÚXÚZ.

Решение:

1. X,ØU,ØXÚY X®Y; Данная секвенция доказуема! (по таблицам истинности).

X X; _{12 12} Y Y;

X,ØU,ØXÚY X; X,ØU,ØXÚY ØY; ₁

₁₂ ØXÚY ØXÚY;X,ØU,ØXÚY XÙØY);

₁₀ X,ØU,ØXÚY ØXÚY; X,ØU,ØXÚY Ø(ØXÚY);

₉ X,ØU,ØXÚY ;

₇ X,ØU,ØXÚY Y;

X,ØU,ØXÚY X®Y;

Следовательно, данная секвенция доказуема!

2. XÚUÚØZ,ØXÚZ, ØUÚY X®Y.

Данная секвенция недоказуема! (по таблице истинности)

Метод Квайна: XÚUÚØZ,ØXÚZ, ØUÚY X®Y

Пусть X=0, тогда: Пусть X=1, тогда:

(0ÚUÚØZ)Ù(1ÚZ)Ù(ØUÚY) 1; 1ÙZÙ(ØUÚY) Y;

(UÚØZ)Ù1Ù(ØUÚY) 1; Пусть Y=0, тогда:

1ÙZÙØU 0;

Пусть Y=0, тогда: Пусть Y=1, тогда: Пусть Z=0, тогда: Пусть Z=1, тогда:

(UÚØZ)Ù1ÙØU 1; (UÚØZ)Ù1Ù1 1; 0 0; 1Ù1ÙØU 0;

Пусть Z=0, тогда: Пусть Z=1, тогда: Пусть U=0, тогда: Пусть U=0, тогда:

1Ù1ÙØU 1; UÙ1Ù1 1; 0 0; 1Ù1Ù1 0;

Пусть U=0, тогда: Пусть U=1, тогда: 1 0;

1 1; 1 1; тождественно ложно

Следовательно, данная секвенция недоказуема.

Метод редукции: XÚUÚØZ,ØXÚZ, ØUÚY X®Y;

XÚUÚØZ,ØXÚZ, ØUÚY®X®Y

Предположим противное, т.е

Докажем что при X®Y=0, (X ÚUÚØZ)Ù(ØXÚZ)Ù(ØUÚY)=1;

Чтобы выполнялось X®Y=0 надо, чтобы выполнялось:

X= 1, Y = 0.

Тогда:

(1ÚUÚØZ)Ù(0ÚZ)Ù(ØUÚ0)=1ÙZÙØU =ZÙØU=1.

Следовательно, Z=1, U=0. Значит при X= 1, Y = 0, Z=1, U=0 наше предположение истинно, следовательно, данная секвенция недоказуема!

Метод резолюций: XÚUÚØZ,ØXÚZ, ØUÚYX®Y.

Докажем противоречивость:

XÚUÚØZ, ØXÚZ, ØUÚY, Ø(X®Y)

Приведем формулы XÚUÚØZ, ØXÚZ, ØUÚY, Ø(X®Y) к КНФ.

XÚUÚØZ, ØXÚZ, ØUÚY, XÙØY.

XÚUÚØZ, ØXÚZ, ØUÚY, X, ØY.

(1) XÚUÚØZ;

(2) ØXÚZ;

(3) ØUÚY;

(4) X;

(5) ØY;

(6) res_X,Z((1),(2)) =U;

(7) res_Y((3),(5)) = ØU;

(8) res_U((6),(7)) = 0.

Противоречивость истинна, следовательно, данная секвенция недоказуема.

3. Ø(XÙØX).

Данная секвенция доказуема! (по таблице истинности)

₂ XÙØXXÙØX;XÙØXXÙØX; ₃

₁₀ XÙØXX; XÙØXØX;

₉ XÙØX;

Ø(XÙØX)

Следовательно, данная секвенция доказуема!

4. ((X®Y)®Z)®XYÚXÚZ.

Данная секвенция недоказуема! (по таблице истинности)

Метод Квайна: ((X®Y)®Z)®XYÚXÚZ.

Пусть X=0, тогда: Пусть X=1, тогда:

ØZYÚZ; 11;

Пусть Y=0, тогда: Пусть Y=1, тогда: далее док-во не требуется.

ØZZ; ØZ1;

Пусть Z=0, тогда: Пусть Z=1, тогда:

10; 01;

тождественно ложно.

Метод редукции: ((X®Y)®Z)®XYÚXÚZ.

((X®Y)®Z)®XYÚXÚZ.

Предположим противное,

Докажем что при YÚXÚZ = 0, ((X®Y)®Z)®X =1;

Чтобы выполнялось YÚXÚZ = 0, надо, чтобы X=0, Y=0, Z=0.

Тогда при X=0, Y=0, Z=0 выражение ((X®Y)®Z)®X =1 тождественно истинно, т.к 11.

Значит при X=0, Y=0, Z=0 данная секвенция недоказуема!

Метод резолюций: ((X®Y)®Z)®XYÚXÚZ.

Приведем формулу ((X®Y)®Z)®X, Ø(YÚXÚZ) к КНФ

((X®Y)®Z)®X, ØYÙØXÙØZ;

XÚØZ, ØY, ØX, ØZ.

(1) XÚØZ;

(2) ØY;

(3) ØX;

(4) ØZ;

(5) res_X((1),(2)) = ØZ;

Множество формул непротиворечиво, следовательно, данная секвенция недоказуема.

 

Задание №2

Найти формулу исчисления предикатов, истинную на алгебраической системе A и ложную на B.

A = <Q; + >, B = <N; +>.

Решение:

A: " x $ y $ z ((x+y=z)Ù(x+z=x));

B: " x $ y $ z ((x+y=z)Ù(x+z=x));

 

x+z=x означает, что z=0; значит, x+y в сумме должны давать 0. Но если взять положительный x (x>0) то, чтобы получился 0, y должен быть меньше 0, но y<0 Ï N.

 

Задание №3

Построить доказательство формулы в исчислении предикатов.

 

"x P(x)«Ø$xØP(x)

 

Решение:

 

₁₂ "xP(x)"xP(x)

₁₀ "xP(x),$xØP(x)"xP(x) Ø$xØP(x),$ xØP(x)

₉ "xP(x),$xØP(x) Ø$xØP(x),Ø"xP(x) ₉

₇ "xP(x)Ø$xØP(x)Ø$xØP(x)"xP(x) ₇

₁ "xP(x)®Ø$xØP(x); Ø$xØP(x)®"xP(x);

(("xP(x)®Ø$xØP(x))Ù(Ø$xØP(x)®"xP(x)));

"x P(x)«Ø$xØP(x)

 

 

Задание №4

Установить, выполнима ли следующая формула и если выполнима, то построить модель этой формулы.

"x$y$z$u (P(x,y)ÙP(x,z)ÙP(x,u)ÙR(y,z,u)) Ù "x ØR(x,x,x).

Решение:

1. Вынесем поочередно кванторы во внешнюю часть:

"x$y$z$u (P(x,y)ÙP(x,z)ÙP(x,u)ÙR(y,z,u)) Ù "x ØR(x,x,x) º

"x$y$z$u"v P(x,y)ÙP(x,z)ÙP(x,u)ÙR(y,z,u) Ù ØR(v,v,v) - ПНФ

 

2. Получили ПНФ. Приведем к КлНФ.

y = f(x); z = g(x); u = h(x);

P(x,f(x)), P(x,g(x)), P(x,h(x)), R(f(x),g(x),h(x)), ØR(v,v,v) – КлНФ.

 

3. Методом резолюций проверим выполнимость данной формулы:

(7) P(x,f(x));

(8) P(x,g(x));

(9) P(x,h(x));

(10) R(f(x),g(x),h(x));

(11) ØR(v,v,v);

Невозможно сделать резолютивный вывод из данного множества формул, следовательно существует

модель.

Строим модель:

A = {a, b};

0 = R(a,a,a) = ложно =R(b,b,b).

f(a) = b; g(a) = a; h(a) = a;

f(b) = a; g(b) = b; h(b) = b;

Полагаем, что:

P(a,b) = P(b,a) = истинно;

P(a,a) = P(b,b) = истинно;

R(b,a,a) = истинно = R(a,b,b).

Задание №5

Привести к пренексной и клазуальной нормальным формам следующую формулу:

Ø$x ("y P(x,y) Ú $y Q(x,y) Ú "x ($y P(x,y)®"y Q(x,y))).

Решение:

1. Удаляем отрицание:

"x (Ø"y P(x,y) Ù Ø$y Q(x,y) Ù Ø"x ($y P(x,y)®"y Q(x,y)));

2. Удаляем импликацию:

"x (Ø"y P(x,y) Ù Ø$y Q(x,y) Ù Ø"x (Ø$y P(x,y)Ú "y Q(x,y)));

3. Вносим отрицание к атомарным формулам:

"x ($y ØP(x,y) Ù "y ØQ(x,y) Ù $x ($y P(x,y)Ù $y ØQ(x,y)));

4. Выносим кванторы во внешнюю часть:

"x$y"z$u$v$w (ØP(x,y) Ù ØQ(x,z) Ù P(u,v) Ù ØQ(u,w));

5. Вынеся кванторы во внешнюю часть, получаем соответственно ПНФ и КлНФ:

"x$y"z$u$v$w (ØP(x,y) Ù ØQ(x,z) Ù P(u,v) Ù ØQ(u,w)) – КлНФ и ПНФ.

Задание №6

Методом резолюций проверить, противоречиво ли множество предложений {j₁, j₂, j₃}. Если множество непротиворечиво, то построить модель множества.

j₁= $x"y"z ØP₁(x,y,z);

j₂= "x"y$z (P₂(x) Ù P₁(x,y,z) Ù (ØP₂(y)®P₁(y,x,z)));

j₃= "x$y"z$u (P₁(x,y,z) Ù ØP₁(x,y,u)); Решение:

j₁= $x"y"z ØP₁(x,y,z);

j₂= "x"y$z (P₂(x) Ù P₁(x,y,z) Ù (ØP₂(y)®P₁(y,x,z))) º

"x"y$z (P₂(x) Ù P₁(x,y,z) Ù (P₂(y)Ú P₁(y,x,z)))

j₃= "x$y"z$u (P₁(x,y,z) Ù ØP₁(x,y,u));

 

{j₁, j₂, j₃} = {ØP₁(x,y,z), P₂(x), P₁(x,y,z), P₂(y)Ú P₁(y,x,z), P₁(x,y,z), ØP₁(x,y,u)};

 

Пусть в j₁ x=c₁; в j₂ z=c₂; в j₃ y=c₃, u=c_4, тогда:

{j₁, j₂, j₃} = {ØP₁(c₁,y,z), P₂(x), P₁(x,y,c₂), P₂(y)Ú P₁(y,x,c₂), P₁(x, c₃,z), ØP₁(x,c₃, c₄)};

(1) ØP₁(c₁,y,z);

(2) P₂(x);

(3) P₁(x,y,c₂);

(4) P₂(y)Ú P₁(y,x,c₂);

(5) P₁(x,c₃,z);

(6) ØP₁(x,c₃,c₄);

(7) res((3)(6)) = 0;

Данное множество {j₁, j₂, j₃} противоречиво! Модели не существует!

 

Задание №7

Доказать примитивную рекурсивность функций, выражая их через простейшие с помощью операторов

суперпозиции и примитивной рекурсии.

 

f(x) = 2x+1;

Доказательство ПРФ:

 

I₁¹(x)= 2*0+1= 1;

 

S (I₃³(x,y,z)) = f(x+1)= (x+1)+(x+1)+1= 2x+3;

 

 

Задание №8

Построить машины Тьюринга для вычисления функций.

f(x)= 2x+1;

Решение:

…

_q1

q₁01^x00… ® q₀01^2x+10…

Построение машины Тьюринга для вычисления функции f(x)= 2x+1:

0q₁ ® Rq₂;

1q₂ ® Rq₂;

0q₂ ® Rq₃;

0q₃ ® 1q₄;

1q₃ ® Rq₃;

1q₄ ® Lq₄;

0q₄ ® 1q₅;

1q₅ ® Lq₆;

1q₆ ® 0q₆;

0q₆ ® Lq₇;

1q₇ ® 1q₂;

0q₇ ® Rq₈;

0q₈ ® 1q₉;

1q₉ ® Lq₀;

1 Из данной совокупности секвенций выбрать доказуемые, построить их доказательства, для недоказуемых показать их недоказуемость с помощью: а) алгоритма Квайна; б) алгоритма редукции; в) метода резолюций. Среди этих доказательств недоказуемости выбрать оптимальное в каждом конкретном случае.

 

а) (y ۸ z)⊦ y ۷ z

Промежуточная секвенция: ⊦ φ ۷ φ

 

φ ⊦ φ (φ ۷ φ) ⊦ (φ ۷ φ)

5,12

(φ ۷ φ), φ ⊦ φ ۷ φ; (φ ۷ φ), φ ⊦ (φ ۷ φ)

(φ ۷ φ), φ ⊦

(φ ۷ φ) ⊦ φ ۷ φ; (φ ۷ φ) ⊦ (φ ۷ φ)

(φ ۷ φ) ⊦

⊦ φ ۷ y

 

 

Доказательство правила вывода Γ, φ ۸ ψ ⊦ χ

Γ, φ, ψ ⊦ χ

 

7,12

12, 12, 3

ψ ⊦ ψ Γ, φ, χ ⊦ χ

Γ, φ ۸ ψ, φ ⊦ ψ; Γ, φ ۸ ψ, φ ⊦ ψ  x

12, 4

По доказанному

12, 2

φ ⊦ φ Γ, φ ۸ ψ, φ ⊦ χ

Γ, φ ۸ ψ ⊦ φ Γ, φ ۸ ψ ⊦ φ  x

Γ, φ ۸ ψ ⊦ χ

 

 

y ۸ z ⊦ y ۸ z (y ۸ z) ⊦ (y ۸ z)

(y ۸ z), y ۸ z ⊦ y ۸ z; (y ۸ z), y ۸ z ⊦ (y ۸ z)

9, 12

(y ۸ z), y ۸ z ⊦

12, 12, 4

z ⊦ z (y ۸ z), y ۸ z ⊦ y ۷ z ⊦ z ۷ z

(y ۸ z), y, z ⊦ y ۷ z; (y ۸ z), y, z ⊦ y ۷ z; (y ۸ z) ⊦ z ۷ z

(y ۸ z), y ⊦ y ۷ z y ⊦ y ⊦ y ۷ y

(y ۸ z), y ⊦ y ۷ z (y ۸ z), y ⊦ y ۷ z (y ۸ z) ⊦ y ۷ y

(y ۸ z)⊦ y ۷ z

 

б) x ۷ y, x ۷ z, x ۷ z ۷ u ⊦ u ۷ y

Секвенция недоказуема.

 

· Алгоритм Квайна.

(x ۷ y) ۸ (x ۷ z) ۸ (x ۷ z ۷ u) ⊦ (u ۷ y)

 

Пусть x = 1

(1 ۷ y) ۸ (1 ۷ z) ۸ (1 ۷ z ۷ u) ⊦ (u ۷ y)

1 ۸ 1 ۸ 1 ⊦ (u ۷ y)

1 ⊦ (u ۷ y)

 

Пусть u = 0

1 ⊦ y

 

Пусть y = 0

1 ⊦ 0  противоречие. Секвенция недоказуема.

 

· Алгоритм редукций.

 

(x ۷ y) ۸ (x ۷ z) ۸ (x ۷ z ۷ u) = 1

(u ۷ y) = 0  верно, при u = 0 и y = 0

 

(x ۷ 0) ۸ (x ۷ z) ۸ (x ۷ z ۷ 0) = 1

 

x ۸ (x ۷ z) ۸ (x ۷ z) = 1

 

При x = 1:

 

1 ۸ (1 ۷ z) ۸ (1 ۷ z) = 1 z – любое

 

z – любое  1 = 1

 

При x = 1, y = 0, u = 0 секвенция недоказуема.

 

Метод резолюций.

 

1. x ۷ y

2. x ۷ z

3. x ۷ z ۷ u

4. u

5. y

6. res_z(2, 3) = x ۷ u

7. res_u(6, 4) = x

8. res_y(2, 7) = x

 Секвенция недоказуема.

в) ⊦ (y ۸ z)  (y ۷ z)

y ۸ z ⊦ y ۸ z

y ۸ z ⊦ y

y ۸ z ⊦ y ۷ z

⊦ (y ۸ z)  (y ۷ z)

 

г) x ⊦ z  x

 

x ⊦ x

x, z ⊦ x

x ⊦ z  x

2 Найти формулу исчисления предикатов истинную на алгебраической системе __ и ложную на системе __.

 

__ = < N, ≤ > __ = <N, P(x, y)>, где P(x, y) означает, что y делится на x.

 

Решение:

x P(x, x): на ___: x ≤ x - верно всегда

на ___: P(x, x) – неверно при x = 0  (0, 0) P

 

3 Построить доказательство формулы исчисления предикатов

⊦  x (P(x)  Q(x)) ۷ (x P(x) ۸ x Q(x))

Докажем: ⊦ φ ۷ φ

 

φ ⊦ φ (φ ۷ φ) ⊦ (φ ۷ φ)

5,12

(φ ۷ φ), φ ⊦ φ ۷ φ; (φ ۷ φ), φ ⊦ (φ ۷ φ)

(φ ۷ φ), φ ⊦

(φ ۷ φ) ⊦ φ ۷ φ; (φ ۷ φ) ⊦ (φ ۷ φ)

(φ ۷ φ) ⊦

⊦ φ ۷ y

 

 

P ⊦ P; P ⊦ P Q ⊦ Q; Q ⊦ Q

7, 9

P, P ⊦ P; P, P ⊦ P Q, Q ⊦ Q; Q, Q ⊦ Q

P, P ⊦ Q, Q ⊦

P ۷ Q, P, Q, P ⊦; P ۷ Q, P, Q, Q ⊦; P ۷ Q⊦P ۷ Q

P ۷ Q, P, Q, ⊦

P(x) ۷ Q(x) ⊦ (P(x)  Q(x))

P(x) ۷ Q(x) ⊦  x (P(x)  Q(x))

P(x) ۷ Q(x) ⊦ x (P(x)  Q(x)) ۷ (x P(x) ۸ x Q(x))

 

12, 4

12, 4

P ⊦ P; (P ۷ Q) ⊦ (P ۷ Q) Q ⊦ Q; (P ۷ Q) ⊦ (P ۷ Q)

(P ۷ Q),P⊦P ۷ Q;(P۷Q),P⊦(P۷Q) (P۷Q),Q⊦P۷Q; (P۷Q),Q⊦(P۷Q)

(P ۷ Q), P ⊦ (P ۷ Q), Q ⊦

(P ۷ Q) ⊦ P (P ۷ Q) ⊦ Q

(P(x) ۷ Q(x)) ⊦ x P(x) (P(x) ۷ Q(x)) ⊦ x Q(x)

(P(x) ۷ Q(x)) ⊦ x P(x) ۸ x Q(x)

(P(x) ۷ Q(x)) ⊦ x (P(x)  Q(x)) ۷ (x P(x) ۸ x Q(x))

 

По доказанному

⊦(P(x) ۷Q(x))۷ (P(x) ۷Q(x))

 

P(x)۷Q(x)⊦x(P(x)Q(x))۷(xP(x)۸xQ(x));(P(x)۷Q(x))⊦x(P(x)Q(x))۷(xP(x)۸xQ(x));

⊦(P(x) ۷Q(x))۷ (P(x) ۷Q(x))

⊦  x (P(x)  Q(x)) ۷ (x P(x) ۸ x Q(x))

 

 

4 Установить, выполнима ли следующая формула и если выполнима, то построить модель этой формулы.

 

 x  y ((x = y) ۸ P(x, y) ۸  z R(x, y, z) ۸  u R(x, y, u))

 

ß P

Модель:

 

m = <{a, b}{(a, b)}{(a, b, a)}>

ß R

 

 

5 Привести к пренексной и клазуальной нормальным формам следующую формулу.

 

x ( y P(x, y) y Q(x, y)) ۸  x (y P(x, y)  y Q(y, y)) 

x ( y P(x, y) ۷ y Q(x, y)) ۸  x (y P(x, y) ۷  y Q(y, y)) 

x ( y P(x, y) ۷ y Q(x, y)) ۸  x (y P(x, y) ۷  y Q(y, y)) 

x ( y P(x, y) ۷ y Q(x, y)) ۸  x (y P(x, y) ۸  y Q(y, y)) 

x  y  y₁ (P(x, y) ۷ Q(x, y₁)) ۸  x y (P(x, y) ۸  y Q(y, y)) 

x  y  y₁  x₁  y₂  y₃ ((P(x, y) ۷ Q(x, y₁)) ۸ P(x₁, y₂) ۸ Q(y₃, y₃)) 

КлНФ

x  y  y₁  x₁  y₂  y₃((P(x, y) ۸ P(x₁, y₂) ۸ Q(y₃, y₃)) ۷ (Q(x, y₁) ۸ P(x₁, y₂) ۸ Q(y₃, y₃))) ПНФ

 

 

6 Методом резолюций проверить противоречиво ли множество предложений {Ф₁, Ф₂, Ф₃}. Если множество непротиворечиво, то построить модель этого множества.

 

Ф₁ = x (P₁(x) ۷ (P₂(x) ۸ P₃(x)))

Ф₂ =  y x (P₄(x, y) ۸ (P₄(y, x)  (P₁(x) ۷ P₂(x))))

Ф₃ = x (P₃(x)   y P₄(x, y))

 

Ф₁ = x (P₁(x) ۷ P₂(x) ۷ P₃(x)))

Ф₂ =  y x (P₄(x, y) ۸ (P₄(y, x) ۷ P₁(x)) ۸ (P₄(y, x) ۷ P₂(x)))

Ф₃ = x y (P₃(x) ۷ P₄(x, y))

 

1. P₁(x) ۷ P₂(x) ۷ P₃(x)

2. P₄(x, c)

3. P₄(c, x) ۷ P₁(x)

4. P₄(c, x) ۷ P₂(x)

5. P₃(x) ۷ P₄(x, y)

6. res(1, 3) = P₂(x) ۷ P₃(x) ۷ P₄(c, x)

7. res(1, 4) = P₁(x) ۷ P₃(x) ۷ P₄(c, x)

8.

{c/x}

res(2, 3) = P₁(c)

9.

ß Æ

res(2, 4) = P₂(c)

10.

{c/y}

res(2, 5) = P₃(x)

 

11. res(1, 8) = res(2, 6) = P₂(c) ۷ P₃(c)

12.

{c/x}

res(1, 9) = P₁(x) ۷ P₃(x)

 

 существует модель