у = -3х2+5х-4 в точке х0= -1 равен:
а) -3; б) 5; в) -4; г) 11.
105. Если закон прямолинейного движения материальной точки задан функцией S(t)= t2+2t+3, то скорость движения через 3 секунды после начала движения будет равна:
а) 3; б) 5; в) 4; г) 8.
106. Если скорость прямолинейного движения материальной точки задана функцией V(t)= t3+2t+3, то ускорение движения через 2 секунды после начала движения будет равно:
а) 13; б) 15; в) 14; г) 8.
107. Добавьте недостающий арифметический знак (u… v)’ = u’ … v’
а) +, б) –, в) умножить, г) разделить, д) ±.
108.. Дополните формулу: 
а) u, б) v, в) u2, г) v2.
109. Дополните формулу: С’ = ….
а) 0, б) 1, в) Сх, г) С.
110. Дополните формулу: 
а) 0, б) n-1, в) n, г) n+1.
111. Дополните формулу: (5x)’= …….:
а) x 5x+1. б) 5x , в) 5x ln 5, г) ln 5.
112. Дополните формулу: cos 2x=……:
а) – 2 sin 2x, б) 2 sin 2x, в) – sin 2x, г) – 2sin x.
113. Производная функции – это…….
а) скорость процесса, описанного функцией, б) ускорение процесса, описанного функцией, в) время процесса, описанного функцией, г) значение функции при определенном значении ее аргумента.
114. Дополните формулу (u ∙ v)’ = u’∙v … u ∙ v’
а) +, б) –, в) умножить, г) разделить, д) ±.
115. Найдите скорость химической реакции, процесс которой описан формулой f(t)=t3+ t2+5:
а) 3t2+2t; б) t2+t; в) 4t4+3t3+5t; г) 
.
116. Дополните формулу 
а) cos x, б) –cos x, в) tg x, г) –sin x
117. Дополните формулу (2x3 )’= ………:
а) 2x2, б) 6x2, в) 12х, г) х4
118. Дополните формулу (sin x)’ = ……….:
а) – cos x, б) cos x,, в) tg x, г) ln x
119. Дополните формулу (x-5)’=…………..:
а) 5 x-4, б) - 5 x-4, в) -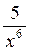 
, г) - 
120. Дополните формулу (tgx)’=…………:
а) 
, б) cos2 x,, в) ctg x, г) –tgx.
121. Дополните формулу (ctgx)’=…………:
а) 
, б) sin2 x,, в) -ctg x, г) tgx.
122. Наименьшее значение функции у = 2х+3 на отрезке [-1;2] равно:
а) 5; б) 1; в) 7; г) 11.
124. Наименьшее значение функции у = -2х+3 на отрезке [-1;2] равно:
а) 5; б) 1; в) 7; г) -1.
125. Наибольшее значение функции у = 2х+3 на отрезке [-1;2] равно:
а) 5; б) 1; в) 7; г) 11.
126. Наибольшее значение функции у = -2х+3 на отрезке [-1;2] равно:
а) 5; б) 1; в) 7; г) 11.
127. Впервые применил дифференциальное и интегральное исчисление для вычисления площадей и объемов:
а) Лейбниц, б) Фурье, в) Кеплер, г) Эйлер.
128. Обозначение неопределенного интеграла было введено:
а) Паскалем. б) Лейбницем, в) Лопиталем, г) Фурье.
129. Если известна формула, описывающая скорость перемещения какого-либо тела, то вычисление интеграла от этой функции позволяет найти:
а) функцию, описывающую перемещение тела в любой момент времени,
б) ускорение движения этого тела, в) массу этого тела, г) скорость движения в данный момент времени.
130. Множество всех первообразных для функции f(x)=-x3 имеет вид:
а) -3x2 , б) - 
в) - 
г) -3x2 +С.
131. Множество всех первообразных для функции f(x)=х+2 имеет вид:
а) 2x, б) 
, в) 
г)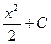 
132. Интеграл 
равен:
а) ln x +C, б) x + C, в) ex+C, г) x.
133. Интеграл 
равен:
а) x2 +x +C б) x+C в)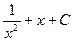 
г) 
.
134. Интеграл 
равен:
а) – cos x+c, б) ctgx+c,, в) tg x+c, г) sinx+c/
134. Интеграл 
равен:
а) – cos x+c, б) ctgx+c,, в) tg x+c, г) -sinx+c/
135. В формуле множества всех первообразных F(x) + C, С – это:
а) первообразная, б) интеграл, в) подинтегральное выражение,
г) константа интегрирования.
136. Множество всех первообразных для функции f(x)=2-x4
имеет вид:
а) 3x3 , б) 4x4 +С, в) 
, г) 
137. Множество всех первообразных для функции f(x)= -2 cos x имеет вид:
а) -2 sin x+С, б) 2 sin x+С, в) - 
sin x+С, г) sin x+С.
138. Интеграл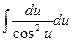 
равен:
а) 
, б) tg u + C, в) 
, г) – sin u +C.
139. Определенный интеграл функции f(x) на отрезке [ а,в ] численно равен:
а) площади криволинейной трапеции, ограниченной графиком этой функции, осью ОХ и прямыми х=а и х=в; б) длине отрезка [а,в]; в) длине дуги кривой
у=f(x) на отрезке [ а,в ]; г) периметру криволинейной трапеции, ограниченной графиком этой функции, осью ОХ и прямыми х=а и х=в.
140. Определенный интеграл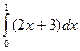 
равен:
а) 13; б) 5; в) 10; г) 8.
141. Определенный интеграл 
равен:
а) 0; б) 5; в) 2; г) 8.
142. Формула n(A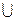 
B) =n(A)+n(B) задает в комбинаторике правило:
а) объединения; б) правило суммы; в) правило пересечения;
г) правило умножения.
143. Формула n(A 
B) =n(A)* n(B) задает в комбинаторике правило:
а) объединения; б) правило суммы; в) правило пересечения;
г) правило умножения.
144. Число Ank всевозможных размещений без повторений из n по к элементов вычисляется по формуле:
а) 
; б) 
; в) 
; г) 
145. Число Рк всевозможных перестановок без повторений из к элементов вычисляется по формуле:
а) 
; б) 
; в) 
; г) 
.
146. Число Сnk всевозможных сочетаний без повторений из n по к элементов вычисляется по формуле:
а) 
; б) 
; в) 
; г) 
147. Дано множество А={a,b,c}. Число всевозможных размещений с повторениями из трех по два элемента равно:
а) 8; б) 6; в) 10; г) 9.
148. Дано множество А={a,b,c}. Число всевозможных размещений без повторений из трех по два элемента равно:
а) 8; б) 6; в) 3; г) 9.
149. Дано множество А={a,b,c,е}. Число всевозможных перестановок без повторений из четырех элементов равно:
а) 8; б) 24; в) 10; г) 9.
150. Дано множество А={a,b,c,е}. Число всевозможных сочетаний без повторений из четырех по два элемента равно:
а) 8; б) 6; в) 10; г) 12.
151. На первой полке стоит 5 книг, на второй – 10. Число всевозможных способов выбора одной книги с первой полки и одной книги со второй полки равно:
а) 15; б) 5; в) 50; г) 25.
152. Ученик должен выполнить практическую работу по математике. Ему предложили на выбор 17 тем по алгебре и 13 тем по геометрии. Число способов выбора одной темы дл практической работы равно:
а) 17; б) 13; в) 30; г) 221.
153. Медсестра должна сделать уколы шести больным. Учитывая различную последовательность инъекций, число всевозможных способов равно:
а) 6; б) 36; в) 720; г) 120.
154. Событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий, называется:
а) вероятным, б) достоверным, в) возможным, г) случайным.
155. Событие, которое при осуществлении совокупности условий может либо произойти, либо не произойти, называется:
а) вероятным, б) достоверным, в) возможным, г) случайным.
156. Укажите число равновозможных событий в эксперименте «бросание монеты»:
а) 1, б) 2, в) 3, г) 4.
157. Число равновозможных событий в эксперименте «выстрел по цели» равно:
а) 1, б) 2, в) 3, г) 4.
158. Число равновозможных событий в эксперименте «извлечение карты определенного цвета» равно:
а) 2, б) 4, в) 6, г) 12.
159. Суммой (объединением) двух событий А и В называется третье событие С, заключающееся в том, что произойдет:
а) хотя бы одно из них; б) только А, в) только В, г) оба события одновременно.
160. Полная группа событий – это:
а) все события, которые могут произойти при данном испытании с одинаковой вероятностью;
б) все события, которые могут произойти в данном испытании с различной вероятностью;
в) сумма тех событий, вероятность которых в данном испытании одинакова;
г) все события, которые могут произойти или не произойти при данном испытании.
161. События А, В, С и D образуют полную группу. Вероятности событий таковы: Р (A)= 0,2; Р (В) = 0,3; Р (С) = 0,3. Вероятность события D равна:
а) 0,1 б) 0,5 в) 0,2 г) 1
162. Назовите событие, противоположное событию А, образующему с ним полную группу, если событие А – попадание по цели:
а) попадание в десятку, б) промах, в) отказ от выстрела; г) попадание в мишень.
163. В результате технического контроля 3 детали из партии в 100 штук оказались бракованными. Относительная частота брака равна:
а) 0,01 б) 0,03 в) 0,3 г) 0,1.
164. Выберите три вида событий, изучаемых теорией вероятности:
а) вероятные; б) достоверные; в) случайные; г) невозможные
165. Событие, которое заведомо не произойдет, если будет осуществлена совокупность условий, называется:
а) вероятным, б) достоверным, в) невозможным, г) случайным.
166. Испытания, которые можно провести в уме, без физического эксперимента называются:
а) виртуальными экспериментами, б) воображаемыми экспериментами,
в) мысленными экспериментами; г) неопределенными экспериментами.
167. Число равновозможных событий в эксперименте «бросание игральной кости» равно:
а) 2, б) 3, в) 4, г) 6.
168.Число равновозможных событий в эксперименте «извлечение карты определенной масти» равно:
а) 2, б) 4, в) 6, г) 12.
169. Число равновозможных событий в эксперименте «извлечение из колоды карт короля» равно:
а) 2, б) 4, в) 6, г) 12.
170. Вероятность того, что при бросании двух монет выпадут два герба, равна:
а) 0,5; б) 0,25; в) 0,75; г) 1.
171. Вероятность появления нечетного числа очков при бросании игрального кубика равна:
а) 1; б) 0,5; в) 0,6; г) 0,2.
172. Бросают два игральных кубика. Вероятность появления 7очков равна:
а) 1/6; б) 0,5; в) 0,6; г) 0,2.
173. В ящике 4 белых и 6 черных шаров. Вероятность того, что случайным образом вынут белый шар, равна:
а) 1; б) 0,6; в) 0,4; г) 0,2.
174. В ящике 4 белых и 6 черных шаров. Вероятность того, что случайным образом вынули два белых шара, равна:
а) 1/4; б) 1/15; в) 2/15; г) 0,6.
175. В ящике 4 белых,6 черных и 10 зеленых шаров. Вероятность того, что случайным образом вынули белый или черный шар, равна:
а) 1; б) 0,5; в) 0,4; г) 0,6.
176. В ящике 4 белых,6 черных и 10 зеленых шаров. Вероятность того, что случайным образом вынули зеленый или черный шар, равна:
а) 0,75; б) 0,5; в) 0,8; г) 0,6.
178. Случайная величина называется дискретной, если она:
а) принимает только конкретные значения; в)принимает любые значения;
в) задана на ограниченном промежутке; г) задана на неограниченном промежутке.
179. Разброс случайной величины вокруг ее среднего значения это:
а) дисперсия, б) варианта, в) последовательность,
г) математическое ожидание.
180. Любое значение из выборки называется:
а) модой, б) вариантой, в) последовательностью,
г) генеральной совокупностью.
181. Центр выборки, вокруг которого группируются элементы выборки – это:
а) среднее значение, б) мода, в) медиана, г) дисперсия
182. Элемент выборки, с наиболее часто встречающимся значением, -это:
а) среднее значение, б) медиана, в) мода, г) дисперсия.
183. Медиана ряда чисел 2,4,6,8,10,12,14 равна:
а) 7; б) 8; в) 9; г) 10.
184. Медиана ряда чисел 2,4,6,8,10,12,14,16 равна:
а) 7; б) 8; в) 9; г) 10.
185. Мода совокупности элементов 3,6,9,7,3,2,6,12,3 равна:
а) 12; б) 6; в) 3; г) 2.
186. Если дисперсия равна 4, то среднеквадратическое отклонением равно:
а) 8; б) 2; в) 0,25; г) 1
187. Сумма произведений значений случайной величины на вероятность этой величины это:
а) дисперсия, б) симметрия, в) эксцесс, г) математическое ожидание
188. Относительная частота события определяется:
а) до проведения испытания в результате мысленного
эксперимента, б) после проведения испытания, по его результатам.
189. Сумма вероятностей двух событий, составляющих полную группу, равна:
а) 0, б) 0,5, в) 1, г) 2.
190. Два единственно возможных события, образующих полную группу, называются:
а) противоречивыми, б) противоположными, в) дополняющими друг друга,
г) отрицательными.
191. Понятие геометрической вероятности применяется в тех случаях, когда:
а) количество возможных исходов испытания конечно;
б) количество возможных исходов испытания бесконечно;
в) только в геометрии; г) никогда.
192. Величину, которую можно измерять, контролировать или изменять в исследованиях, называют:
а) переменной, б) константой, в) вариантой, г) инвариантой.
193. Переменные, которые варьируются исследователем, называются:
а) зависимыми, б) независимыми, в) заданными, г) определенными.
194. Группа элементов, выбранная для исследования из всей совокупности элементов, называется:
а) выборкой, б) вариантой, в) совокупностью, г) набором.
195. Любое значение из выборки называется:
а) модой, б) вариантой, в) последовательностью, г) генеральной совокупностью.
196. Если дисперсия равна 9, то среднеквадратическое отклонением равно:
а) 18, б) 81; в) 3; г) 18.
197. Величина, характеризующая разброс случайной величины вокруг ее среднего значения, это:
а) дисперсия, б) симметрия, в) эксцесс, г) среднеквадратическое отклонение.
198. Закон распределения вероятностей дискретной случайной величины Х имеет вид:
| Х | |||
| Р | 0,1 | Р2 | 0,6 |
Тогда вероятность р2 равна: а) 0,3; б) 0,7; в) 0; г) 0,5.
199. Математическое ожидание дискретной случайной величины, заданной законом распределения, равно:
| Х | |||
| Р | 0,3 | 0,1 | 0,6 |
а) 2,3; б) 2,1; в) 0,9; г) 1,5.