Цель работы
1. Изучить понятие математической модели.
2. Рассмотреть примеры задач линейного программирования.
3. Усвоить графический метод решения задач линейного программирования.
4. Научиться приведению задач линейного программирования к стандартной форме.
Теоретическое введение
Понятие математической модели. Математическая модель в задачах линейного программирования (ЛП)
Линейное программирование – это раздел высшей математики, посвященный решению задач, связанных с нахождением экстремумов функций нескольких переменных при наличии ограничений на переменные. Методами линейного программирования решаются задачи о распределении ресурсов, планировании выпуска продукции, ценообразовании, транспортные задачи и т.п.
Любое описание некоторой задачи в виде формул, алгоритмов называется математической моделью этой задачи.
Построение математической модели задачи включает следующие этапы:
1) выбор переменных задачи;
2) составление системы ограничений;
3) выбор целевой функции.
Переменными задачи называются величины х1, х2, …хn, которые полностью характеризуют экономический процесс. Их обычно записывают в виде вектора A = (х1, х2, …хn).
Система ограничений включает в себя систему уравнений и неравенств, которым удовлетворяют переменные задачи и которые следуют из ограниченности ресурсов или других экономических или физических условий.
Целевой функцией называют функцию переменных задачи, которая характеризует качество выполнения задачи, и экстремум которой требуется найти.
Общая задача математического программирования формулируется следующим образом:
найти экстремум целевой функции и соответствующие ему переменные при условии, что эти переменные удовлетворяют системе ограничений и условиям неотрицательности.
Функция (1.1) называется целевой функцией, а ограничения (1.2) – системой ограничений задачи.
Если по условию задачи требуется найти такие значения переменных, при которых целевая функция (1.1) будет иметь максимальное значение, то говорят, что целевая функция подлежит максимизации (или направлена на максимум). Если требуется, чтобы целевая функция принимала минимальное значение, то говорят, что она подлежит минимизации (направлена на минимум).
Обратите внимание на полученный результат. Целевая функция является линейной функцией переменных х1, х2, …хn; сами ограничения на значения переменных х1, х2, …хn имеют вид линейных неравенств. Все это и определило название этого класса задач – задачи линейного программирования.
В большинстве задач (но не всегда) требуется, чтобы переменные принимали неотрицательные значения (ограничение на неотрицательность); в некоторых задачах требуется, чтобы переменные принимали целочисленные значения (ограничения на целочисленность).
Линейная математическая модель может быть построена для многих задач, решаемых на практике.
Любые значения переменных, удовлетворяющие ограничениям задачи (1.2), называются допустимыми решениями (независимо от того, какое значение при этом принимает целевая функция). Большинство задач имеет бесконечно много допустимых решений. Все множество допустимых решений представляет собой область допустимых решений (ОДР).
Допустимые значения переменных, при которых целевая функция принимает максимальное или минимальное значение (в зависимости от постановки задачи), т.е. достигает экстремума, представляют собой оптимальное решение.
Методика выполнения работы
Примеры задач ЛП
Пример 1.1. Предприятие химической промышленности выпускает соляную и серную кислоту. Выпуск одной тонны соляной кислоты – 25 денежных единиц (ден. ед.)., выпуск одной тонны серной кислоты – 40 ден. ед. Для выполнения государственного заказа необходимо выпустить не менее 200 т соляной и не менее 100 т серной кислоты. Кроме того, необходимо учитывать, что выпуск кислот связан с образованием опасных отходов. При выпуске одной тонны соляной кислоты образуется 0,5 т опасных отходов, при выпуске одной тонны серной кислоты – 1,2 т опасных отходов. Общее количество опасных отходов не должно превышать 600 т, так как превышение этого ограничения приведет к выплате предприятием крупного штрафа.
Требуется определить, сколько соляной и серной кислоты должно выпустить предприятие, чтобы получить максимальную прибыль.
Составим математическую модель задачи. Для этого введем переменные. Обозначим через x1 количество выпускаемой соляной кислоты (в тоннах), через x2 – количество серной кислоты.
Составим ограничения, связанные с необходимостью выполнения государственного заказа. Предприятию необходимо выпустить не менее 200 т соляной кислоты. Это ограничение можно записать следующим образом: x1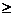 
200. Аналогично составим ограничение, устанавливающее, что предприятие должно выпустить не менее 100 т серной кислоты: x2 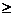100.
Составим ограничение на опасные отходы. При выпуске одной тонны соляной кислоты образуется 0,5 т опасных отходов; значит, общее количество опасных отходов при выпуске соляной кислоты составит 0,5x1 т. При выпуске серной кислоты образуется 1,2x2 т опасных отходов. Таким образом, общее количество опасных отходов составит 0,5x1+1,2x2 т. Эта величина не должна превышать 600 т. Поэтому можно записать следующее ограничение: 0,5x1+1,2x2 
600.
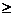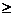Кроме того, переменные по своему физическому смыслу не могут принимать отрицательных значений, так как они обозначают количество выпускаемых кислот. Поэтому необходимо учитывать ограничения неотрицательности: x1 0; x2 0.
В данной задаче требуется определить выпуск кислот, при котором прибыль будет максимальной. Прибыль от выпуска одной тонны соляной кислоты составляет 25 ден. ед.; значит прибыль от выпуска соляной кислоты составит 25x1 ден. ед. Прибыль от выпуска серной кислоты составит 40x2 ден. ед. Таким образом, общая прибыль от выпуска кислот составит 25x1+40x2 ден. ед. Требуется найти такие значения переменных x1 и x2, при которых эта величина будет максимальной. Таким образом, целевая функция для данной задачи будет иметь следующий вид:
Е=25x1+40x2→ max.
Приведем полную математическую модель рассматриваемой задачи:
X1 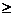200
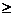x2 100
0,5x1+1,2x2 600
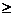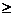x1 0; x2 0
Е=25x1+40x2→ max.
В этой задаче имеется два ограничения «больше или равно» и одно ограничение «меньше или равно». Целевая функция подлежит максимизации.
Пример 1.2. Пусть в условиях задачи 1.1 из-за ужесточения требований к экологической безопасности требуется свести к минимуму количество опасных отходов. В то же время необходимо учитывать, что для того, чтобы производство кислот было экономически целесообразным, необходимо получить прибыль не менее 20 тыс. ден. ед.
Математическая модель такой задачи имеет следующий вид:
x1 
200
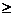x2 100
25x1+40x2 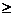20000
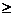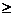x1 0; x2 0
Е= 0,5x1+1,2x2 → min.
Третье ограничение в этой модели устанавливает, что прибыль от выпуска кислот должна составлять не менее 20 тыс. ден.ед. Целевая функция представляет собой количество опасных отходов; эта величина подлежит минимизации.
Графический метод решения задач ЛП
Графический метод применяется для решения задач, в которых имеются только две переменные. Для таких задач имеется возможность графически изобразить область допустимых решений (ОДР).
Примечание. Графический метод может применяться также для решения задач с любым количеством переменных, если возможно выразить все переменные задачи через какие-либо две переменные.
Как отмечено выше, ОДР – это множество значений переменных, удовлетворяющих ограничениям (1.2). Таким образом, для задач с двумя переменными ОДР представляет собой множество точек (x1; x2), т.е. некоторую область на плоскости (обычно многоугольник). Для задач с тремя переменными ОДР представляет собой многогранник в пространстве, для задач с большим количеством переменных – некоторую область многомерного пространства. Можно доказать, что экстремум (минимум или максимум) целевой функции всегда достигается при значениях переменных, соответствующей одной из угловых точек ОДР. Другими словами, оптимальное решение всегда находится в угловой точке ОДР. Поэтому задачу линейного программирования с двумя переменными можно решить следующим образом: построить ОДР на плоскости в системе координат (x1; x2), определить все угловые точки ОДР, вычислить значения целевой функции в этих точках и выбрать оптимальное решение.
Решим графическим методом задачу из примера 1.1.
Решение показано на рис. 1.1.
Рис. 1.1 Решение примера 1.1 графическим методом
Ограничение x1 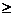200 задается вертикальной линией x1=200. Все точки (x1; x2), расположенные справа от этой линии, удовлетворяют ограничению x1 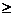200, расположенные слева – не удовлетворяют. Ограничение x2 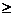100 задается горизонтальной линией x2=100. Все точки, расположенные сверху от этой линии, удовлетворяют ограничению x2 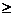100, расположенные снизу – не удовлетворяют.
Для построения линии, задающей ограничение 0,5x1+1,2x2 600, удобно записать его в виде равенства: 0,5x1+1,2x2=600. Выразим одну из переменных через другую: x2=-0,41x1+500. это уравнение прямой. Построим эту прямую. Она разбивает координатную плоскость на две полуплоскости. В одной из этих полуплоскостей находятся точки, удовлетворяющие ограничению, в другой – не удовлетворяющие. Чтобы найти полуплоскость, удовлетворяющую ограничению 0,5x1+1,2x2 600, подставим в него координаты любой точки, например, (0; 0). Для этой точки ограничение выполняется. Значит, она находится в полуплоскости, удовлетворяющей ограничению.
Пересечение всех полуплоскостей, удовлетворяющих ограничениям задачи, представляет собой ОДР. На рис. 1.1 она выделена серым цветом.
Оптимальное решение находится в одной из угловых точек ОДР (на рис. 1.1 они обозначены как А, В, С). Эти точки можно найти из построенного графика или путем решения соответствующих систем из двух уравнений. Найдем значения целевой функции в этих точках:
Е(А) = 25∙200 + 40∙100=9000;
Е(В) = 25∙200 + 40∙416,67 = 21666,8;
Е(С) = 25∙960 + 40∙100 = 28000.
Таким образом, оптимальное решение находится в точке С= (960; 100). Это означает, что предприятию следует выпустить 960 т соляной кислоты и 100 т серной кислоты. Прибыль при этом составит 28000 ден.ед. Можно также найти количество опасных отходов, которое будет получено при производстве кислот: 0,5 960 + 1,2∙100 = 600 т.
Решим графическим методом задачу из примера 1.2. Решение показано на рис. 1.2.
Рис. 1.2 Решение задачи 1.2 графическим методом
В данном случае ОДР имеет только две угловые точки (А и В). Найдем для них значение целевой функции:
Е(А)= 0,5 ∙200+1,2 ∙ 375 =550;
Е (В) = 0,5 ∙640+1,2∙100 =440.
Таким образом, оптимальное решение находится в точке В(640; 100). Это означает, что предприятию следует выпустить 640 т соляной и 100 т серной кислоты. При этом образуется 440 т опасных отходов. Можно также найти прибыль от производства кислот: 25 ∙ 640 + 40 ∙100 = 20 000 ден.ед.