Изменение длины кривой на поверхности
Пусть  (u, v), где u, v∈W –регулирующая поверхность: u=u(t), v=v(t).
(u, v), где u, v∈W –регулирующая поверхность: u=u(t), v=v(t).
Кривая в области W, тогда  (t)=
(t)=  (u(t), v(t)) –соответствующая кривая на поверхности.
(u(t), v(t)) –соответствующая кривая на поверхности.
Вопрос об измерении длины кривой на поверхности лежит в основе геометрической поверхности. Как мы знаем, для вычисления ее длины необходимо знать производные соотв. В ф.Вспомним некоторые сведения из математического анализа: пусть f(u, v), u(t), v(t) – гладкие функции, g(t)=f(u(t), v(t))  g’(t)=
g’(t)= 
Можно доказать, что дляв. Ф. она аналогичная:
 ’(t)=
’(t)=  u’(u(t), v(t))u’(t)+
u’(u(t), v(t))u’(t)+  v’(u(t), v(t))v’(t)
v’(u(t), v(t))v’(t)
|  (t)|=
(t)|= 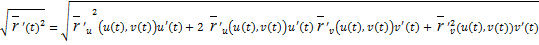
Введем обозначения(следуя Гаусу): 


E, F, G – скалярные функции переменных u и v, определенные на W. Т.о. для длины дуги кривой получаем: 
С учетом  формулу можно записать в виде:
формулу можно записать в виде:
 (1)
(1)
Дифференциальное выражение 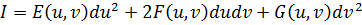 (2)
(2)
называется первой квадратичной формой поверхности(ПКФ).
Функции E(u, v), F(u, v), G(u, v) называются коэффициентами первой квадратичной формы поверхности.
Значение (2) формула (1) может быть записана очень кратко:  (3)
(3)
Пример. Найти ПКФ поверхности вращения
 (u, v)
(u, v) 

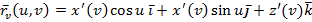

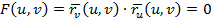


Пусть  и
и  – регулярные поверхности, имеют одну и туже ПКФ:
– регулярные поверхности, имеют одну и туже ПКФ:  ,
,  .
.
Кривая область W Þ 
 – cсоответственные кривые на поверхности r1 и r2. Из формулы (3)Þ кривые r1(t) и r2(t) имеют одинаковую длину. Т.к. Внешняя геометрическая полнота определяется измерением кривых на поверхности, то можно сделать вывод, что поверхности r1 и r2 имеют одну и туже внутреннюю геометрию, т.е. одну поверхность можно получить путем изгибания другой поверхности. Такое изгибание можно описать отображением
– cсоответственные кривые на поверхности r1 и r2. Из формулы (3)Þ кривые r1(t) и r2(t) имеют одинаковую длину. Т.к. Внешняя геометрическая полнота определяется измерением кривых на поверхности, то можно сделать вывод, что поверхности r1 и r2 имеют одну и туже внутреннюю геометрию, т.е. одну поверхность можно получить путем изгибания другой поверхности. Такое изгибание можно описать отображением 
Теорема: если 2 поверхности имеют одну и туже ПКФ, то их внутренние геометрии совпадают.
Замечание: при этом поверхности внешне будут совершенно различны.
ПКФ и внутренняя геометрия регулярной поверхности
Пусть  – регулярная кривая в пространстве, и – ее натуральный параметр.
– регулярная кривая в пространстве, и – ее натуральный параметр.
 – поверхность касательной к этой кривой. Найдем ее ПКФ: пускай
– поверхность касательной к этой кривой. Найдем ее ПКФ: пускай 
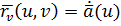
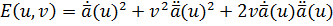


В силу теорем 3 и 4 § 2 получаем:  Þ
Þ 
 , т.к.
, т.к. 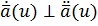
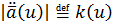 Þ
Þ  Þ
Þ 
Видим, что I зависит от кривизны, но не зависит от кручения.
Рассмотрим вспомогательную кривую  , которая имеет такую же кривизну k и нулевое кручение X(u)=0 (существование этой кривой следует из теоремы Серре). Поверхности касательных кривых
, которая имеет такую же кривизну k и нулевое кручение X(u)=0 (существование этой кривой следует из теоремы Серре). Поверхности касательных кривых  и
и  имеют одну и туже самую ПКФ Þ их внутренние геометрии совпадают, но
имеют одну и туже самую ПКФ Þ их внутренние геометрии совпадают, но  – плоская кривая. Все это обозначает, что поверхность касательной любой кривой локально имеет одну и туже внутреннюю геометрию, что и плоскость. Это так называемая теорема Эйлера.
– плоская кривая. Все это обозначает, что поверхность касательной любой кривой локально имеет одну и туже внутреннюю геометрию, что и плоскость. Это так называемая теорема Эйлера.
Внутренняя геометрия малого куска произвольной поверхности касательной совпадает с внутренней геометрией куска плоскости. Поверхности, малые куски которых изгибаются на плоскости(т.е. имеют одну и туже внутреннюю геометрию, что и плоскость) называются развертывающимися.
Если поверхности имеют одинаковые ПКФ, то у них одна и также внутренняя геометрия. Имеет ли место обратная теорема?
Теорема(критерий изгибаемости): регулярная поверхность F1изгибается на регулярной поверхности F2только тогда, когда существуют такие параметризации, что их ПКФ совпадают
Пусть F1 и F2 – 2 одинаковых куска плоскости с разными параметризациями. Пусть u=x, v=y Þ 
Пусть u=OM, v=xOMÞ 

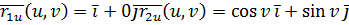

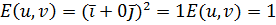



Видно, что 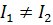 , хотя F1 и F2 одна и также поверхность.
, хотя F1 и F2 одна и также поверхность.