Случай № 1.
Пусть дана  . Рассмотрим первый случай: характеристический многочлен
. Рассмотрим первый случай: характеристический многочлен  имеет ровно n корней, среди которых нет кратных, т.е. все собственные значения матрицы А различны, т.е.
имеет ровно n корней, среди которых нет кратных, т.е. все собственные значения матрицы А различны, т.е.  , Sp A – простой. В этом случае построим базисные многочлены lk(x):
, Sp A – простой. В этом случае построим базисные многочлены lk(x):
 .
.
Пусть f(x) – функция, определенная на спектре матрицы А и значениями этой функции на спектре будут  . Надо построить
. Надо построить  .
.
Построим:
 .
.
Обратим внимание, что  .
.


Пример: Построить интерполяционный многочлен Лагранжа-Сильвестра для матрицы 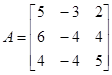 .
.
 Построим базисные многочлены:
Построим базисные многочлены:



Тогда для функции f(x), определенной на спектре матрицы А, мы получим:
 .
.
Возьмем  , тогда интерполяционный многочлен
, тогда интерполяционный многочлен
 .
.
Случай № 2.
Характеристический многочлен матрицы А имеет кратные корни, но минимальный многочлен этой матрицы является делителем характеристического многочлена и имеет только простые корни, т.е.  . В этом случае интерполяционный многочлен строится так же как и в предыдущем случае.
. В этом случае интерполяционный многочлен строится так же как и в предыдущем случае.
Случай № 3.
Рассмотрим общий случай. Пусть минимальный многочлен имеет вид:
 ,
,
где m1+m2+…+ms=m, deg r(x)<m.
Составим дробно-рациональную функцию:
 и разложим ее на простейшие дроби.
и разложим ее на простейшие дроби.

Обозначим:  . Умножим (*) на
. Умножим (*) на  и получим
и получим

где 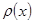 – некоторая функция, не обращающаяся в бесконечность при
– некоторая функция, не обращающаяся в бесконечность при  .
.
Если в (**) положить  , получим:
, получим:

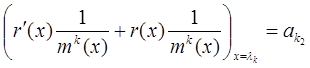
Для того, чтобы найти ak3 надо (**) продифференцировать дважды и т.д. Таким образом, коэффициент aki определяется однозначно.
После нахождения всех коэффициентов вернемся к (*), умножим на m(x) и получим интерполяционный многочлен r(x), т.е.
 .
.
Пример: Найти f(A), если 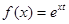 , где t – некоторый параметр,
, где t – некоторый параметр,
 .
.
Найдем минимальный многочлен матрицы А:


 .
.
Проверим, определена ли функция на спектре матрицы А



Умножим (*) на (х-3)

при х=3
 Þ
Þ 
Умножим (*) на (х-5)

 .
.
Таким образом,  - интерполяционный многочлен.
- интерполяционный многочлен.

Пример 2.
Если  , то доказать, что
, то доказать, что 
Найдем минимальный многочлен матрицы А:
 - характеристический многочлен.
- характеристический многочлен.



d2(x)=1, тогда минимальный многочлен

 .
.
Рассмотрим f(x)=sin x на спектре матрицы:
 Þ функция является определенной на спектре.
Þ функция является определенной на спектре.
Умножим (*) на 
 Þ
Þ  .
.
Умножим (*) на 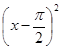 :
:

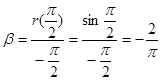 .
.
Вычислим g, взяв производную (**):
 . Полагая
. Полагая  ,
,
 , т.е.
, т.е.  .
.
Итак,  ,
,
 ,
,
 ,
,
 .
.
ЧТД.
Пример 3.
Пусть f(x) определена на спектре матрицы, минимальный многочлен которой имеет вид  . Найти интерполяционный многочлен r(x) для функции f(x).
. Найти интерполяционный многочлен r(x) для функции f(x).
Решение: По условию f(x) определена на спектре матрицы А Þ f(1), f’(1), f(2), f ‘(2), f ‘’ (2) определены.
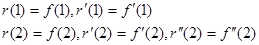 .
.
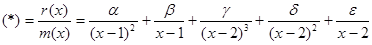

 .
.
Используем метод неопределенных коэффициентов:




Если f(x)=ln x
f(1)=0 f’(1)=1
f(2)=ln 2 f’(2)=0.5 f’’(2)=-0.25
Простые матрицы.
Пусть матрица  , так как С алгебраически замкнутое поле, то характеристический многочлен
, так как С алгебраически замкнутое поле, то характеристический многочлен  , где
, где  , ki – алгебраическая кратность корня
, ki – алгебраическая кратность корня  .
.
Обозначим множество векторов удовлетворяющих собственному значению 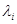
 - подпространство,
- подпространство,  , где r – ранг матрицы
, где r – ранг матрицы  .
.
Теорема. Если квадратная матрица А имеет собственное значение 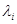 , а матрица
, а матрица  имеет
имеет  , то
, то  имеет кратность
имеет кратность  .
.
DF. Размерность  называется геометрической кратностью собственного значения
называется геометрической кратностью собственного значения  .
.
В свете этого определения теорема переформулируется следующим образом:
Теорема. Алгебраическая кратность собственного значения не меньше его геометрической кратности.
DF. Матрица  называется простой, если аглебраическая кратность каждого ее собственного значения совпадает с его геометрической кратностью.
называется простой, если аглебраическая кратность каждого ее собственного значения совпадает с его геометрической кратностью.
Из линейной алгебры следует, что матрица  простая тогда и только тогда, когда
простая тогда и только тогда, когда  .
.
Если матрица А простая, тогда существует n линейно независимых собственных векторов x1, x2, …,xn таких, что  , для
, для  . Запишем это равенство в матричном виде:
. Запишем это равенство в матричном виде:

 , т.е. А – простая тогда и только тогда, когда
, т.е. А – простая тогда и только тогда, когда  и
и  .
.
Замечание. Обратим внимание на то, что собственные значения А и А’ совпадают. Действительно, собственные значения для А’ это значения  . Таким образом характеристические многочлены матриц совпадают. Размерность
. Таким образом характеристические многочлены матриц совпадают. Размерность  , тогда
, тогда  . Поэтому, если
. Поэтому, если 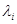 - собственное значение матрицы А, то и
- собственное значение матрицы А, то и  является собственным значением матрицы А’, т.е. существует
является собственным значением матрицы А’, т.е. существует  , что
, что  (*) или
(*) или  . Транспонируем (*) и получим
. Транспонируем (*) и получим  (транспонируем это равенство). В этом случае
(транспонируем это равенство). В этом случае 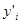 называют левым собственным вектором матрицы А. Соответственно,
называют левым собственным вектором матрицы А. Соответственно,  - называют правым собственным подпространством,
- называют правым собственным подпространством, 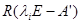 - называют левым собственным подпространством.
- называют левым собственным подпространством.
Рассмотрим следующую конструкцию: если матрица А простая, то существует n линейно независимых собственных векторов x1, x2, …, xn и существует n линейно независимых собственных векторов y1, y2,…,yn, где x1, x2, …, xn такие, что  ,
, 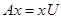 (1); y1, y2,…,yn такие, что
(1); y1, y2,…,yn такие, что  (2),
(2),  .
.
Запишем равенство (1) в виде  (3) Þ что, если А – простая, то существуют матрицы X и Y, что
(3) Þ что, если А – простая, то существуют матрицы X и Y, что  или
или  (**).
(**).
DF. Множества векторов x1, x2, …, xn и y1, y2,…,yn удовлетворяющие условию 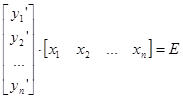 , т.е.
, т.е. 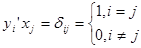 называются квазиортогональными.
называются квазиортогональными.
Учитывая равенство (**) и определение делаем вывод: множества левых и правых собственных векторов простой матрицы А квазиортогональны и  .
.
Очень важной для матриц является следующая теорема:
СПЕКТРАЛЬНАЯ ТЕОРЕМА. Если А – простая матрица порядка n над полем С и p(x) многочлен из кольца C[x], и x1, x2, …, xn и y1, y2,…,yn – множества правых и левых собственных векторов матрицы А, то  , а сопутствующая матрица
, а сопутствующая матрица  , где
, где  .
.
Следствие. Сопутствующие матрицы обладают следующими свойства:
1. 
2. 
3. 
Пример. Показать, что матрица 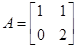 простая. Найти сопутствующие матрицы для матрицы А и использовать их для А20, p(x)=x20.
простая. Найти сопутствующие матрицы для матрицы А и использовать их для А20, p(x)=x20.
Решение:


 Þ
Þ
существуют 2 линейно независимые правые и левые системы собственных векторов.
Найдем правые собственные векторы:


Найдем левые собственные векторы:


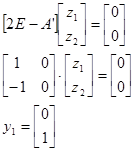
Найдем сопутствующие матрицы:


 .
.