Пересечение многогранников.

Для построения касательной плоскости к поверхности в ее точке М достаточно через эту точку провести на поверхности только две кривые линии α и b, и к ним построить касательные прямые tα и tb (рисунок 10-2).

Две эти касательные прямые и определяют касательную плоскость Е. Вполне естественно, что в качестве таких кривых линий поверхности выбирают ее графически простые линии. Например, для линейчатых поверхностей одной из этих кривых может служить ее прямолинейная образующая, (она будет совпадать со своей касательной), а для поверхности вращения – ее параллель (окружность). В зависимости от вида поверхности касательная плоскость может касаться ее в одной точке (рисунок 10-1 – сфера), по прямой линии (рисунок 10-2а – конус), по кривой линии (рисунок 10-2б – тор).

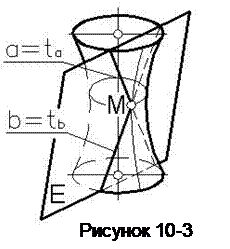В приведенных примерах поверхность располагается по одну сторону от касательной плоскости и не пересекается последней. Однако касательная плоскость может и пересекать поверхность. Так, плоскость Е, касательная к однополостному гиперболоиду, пересекает его по двум образующим α и b, которые при этом являются и касательными tα и tb, определяющими касательную плоскость Е (рисунок 10-3).

Рассмотрим примеры построения касательной плоскости к различным поверхностям.

Пример 1. Построить плоскость Е, касательную к поверхности вращения в ее точке М (рисунок 10-4).

В качестве двух кривых линий поверхности, касательные к которым определят искомую плоскость Е, выберем параллель h и меридиан α, проходящие через точку М.

Параллель h является окружностью, расположенной горизонтально, и построение касательной th к ней не составляет труда. Для построения касательной tα к меридиану α предварительно преобразуем чертеж, повернув меридиан вокруг оси поверхности вращения до фронтального положения α1. При этом точка М займет положение М1. Теперь построим касательную tα к фронтальному меридиану α1 в его точке М1 и, произведя обратное вращение, получим искомую касательную к меридиану α.

Касательная к поверхности вращения плоскость Е определяется двумя пересекающимися прямыми t hи tα.

Пример 2. Построить плоскость Е, касательную к поверхности конуса в его точке М (рисунок 10-5).

Так как конус – поверхность линейчатая, то, проведя через точку М образующую t (являющуюся в то же время и касательной), получим одну из прямых, определяющих искомую плоскость Е. Второй прямой будет касательная t hк окружности на поверхности конуса h в ее точке М.

Отметим, что касательная t h параллельна касательной t 1, проведенной в точке N к окружности основания конуса. Поэтому искомую касательную плоскость Е можно задать образующей t и касательной t 1, не строя вспомогательной окружности h, проходящей через точку М.

Пример 3. Построить касательную к цилиндрической поверхности плоскость Е, проходящую через точку А, расположенную вне поверхности цилиндра (рисунок 10-6).

Поскольку искомая касательная плоскость должна содержать в себе образующую цилиндрической поверхности, то в качестве первой прямой, определяющей касательную плоскость, можно провести через данную точку А прямую α параллельную образующей цилиндра.

Если теперь провести через точку В (точку пересечения прямой α с плоскостью Г) касательные к окружности основания цилиндра прямые t1 и t2, то прямая α и касательные t1 и t2 определят две касательные плоскости Е(α х t1) и К(α х t2). Эти плоскости касаются поверхности цилиндра с разных сторон по его образующим т1 и т2.