Системы линейных уравнений

Глава 1. Элементы линейной алгебры

Алгебра – часть математики, посвященная изучению алгебраических операций. Термин «Алгебра» происходит от названия сочинения Мухаммеда аль-Хорезми «Альджебр аль-мукабала» (9 в.), содержащего общие приемы для решения задач, сводящихся к решению алгебраических уравнений 1-й и

2-й степеней. Ф. Виет (конец 16 в.) первым стал применять буквенные обозначения, как для неизвестных, так и для заданных в задаче величин. К середине 17 века в основном сложилась современная алгебраическая символика и тем самым завершилась «предыстория» алгебры. Исторически первым разделом алгебры была теория линейных уравнений, в которой в связи с решением систем линейных уравнений возникает понятие определителя. В 1750 году Г. Крамер публикует свои формулы для решения квадратных систем линейных уравнений. Затем появляется понятие матрицы, и в 1849 году К. Гаусс открывает свой метод решения этих систем. В 1877 году вводится понятие ранга матрицы, которое позволило явно выразить условия совместности систем линейных уравнений. (см. ниже теорему Кронекера-Капелли).

 

Числовые матрицы

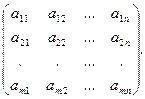Определение 1. Числовой матрицей называется прямоугольная таблица чисел

 

Числа a_ij называются элементами матрицы. Для краткости матрицы обозначаются большими буквами А, В, С (возможно с числовыми индексами), или следующим образом: (a_ij), i = 1,..., m; j = 1,..., n. Запись m ´ n называется видом матрицы, где m - число строк и n - число столбцов этой матрицы. При этом понятия строки и столбца очевидны.

Пример 1. Матрицы и их виды:

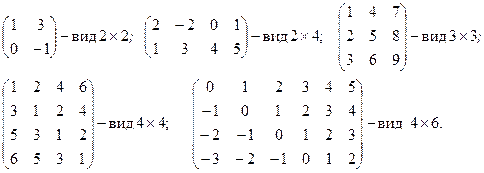
Матрица, все элементы которой равны 0, называется нулевой, обозначение: 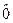. Если в матрице одинаковое число строк и столбцов (m = n), то она называется квадратной, в такой матрице элементы a ₁₁, a ₂₂,..., a_nn называются диагональными. Квадратная матрица вида n ´ n, у которой диагональные элементы равны 1 и остальные элементы равны 0, называется единичной матрицей n-го порядка и обозначается E_n:

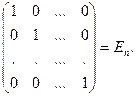Матрицы А и В называются равными, если они одинакового вида и на соответствующих местах у них стоят одинаковые числа, обозначение: A = B.

Первое очевидное и наиболее широкое применение матриц – это использование матриц для записи и передачи числовой информации при описании или исследовании каких-либо массовых явлений или процессов. При этом исходные числовые данные соответствующим образом систематизируются и записываются в виде числовой матрицы. Тем самым, автоматически происходит классификация информации (по строкам или столбцам), а это позволяет оперативно и достаточно наглядно производить внешний анализ исследуемого явления или процесса.

Пример 2. Матрицей может быть представлена информация о взаимных поставках продукции отраслей материального производства. Пусть следующая матрица А определяет взаимные поставки продукции трех отраслей:

1) химической промышленности, 2) станкостроения, 3) электроэнергетики,

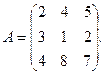Здесь элементы а ₁₁ = 2, а ₁₂ = 4, а ₁₃ = 5 означают объемы продукции химической промышленности, потребляемые соответственно в химической промышленности, станкостроении, электроэнергетике; а ₂₁ = 3, а ₂₂ = 1, а ₂₃ = 2 - объемы продукции станкостроения, потребляемые соответственно в химической промышленности, станкостроении, электроэнергетике; а ₃₁ = 4, а ₃₂ = 8, а ₃₃ = 7 - объемы продукции электроэнергетики, потребляемые соответственно в химической промышленности, станкостроении, электроэнергетике. Сравнение строчек этой матрицы показывает, что электроэнергетика является наиболее ёмкой, а станкостроение наименее ёмкой среди этих отраслей. Сравнение столбцов показывает, что продукция химической промышленности является наименее востребованной.

Пример 3. Матрицей можно представлять информацию о нормах материальных затрат для планирования снабжения предприятия. Пусть следующая матрица В определяет нормы затрат трех видов сырья на производство трех типов некоторой продукции:

 

Тогда, например, элементы а ₁₁ = 2, а ₁₂ = 0, а ₁₃ = 5 означают нормы расхода 1-го вида сырья на производство 1-го, 2-го и 3-го типов продукции, при этом а ₁₂ = 0 означает, что 1-й вид сырья не используется в производстве 2-го типа продукции.

Пример 4. С каждым человеком связан набор его социальных данных: пол, возраст, рост, вес, образование, адрес, черты характера и т. п. Тогда, например, студента Ивана Петрова можно охарактеризовать матрицей-строкой вида:

(муж.пол, 17 лет, 172 см, 67 кг, ул. Червонная 8-2, холерик).

Набор таких сведений о каждом из 25 студентов некоторой группы, записанный в виде таблицы, является матрицей вида 25´6. Теперь, например, можно ввести суммарные или средние показатели по столбцам и производить некоторые сравнения подобных групп по указанным данным.

Но очевидно, что более глубокий анализ изучаемого явления или процесса с помощью математики требует введения специальных операций над матрицами и установления связи матриц с другими математическими понятиями. Поэтому ниже определяются основные операции над матрицами, и показывается, что матрицы широко применяются при решении систем линейных уравнений и при описании линейных пространств и линейных преобразований.

Пусть А = (a_ij) и В = (b_ij), i = 1,..., m, j = 1,..., n, матрицы одинакового вида. Произведением матрицы A на число k называется матрица kA, элементы которой получаются путем умножения всех элементов матрицы А на число k:

kA = (k×a_ij), i = 1,..., m, j = 1,..., n.

Матрица (-1)· A называется противоположной для А и обозначается через – А. Суммой матриц А и В называется матрица А + В, элементами которой являются суммы соответствующих элементов этих матриц:

А + В = (a_ij + b_ij), i = 1,..., m, j = 1,..., n.

Аналогично, разностью матриц А и В называется матрица

А – В = (a_ij – b_ij), i = 1,..., m, j = 1,..., n.

Транспонированной матрицей для А называется матрица A^T, в которой каждая i -я строка матрицы А становится i -м столбцом и каждый j -й столбец становится j -й строкой:

A^T = (a_ji), i = 1,..., m, j = 1,..., n.

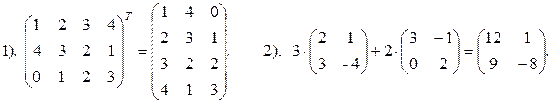Пример 5. Выполнить следующие действия над матрицами.

 

Произв дение двух матриц. Рассматриваются матрицы А = (а_ik), i = 1,..., m, k = 1,..., l, вида m ´ l и В = (b_kj), k = 1,..., l, j = 1,..., n, видa l ´ n. При умножении А на В получается матрица А × B = (c_ij), i = 1,..., m, j = 1,..., n, вида m ´ n, элементы которой c_ij вычисляются по формуле:

с_ij = a_{i 1}× b _{1 j} + a_{i 2}× b _{2 j} +... + a_il × b_lj.

Это сумма произведений элементов i -й строки на соответствующие элементы j -го столбца. Обратите внимание на то, что число столбцов первой матрицы А должно быть равно числу строк второй матрицы В, при нарушении этого условия матрицы нельзя умножать.

Пример 6. Выполнить умножение матриц.

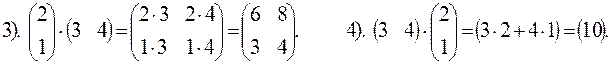Для введенных операций над матрицами выполняются многие свойства аналогичные свойствам арифметических операций над числами. Например, верны следующие равенства (справа указаны названия свойств, выражаемых этими равенствами):

1. A + В = В + А;(коммутативность сложения)

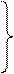2. А + (В + С) = (А + В) + С;

3. k (А × В) = (kА × В) = (А × kВ); (ассоциативность)

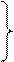4. А ×(В × С) = (А × В)× С;

6. k ×(A + B) = k × A + k × B. (дистрибутивность)

7. (A + B)× C = A × C + B × C.

8. А – А = 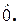(свойство противоположных матриц)

9. E_n × A = A × E_n = A. (свойство единицы)

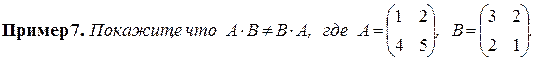С другой стороны, умножение матриц существенно отличается от умножение чисел, например: произведение А × В может отличаться от В × А, и произведение ненулевых матриц может равняться нулевой матрице.

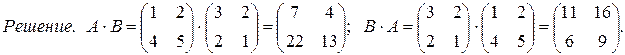
В результате выполненных действий получены различные матрицы, что и требовалось показать.

Пример 8. Выполнить умножение матриц:

 

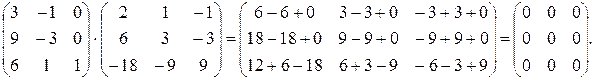
Определители матриц

Каждой квадратной матрице А ставится в соответствие число, называемое определителем и обозначаемое | A | или det (A). Сначала вводятся определители первого, второго и третьего порядков.

Определитель 1-го порядка матрицы 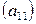равен единственному элементу этой матрицы:

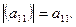
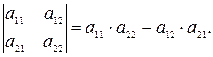Определитель 2-го порядка матрицы 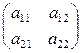определяется следующим образом:

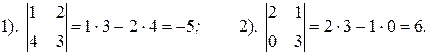Пример 9. Вычислить определители 2-го порядка:

Определитель 3-го порядка матрицы вида 3´3 вычисляется по формуле:

 

Здесь каждое слагаемое является произведением трех элементов матрицы, составленное так, что в него входит по одному элементу из каждой строки и каждого столбца. Рассматриваются всевозможные такие комбинации элементов, а знаки слагаемых зависят от четности или нечетности перестановок, образуемых индексами входящих в них множителей. Понятие перестановки в данном курсе не рассматривается, поэтому эту формулу нужно просто запомнить. Следующая схема вычисления определителя 3-го порядка облегчает запоминание этой формулы. К данному определителю снизу приписываются две первые строки:

+ а ₁₁ а ₁₂ а ₁₃ -

+ а ₂₁ а ₂₂ а ₂₃ -

+ а ₃₁ а ₃₂ а ₃₃ -

а ₁₁ а ₁₂ а ₁₃

а ₂₁ а ₂₂ а ₂₃

Теперь, слагаются произведения трех чисел, стоящих на главных диагоналях (слева-направо-вниз), и вычитаются произведения трех чисел, стоящих на побочных диагоналях (справа-налево-вниз):

а ₁₁× а ₂₂× а ₃₃ + а ₂₁× а ₃₂× а ₁₃ + а ₃₁× а ₁₂× а ₂₃- а ₁₃× а ₂₂× а ₃₁ - а ₂₃× а ₃₂× а ₁₁ - а ₃₃× а ₁₂× а ₂₁.

Такая схема вычисления верна только для определителей 3-го порядка.

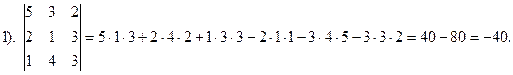Пример 10. Вычислить следующие определители:

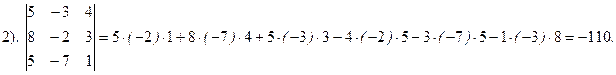Выше было замечено, что определитель 3-го порядка равен алгебраической сумме всевозможных произведений трех элементов матрицы, составленных так, что в каждую тройку входит по одному элементу из каждой строки и каждого столбца матрицы. При этом эти произведения снабжаются дополнительными знаками + или - по определенным правилам, которые в данном курсе не рассматриваются. Таким же способом определяются определители n -го порядка для n = 4, 5, …. [8. с. 445]. Это определение так же не рассматривается, а вместо него описывается основное правило вычисления определителей с помощью теоремы Лапласа. Для формулировки этой теорема вводятся следующие понятия.

Определение 2. Минором элемента a_ij квадратной матрицы А называется определитель матрицы, получаемой из А вычеркиванием i -й строки и j -го столбца, обозначение: . Алгебраическим дополнением элемента a_ij называется произведение его минора на (-1) ^i+j, обозначение: А_ij.

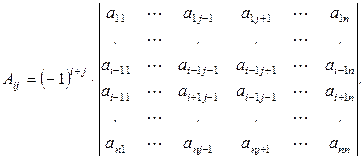
Пример 11. Вычислить алгебраические дополнения элементов второй строки следующей матрицы А: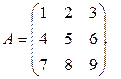

Решение:

Ответ: А ₂₁ = 6, А ₂₂ = -12, А ₂₃ = 6.

Следующая теорема дает метод вычисления определителей 4-го и более высокого порядков.

Теорема Лапласа. 1). Сумма произведений элементов какой-либо строки (или столбца) на их алгебраические дополнения равна определителю матрицы:

a_{i 1} × A_{i 1}+ a_{i 2} × A_{i 2}+... + a_in × A_in =ï A ï; a _{1 j} × A _{1 j} + a _{2 j} × A _{2 j} +... + a_nj × A_nj =ï A ï.

2). Сумма произведений элементов какой-либо строки (или столбца) на алгебраические дополнения соответствующих элементов другой строки (или другого столбца) равна нулю:

a_{i 1} × A_{j 1} + a_{i 2} × A_{j 2} +... + a_in × A_jn = 0; a _{1 i} × A _{1 j} + a _{2 i} × A _{2 j} +... + a_ij × A_nj = 0.

Доказательство (см. [8. с. 449]).

Первая формула называется разложением определителя по i-й строке, вторая формула - разложение определителя по j-му столбцу. Формулы второй части носят вспомогательный характер.

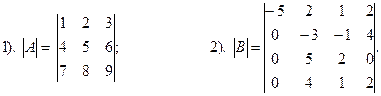Пример 12. Вычислить определители:

Решение. 1). Используется разложение определителя по второй строке и вычисления в примере 11.

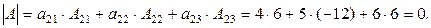
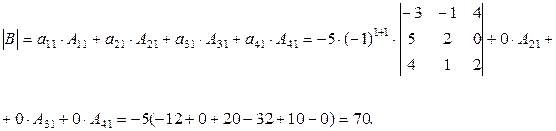2). В 1-м столбце много нулей, поэтому применяется формулу разложения определителя по 1-му столбцу:

Свойства определителей

1. При транспонировании матрицы ее определитель не изменяется.

2. Если в определителе поменять местами две строки (или два столбца), то он изменит только знак.

3. Если определитель содержит две одинаковые строки (или столбца), то он равен нулю.

4. Если определитель содержит строчку (или столбец), состоящую из нулей, то он равен нулю.

5. Если элементы какой-либо строки (или столбца) определителя умножить на одно и то же число, то и определитель умножится на это число.

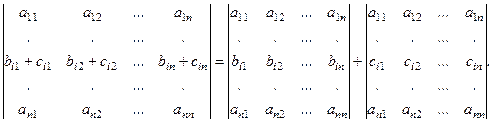6. Если элементы какой-либо строки (или столбца) определителя являются суммами двух чисел (b_{i 1} +c_{i 1}, b_{i 2} +c_{i 2}, …, b_in+c_in), то имеет место следующее равенство:

 

7. Если к элементам какой-либо строки (или столбца) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и то же число, то определитель не изменится.

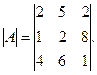Доказательство (см. [1. с. 152]).

Пример 13. Вычислить определитель, применяя указанные свойства.

Решение. Сначала определитель преобразуется так, чтобы в 1-м столбце было два нуля. Для этого применяется свойство 7, согласно которому определитель не изменится в результате следующих преобразований. Элементы второй строки умножаются на (-2) и прибавляются к соответствующим элементам первой строки; затем элементы второй строки умножаются на (- 4) и прибавляются к соответствующим элементам третьей строки. Получается равный определитель, который разлагается по 1-м столбцу.

Обратная матрица

Определение 3. Пусть А - квадратная матрица вида n´n, тогда обратной матрицей для А называется матрица (обозначение: А ^-1), которая при умножении на А слева и справа дает единичную матрицу Е_n:

 

А × А ^-1 = А ^-1× А = Е_n. (1)

Для матрицы А = 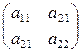вида 2´2 обратную матрицу А ^-1 можно находить по формуле: А ^-1 = 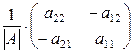, (см. ниже пример 15).

Квадратная матрица называется вырожденной, если ее определитель равен нулю; а если определитель матрицы не равен нулю, то она называется невырожденной.

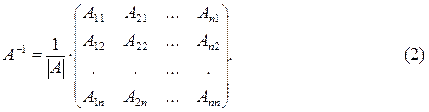Теорема 1. Невырожденная матрица А имеет единственную обратную матрицу А ^-1, и верна формула

Доказательство (см. [1. с. 188]).

 

Стоящая здесь матрица составлена из алгебраических дополнений элементов исходной матрицы и называется присоединенной [1, с.189].

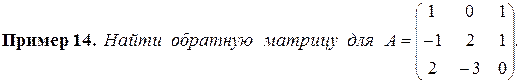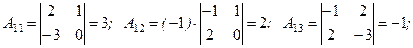Решение. Указанными выше методами находится определитель ï A ï= 2. Так как ï A ï ¹ 0, то A -невырожденная, и имеет обратную матрицу. Для ее построения вычисляются алгебраические дополнения:

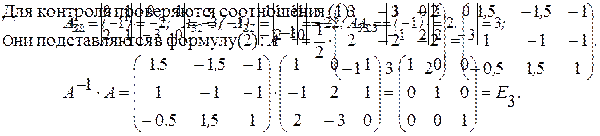Равенство А^{- 1} × А = Е ₃выполняется, второе равенство А × А^{- 1} = Е ₃ будет выполняться автоматически. Ответ:

Пусть А, В – матрицы и Х – буква, тогда равенство А × Х = В называется матричным уравнением. Если А имеет обратную матрицу А ^-1, то решение этого уравнения находится с помощью умножения слева обеих частей на А ^-1:

А ^-1×(А × Х)= А ^-1× В. Получается: Х = А ^-1× В - это решение данного уравнения.

Если матричное уравнение имеет вид Х × А = В, то его решение имеет вид:

Х = В × А ^-1.

 

Пример 15. Решить матричные уравнения:

Решение. 1). В первом уравнении А= 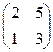, | A | = 2×3- 5×1= 1, А ^-1 = 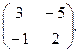Тогда Х = А ^-1× В =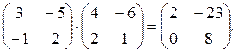

2). Во втором уравнении А = 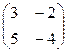, | A | = -2, А ^-1 = = 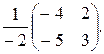Тогда

Х = В × А ^-1=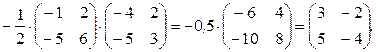

Системы линейных уравнений

Уравнение – это равенство, которое содержит буквы, обозначающие неизвестные величины, эти буквы называются неизвестными. Решением уравнения называется упорядоченный набор чисел, при подстановке которых в уравнение вместо соответствующих неизвестных получается верное равенство. Решить уравнение, значит, найти множество всех его решений.

Определение 4. Системой линейных уравнений называется набор уравнений следующего вида:

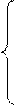а ₁₁ х ₁ + а ₁₂ х ₂ +... + а _{1 n} х_n = b ₁,

а ₂₁ х ₁ + а ₂₂ х ₂ +... + а _{2 n} х_n = b ₂,

.............................................. (3)

а_{m 1} х ₁ + а_{m 2} х ₂+... + а_mnх_n = b_m,

где а_ij - числовые коэффициенты, b_i - свободные члены, х _j - неизвестные, i = 1,…, m, j = 1,…, n.

Отличительная черта линейных систем в том, что к неизвестным применяются только линейные операции - алгебраическое сложение и умножение на число. Решением системы (3) называется упорядоченный набор значений неизвестных(х ₁, х ₂,..., х_n), при подстановке которых в каждое уравнение получаются верные равенства. Система, имеющая хотя бы одно решение, называется совместной; система, не имеющая решений, называется несовместной; система, имеющая единственное решение, называется определенной; система, имеющая более одного решения, называется неопределенной. Если в системе (3) все свободные члены равны нулю, то она называется однородной. Системы, имеющие одинаковые множества решений называются равносильными. Для обозначения равносильныъх систем используются символы Û или «.

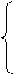Пример 16. Какой набор чисел (1; -2; -7) или (3; 1; 0) является решением системы: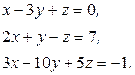

Решение. Нужно подставить каждую тройку чисел вместо x, y, z в эти уравнения:

1) 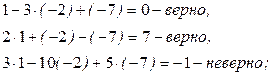2)

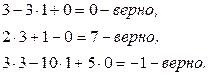
Ответ: (1; -2; -7) не является решением, (3; 1; 0) является решением.

Системы двух уравнений с двумя неизвестными имеюи вид:

а ₁₁ х ₁ + а ₁₂ х ₂ = b ₁,

а ₂₁ х ₁ + а ₂₂ х ₂= b ₂.

При решении такой системы можно использовать следующие формулы:

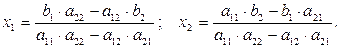
при условии, что .

Системы трех уравнений с тремя неизвестными имеют вид:

а ₁₁ х ₁ + а ₁₂ х ₂ + а ₁₃ х ₃ = b ₁,

а ₂₁ х ₁ + а ₂₂ х ₂ + а ₂₃ х ₃ = b ₂,

а ₃₁ х ₁ + а ₃₂ х ₂ + а ₃₃ х ₃ = b ₃.

Методы решения таких систем рассматриваются ниже.

Для перехода к матричной записи вводятся обозначения:

А – матрица коэффициентов при неизвестных, Х – столбец неизвестных,

В – столбец свободных членов:

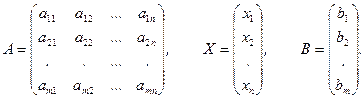Тогда система (3) записывается в следующей матричной форме

Например, матричная запись системы трех уравнений с тремя неизвестными имеет вид:

 

Методы решения систем

1. Сначала рассматривается метод Крамера для решения систем специального вида, когда число уравнений равно числу неизвестных, такие системы называются квадратными:

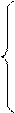а ₁₁ х ₁ + а ₁₂ х ₂ +... + а _{1 n}х _n = b ₁,

а ₂₁ х ₁ + а ₂₂ х ₂ +... + а _{2 n} х_n = b ₂,

........................................... (5)

а_{n 1} х ₁ + а_{n 2} х ₂ +... + а_nnх_n = b_n.

Теорема Крамера. Пусть А – матрица коэффициентов в квадратной системе (5). Тогда:

1) если определитель ï А ï не равен нулю, то система (5) имеет единственное решение, которое находится по следующим формулам

где и D _i - вспомогательные определители, получаемые из ï А ï путем замены i-го столбца на столбец В свободных членов:

D _i = 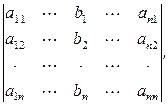i = 1,..., n;

2) если определитель ï А ï равен нулю и хотя бы один из D _i отличен от

нуля, то система (5) не имеет решений;

3) если определитель ï А ï и все вспомогательные определители D _i равны нулю, то система (5) имеет бесконечное множество решений.

Доказательство (см. [1. с. 163]).

x + 2 y + z = 8,

Пример 17. Решить методом Крамера систему 3 x + 2 y + z = 10,

4 x + 3 y - 2 z = 4.

Решение. Сначала находится определитель 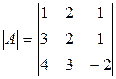= 14.

Так как ï А ï¹ 0, то система имеет единственное решение, которое находится по формулам (6). Для этого находятся вспомогательные определители:

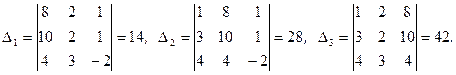Тогда получается: х = 14:14 = 1; у = 28:14 = 2; z = 42:14 = 3.

Ответ: х = 1; у = 2; z = 3.

2. Второй метод называется методом Гаусса. Он применяется к любым системам вида (3) и использует так называемые эквивалентные преобразования систем, которые, по определению, не изменяют множество решений системы. Такими преобразованиями являются:

а) перестановка уравнений;

б) умножение уравнения на число, отличное от нуля;

в) сложение уравнений.

С помощью этих преобразований система (3) приводится к так называемому виду трапеции:

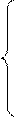а ₁₁^* х ₁ + а ₁₂^* х ₂ +... + а _{1 k} ^* х_k +... + а _{1 n} ^* х _n = b ₁^*,

а ₂₂^* х ₂ +... + а _{2 k} ^* х_k +... + а _{2 n} ^* х_n = b ₂^*,

….......................................... (7)

а_mk ^* х_k +... + а_mn ^* х_n = b_m ^*.

Здесь b_i^*, a_ij^*- уже другие числа, полученные в результате указанных преобразований, но эта система равносильна исходной системе (3).

Если в полученной системе (7) число уравнений равно числу неизвестных, то она называется треугольным видом исходной системы. В ходе преобразований уравнений системы могут возникать равенства следующих видов:

1) 0 = 0, (такое равенство отбрасывается, при этом число уравнений уменьшается);

2) 0 = b, где b ¹ 0, (в этом случае говорят, что получено противоречие и потому система не имеет решений).

Теорема Гаусса. Пусть система (3) эквивалентными преобразованиями приведена к виду (7). Тогда:

1) если в (7) нет противоречий и число уравнений равно числу неизвестных, то система (3) имеет единственное решение;

2) если (7) содержит противоречие, то система (3) не имеет решений;

3) если в (7) нет противоречий, но число уравнений меньше числа неизвестных, то система (3) имеет бесконечное множество решений.

Доказательство (см. [1. с. 169]).

Метод Гаусса наиболее важен для практики и по сравнению с другими методами имеет следующие достоинства:

1) он менее трудоемкий, позволяет легко установить, является ли данная система совместной или несовместной;

2) в случае совместности системы он позволяет легко определить, является ли данная система определенной или неопределенной;

3) в случае определенной системы, ее единственное решение вычисляется с помощью несложной процедуры, (см. пример 18);

4) в случае неопределенной системы он позволяет легко построить так называемые базисные решения, с помощью которых описывается множество всех решений данной системы, (см. ниже §6).

3 x + 2 y + z = 10,

Пример 18. Решить методом Гаусса систему x + 2 y + z = 8,

4 x + 3 y - 2 z = 4.

Решение.1-й шаг. На первое место переставляется уравнение, в котором коэффициент при первой неизвестной х не равен 0 и является наиболее удобным для дальнейших преобразований. Здесь во 2-м уравнении коэффициент при х равен 1, поэтому меняются местами 1-е и 2-е уравнения:

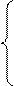x + 2 y + z = 8,

3 x + 2 y + z = 10,

4 x + 3 y - 2 z = 4.

2-й шаг. 1-е уравнение умножается на -3 и прибавляется ко 2-му уравнению, затем опять 1-е уравнение умножается на -4 и прибавляется к 3-му уравнению, получается равносильная система

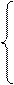х + 2 y + z = 8,

-4 y - 2 z = -14,

-5 y - 6 z = -28.

3-й шаг. 2-е уравнение умножается на -5, 3-е уравнение умножается на 4, и получается равносильная система:

х + 2 y + z = 8,

20 y + 10 z = 70,

-20 y - 24 z = -112.

4-й шаг. К 3-му уравнению прибавляется 2-е уравнение и получается система в треугольном виде:

 

 

х + 2 y + z = 8,

20 y + 10 z = 70,

-14 z = -42.

5-й шаг. Полученная система не содержит противоречий, и в ней число уравнений равно числу неизвестных. Следовательно, исходная система имеет единственное решение, которое находится следующим образом. Из 3-го уравнения находится значение для z: z = -42:(-14) = 3. Это значение подставляется во 2-е уравнение и находится значение для у: у = (70 -10×3):20 = 2. Далее, найденные значения z = 3, у = 2 подставляются в 1-е уравнение, и находится значение х: х = 8 - 2×2 - 3 = 1.

Ответ: х = 1, у = 2, z = 3.

Другие из указанных выше достоинств этого метода будут рассмотрены в следующем параграфе.

Иногда метод Гаусса описывают с использованием матричной записи (4) данной системы. При этом вместо уравнений производят преобразование так называемой расширенной матрицы:

А * = 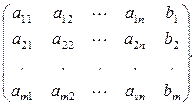(8)

Допускаются следующие три преобразования: а) перестановка строк, б) умножение строк на число, отличное от нуля, в) сложение строк. С помощью этих преобразований расширенная матрица приводится к виду трапеции:

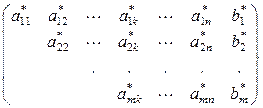(9)

По этой матрице восстанавливается система (7) и производятся указанные выше действия.

3. Третий метод матричный, он применяется к квадратным системам вида (5), использует их матричную форму записи (4) и основан на следующих рассуждениях. Пусть А × Х = В – матричная форма системы (5), при этом матрица А имеет обратную матрицу А ^-1. При умножении слева обеих частей данного матричного равенства на обратную матрицу получается равенство: А ^-1×(А × Х) = А ^-1× В. Отсюда, согласно матричным свойствам 7, 8 и соотношению (1), последовательно получаются равенства:

(А ^-1× А)× Х = А ^-1× В, Е_n × Х = А ^-1× В, Х = А ^-1× В.

Последнее равенство Х = А ^-1× В есть матричная запись решения системы.

x + 2 y + z = 8,

Пример 19. Решить систему уравнений 3 x + 2 y + z = 10,

4 x + 3 y - 2 z = 4,

с помощью обратной матрицы.

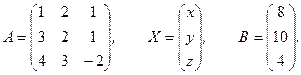
Решение. Сначала вводятся следующие обозначения:

Тогда система запишется в виде: А × Х = В, ее решение имеет вид Х = А ^-1× В.

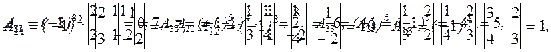Находится обратная матрица А ^-1. Определитель ï А ï=14 был найден в примере 3, тогда находятся алгебраические дополнения и применяется формула (2).

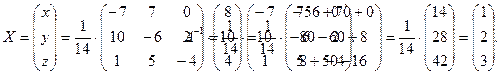Ответ: x = 1, y = 2, z = 3.

Системы линейных уравнений возникают при решении многих задач линейного программирования, которые имеют большое практическое применение. В следующем примере рассматривается наиболее простая задача такого вида.

Пример 20. В производстве трех типов продукции используются три вида сырья А, В, С. Нормы затрат сырья на производство единицы каждого типов продукции и запасы сырья даны в следующей таблице.

Тип продукции Вид сырья	Нормы затрат	Запасы
1-й тип	2-й тип	3-й тип
А
В
С

Требуется определить план производства, обеспечивающий использование всего сырья.

Решение. Пусть х ₁, х ₂, х ₃ - количество единиц продукции 1-го, 2-го, 3-го типов соответственно, которое должно выпустить предприятие. Тогда расход сырья А равен произведению количества единиц каждого типа продукции на соответствующие нормы затрат этого сырья: 2 х ₁ + 3 х ₂ + х ₃. Это должно равняться его запасам 245, получается первое уравнение: 2 х ₁ + 3 х ₂ + х ₃ = 245. Аналогично получаются уравнения для сырья В и С, и задача сведена к решению следующей системы линейных уравнений:

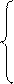2 х ₁ + 3 х ₂

Поделиться: