Применение определенных интегралов

Неопределенный интеграл

 

Интегрирование – это операция, при которой по производной некоторой функции восстанавливается сама функция, т. е. это - операция, противоположная диффе­ренцированию. Для более строгого определения этой операции вводятся следующие понятия.

Определение 1. Первообразной функции f (x) на некотором ин­тервале (a; b) называется функция F (x), производная которой равна f (x) на этом интервале, т. е. для любого х Î(a; b) выполняется равенство:

F ¢(x) = f (x). (48)

Пример 1. а). Пусть f (x) = 3 х ², тогда первообразная равна F (x) = х ³.

Проверка: F¢ (x) = (х ³)′ = 3 х ² = f (x) - верно.

б). Пусть f (x) = е ^{2 х +3}, тогда первообразная равна F (x) = 0,5 е ^{2 х +3}.

Проверка: F¢ (x) = (0,5 е ^{2 х +3})′ = 0,5∙2 е ^{2 х +3} = е ^{2 х +3} = f (x), верно.

Следующие два свойства дают основной способ описания всех первообразных данной функции.

Свойство 1. Если F (x) – первообразная функции f (x) на (a; b), то для любого числа с функция F (x) + с так же является первообразной функции f (x) на (a; b).

Доказательство. Пусть F (x) – первообразная функции f (x) на (a; b), тогда верно равенство (48), и для любого числа с выполняются равенства:(F (x) + с)¢ = F¢ (x) + с¢ = f (x). Таким образом, функция F (x) + с удовлетворяет (48), поэтому она является первообразной f (x). Свойство доказано.

Свойство 2. Если F ₁(x) и F ₂(x) – первообразные одной и той же функции, то эти функции отличаются друг от друга на постоянное число: F ₁(x) – F ₂(x) º с.

Доказательство. Пусть F ₁(x) и F ₂(x) – первообразныефункции f (x), тогда каждая из них удовлетворяет равенству (48), и выполняется тождество: (F ₁(x) - F ₂(x))¢= f (x) - f (x) º 0. Следовательно, по теореме 3 из §5 главы 5, разность F ₁(x) - F ₂(x) есть постоянное число, что и требовалось доказать.

Согласно этим свойствам, все первообразные функции f (x) имеют вид F (x) + с, где F (x) – некоторая первообразная этой f (x) и с – произвольное число. Поэтому формула F (x) + с описывает множество всех первообразных функции f (x).

Определение 2. Неопределенным интегралом функции f (x)на­зывается множество всех первообразных этой функции.

Обозначение: ò f (x) dx. В этой записи первый символ ò называется интегралом, f (x) – подынте­гральная функция, х – переменная интегрирования, dx – дифференциал х.

В силу свойств первообразных, имеет место следующее равенство:

ò f (x) dx = F (x) + c, (49)

где F (x) – некоторая первообразная функции f (x) и c – символ константы.

Если функция f (x) имеет первообразную на интервале (a; b), то она называется интегрируемой на (a; b).

В следующей таблице указаны основные формулы для нахождения интегралов от элементарных функций. Эти формулы называются табличными интегралами.

Таблица основных интегралов

1. ò xⁿ dx = , если n ¹ -1; в частности:

2. ò dx = ln | x |+ c; в частности:

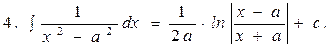3. в частности:

6.

7.

8.

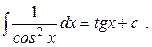
9.

Для проверки этих формул нужно вычислить производную от правой части и убедиться, что в результате получается подынтегральная функция.

Пример 2. Доказать интеграл ò xⁿ dx = , где n ¹ -1.

Доказательство. Вычисляется производная от правой части: = + 0 = xⁿ. Получилась подынтегральная функция, интеграл доказан.

Свойства интегралов

1). Производная от интеграла по переменной интегрирования равна подынтегральной функции: (ò f (x) dx)¢= f (x).

2). Интеграл от дифференциала функции равен самой функции:

ò du = u + c.

3). Если функции f (x)и g (x)интегрируемы, то сумма этих функций

интегрируема, и верно равенство:

4). Если функция f (x)интегрируема, то для любого числа с произведение c × f (x) интегрируемо и верно равенство:

ò c × f (x) dx = c ×ò f (x) dx.

Доказательство. Согласно равенствам (48) и (49), (ò f (x) dx)¢= (F (x) + c)¢= f (x), следовательно, свойство 1) доказано. Аналогично доказывается свойство 2). Далее, в силу свойств производной и свойства 1),

()¢ = = .

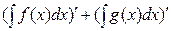Следовательно, свойство 3) доказано. Аналогично доказывается свойство 4).

В следующих примерах подынтегральная функция преобразовывается в сумму табличных интегралов и затем применяются свойства 3), 4). Этот метод называется методом разложения. Для краткости исходные инте­гралы обозначаются символом ò.

Пример 3. Найти следующие интегралы.

1). ò (x ³ - 3 x ² + 2 x – ) dx.

По указанным выше свойствам и формулам 1, 2 таблицы интегралов, ò = ò x ³ dx - 3ò x ² dx + 2ò x dx – 4ò dx = 0, 25х⁴ - х ³ + х ² – 4× ln | x |+ c.

2). ò (x ² – 2)² dx.

Раскрываются скобки и, по формуле 1, получается: ò = ò(x ⁴ - 4 x ² + 4) dx = x ⁵ - x ³ + 4 x + c.

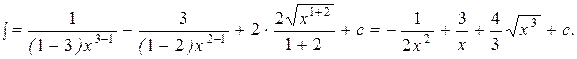Применяются вспомогательные формулы а), б) из пункта 1 таблицы интегралов:

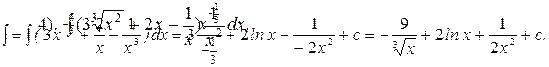Каждое слагаемое в скобках умножается на , получен­ные выражения интегрируются, как в предыдущих примерах:

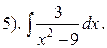Применяется формула 4:

В более полных курсах по математике доказывается следующее ут­верждение.

Теорема 1. Если функция f (x) непрерывна или имеет только конечное число конечных разрывов на некотором интервале, то она интегрируема в этом интервале.

Согласно теореме 1 из §4 главы 4, всякая элементарная функция непрерывна там, где она определена. Поэтому она имеет первообразную в своей области определения. Но не всегда эта первообразная является элементарной функцией. Например, следующие интегралы от элементарных функций существуют, но не являются элементарными функциями:

Такие интегралы называются неберущимися, они вычисляются с помощью специальных методов, которые в данном курсе не рассматриваются. Здесь изучаются только некоторые методы интегрирования, которые дают элементарные функции.

Методы интегрирования

 

1. Метод введения нового аргумента. Если 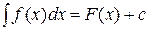, то . Более того, если функция u = j (x) - непрерывно диффе­ренцируемая функция, то , и в таких случаях допускается запись вида:

Пример 4. Найти интегралы.

1). ò(1 + х)⁴ dx.

Ясно, что dx = d (x +1), поэтому пусть u = (x +1), тогда

ò = ò(1 + х)⁴ d (х +1) = ò u ⁴ du = + с = + с.

2). ò 2 х (х ² +1)³ dx.

Здесь d (x ² +1) = 2 xdx, поэтому пусть u = (x ² +1), тогда

 

Здесь d (x ² +3 х- 5) = (2 x + 3) dx, поэтому пусть u = (x ² +3 х- 5), тогда

2. Метод подстановки. Пусть функция x = j(t) монотонна и непрерывно дифференцируема в интервале (a; b), и функция f (x) непрерывна в интервале (а; b), где а = j(a), b = j(b). Тогда верна формула

 

ò f (x) dx = ò f (j(t))×j¢(t) dt. (50)

 

Пример 5. Найти следующие интегралы.

1). ò е^{- 3 х} dx. Этот интеграл сводится к табличному интегралу 3 заменой: -3 х = t. Отсюда х = - , х ¢= (- )¢= - . Тогда, по формуле (50), данный интеграл равен ò е^t ×(- ) dt = (- )× е^t + c. Теперь, делается обратная замена t на –3 х, и получается:ò= - × е ^{- 3 х} + c.

Делается замена: 2 х - 1= t, отсюда: х = , dx = dt, х -1 = , . Тогда

Делается замена: ln x = t, отсюда x = e^t, dx = e^t × dt. Тогда

4).

Выделяется полный квадрат в знаменателе: х ² +4 х +3 =(х ² +4 х +4) - 1

= (х + 2)²-1. Делается замена: (х + 2) = t, отсюда dx = dt и х ² + 4 х +3 = t² - 1.

3. Метод интегрирования по частям. Если u и v - дифференцируемые функции от х, то верно равенство

ò u dv = u× v - ò v du. (51)

Эта формула применяется в случаях, когда подынтегральная функция является произведением алгебраической и трансцендентной функций, напри­мер, ò хⁿ × е^х dх или ò хⁿ × lnx dх. При этом, в интеграле ò хⁿе^хdх в качестве u нужно при­нять хⁿ, и тогда dv = е^хdх, а в интеграле ò хⁿlnxdх в качестве u нужно принять lnx, и тогда dv = хⁿdх.

Пример 6. Найти следующие интегралы.

1). ò х × ln (x +1) dх.

Применяется метод интегрирования по частям. Пусть u = ln (x +1) и dv = х dх, тогда du =(ln (x +1))¢ dх = dх, v =ò х dх = , (здесь можно считать, что с = 0). Теперь, применяется формула (51):

2). ò х × е^{- 2 х} dх. Применяется метод интегрирования по частям. Пусть u = x и dv = е^{- 2 х} dх, отсюда du = dх, v =ò е^{- 2 х} dх = - × е^{- 2 х} (этот интеграл находится так же, как интеграл примера 5.1)). Теперь, применяется формула (51): ò = х ×(- )× е^{- 2 х} -ò (- )× е^{- 2 х} dх = - хе^{- 2 х} - е^{- 2 х} + с.

4. Интегрирование рациональных функции. Следующие функции называются простейшими рациональными дробями:

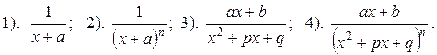
Интегрирование таких функций осуществляется следующим образом.

1). 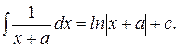2).

3). Сначала выделяется полный квадрат в знаменателе:

= =

Теперь, делается замена: , отсюда Тогда

где

=

=

=

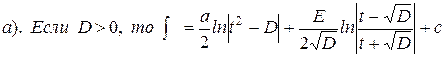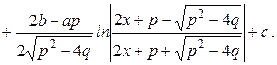
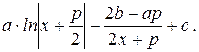
4). С помощью той же замены при n > 1 получается:

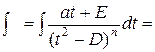
a). Первое слагаемое вычисляется с помощью замены , :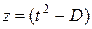

=

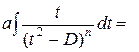
б). Второе слагаемое вычисляется методом интегрирования по частям. Пусть

. Тогда .

Пусть тогда

По формуле (51),

Получилось так называемое рекуррентное соотношение для интеграла I_n:

Этосоотношение позволяет последовательно вычислить I_n для любого n.

Пример 7. Найти следующие интегралы.

1).

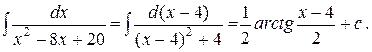
2).

=

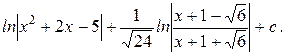
3). Здесь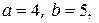

E= . Так как D < 0, то

 

+ 11

5. Интегрирование некоторых тригонометрических функций. Следующие интегралы демонстрируют основные приемы интегрирования тригонометрических функций.

1). Интегралы 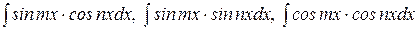используют тригонометрические формулы преобразования произведения в сумму (см. главу 4 §2).

а).

= -

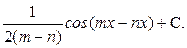
б).

= -

в).

= +

2). Интегралы используют тригонометрические формулы понижения степени, (см. главу 4 §2).

а).

б).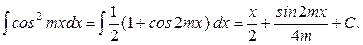

в).

3). Интегралы вида используют замены sinmx = t, cosmx = t,соответственно.

а).

б).

Определенный интеграл

Пусть функция f (x) определена на отрезке [ a; b ]. Этот отрезок разбивается на n частей точками: а = х ₀ < x ₁ < x ₂< … < x_n = b, и пусть D x ₁, D x ₂, …, D x_n - длины отрезков разбиения. Из каждого такого отрезка

(x_{i -1}; x_i) выбирается произвольная точка x _i, вычисляется значение f (x _i), и составляется сумма

S ₁= f (x₁)D x ₁ + f (x₂)D x ₂ + … + f (x _n)D x_n. (52)

Эта сумма называется интегральной суммой для f (x) на [ a; b ], более кратко она записывается в виде

S ₁= .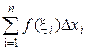

Затем, отрезки (x_{i -1}; x_i) разбиваются на более мелкие части, из них выбираются новые точки и составляется новая интегральная сумма S ₂ вида (52). Этот процесс разбиения отрезка [ a; b ] на более мелкие части, и составление соответствующих интегральных сумм продолжается бесконечно. В результате возникает бесконечная последовательность интегральных сумм: S ₁, S ₂, S ₃, ….

Определение 3. Определенным интегралом от функции f (x) в пределах от а до b называется предел указанных выше интегральных сумм, когда отрезок [ a; b ] бесконечно измельчается, если этот предел существует и не зависит от способов разбиения и выбора точек.

 

Обозначение:

Числа a, b называются пределами интегрирования.

Понятие интегральной суммы иллюстрируется на чертеже 40. Рассматривается непрерывная положительная функция y = f (x) на [ a; b ]. Ее график и ось Оx образуют криволинейную трапецию аАВb. Че­рез точки деления а, x ₁, x ₂, …, x_{n -1}, b проведены отрезки, параллельные оси О Y, и образованы прямо­угольники с основаниями и высо­тами f (x₁), f (x₂), …, f (x _n).

y f (x_n) В

f (x₂) y = f (x)

f (x₁)

А …

 

x

0 a x₁ x ₁ x₂ x _2... x_{n- 1} x _n b

Черт.40.

 

Тогда площади этих прямо­угольников равны f (x₁)D x ₁, f (x₂)D x ₂ , …, f (x _n)D x_n, соответственно, и их сумма å f (x _i)D x_i является приближенным значением площади всей кри­волинейной трапеции аАВb. Если производить более мелкие разбиения [ a; b ], то соответствующие суммы å f (x _i)D x_i будут приближаться к истинному значению площади аАВb. Поэтому площадью криволинейной трапеции аАВb назван предел указанных сумм å f (x _i)D x_i, когда отрезок [ a; b ] бесконечно измельчается. С другой стороны, эти суммы являются интегральными суммами для функции f (x) на [ a; b ]. Тем самым, получен следующий геометрический смысл определенного интеграла:

Определенный интеграл положительной функции y = f(x) по отрезку [ a; b ] равен площади криволинейной трапеции аAВb.

Свойства определенного интеграла

 

 

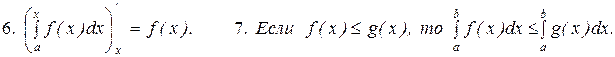
Здесь подразумевается, что интегралы, указанные в правых частях пунктов 2 - 5, существуют; и в пункте 7 неравенство функций рассматрива­ется на [ a; b ].

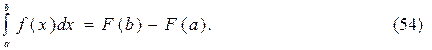Теорема 2. Пусть f (x) непрерывна на [ a; b ]. Тогда она имеет первообразную F (x) на [ a; b ] и верна формула:

 

Эта формула называется формулой Ньютона-Лейбница. Она означает, что определенный интеграл от непрерывной функции равен разности значе­ний первообразной функции при верхнем и нижнем пределах интегрирова­ния. Эта разность называется приращением F (x) на [ a; b ] и обозначается:

Пример 8. Вычислить определенные интегралы.

 

Теорема о среднем. Если функция f (x) непрерывна на [ a; b ], то между a и b найдется число с такое, что выполняется равенство:

 

Величина f (c) называется средним значением функции f (x) на [ a; b ].

Пример 9. Определить среднее значение функции у = х ² на [1; 3].

Здесь f (x) = x ² . Вычисляется интеграл:

Теперь, из теоремы о среднем, получается:

Вывод: среднее значение приближенно равно 4,667 при х » 2,1602.

Из теоремы 2 следует, что для непрерывных функций методы интег­риро­вания для неопределенного интеграла можно применять и для опреде­ленного интеграла со следующими дополнениями.

В методе интегрирования подстановкой формула (50) принимает вид:

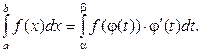(55)

В методе интегрирования по частям формула (51) принимает вид:

 

Пример 10. Вычислить следующие определенные интегралы.

Применение определенных интегралов

1. Площадь плоской фигуры (см. черт. 41), ограниченной кривыми y = f (x), y = g (x) и прямыми x = a, x = b (при этом f (x) < g (x), a < b) вычисляется по формуле:

y y = g (x)

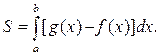y = f (x)

0 a b x

Черт.41.

2. Площадь плоской фигуры (см.черт.42), ограниченной кривыми x = F (y), x = G (y) и прямыми y = c, y = d (при этом F (y) < G (y), c < d) вычисляется по фор­муле:

y

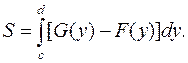d

x = F (y) x = G (y)

c

0 x

Черт.42.

Пример 11. Вычислить площадь фигуры, ограниченной линиями:

y = x ² +1, y = x, y = 5, x = 0.

Решение. y = x ² +1 – это уравнение параболы с вершиной С (0; 1);

y = x - это прямая, проходящая через начало координат под углом 45^о к оси О х; x = 0 - это ось О y. Получается фигура ОСАВ (см. черт. 43).

у

5 А В

D

1 С E

х

0 2 5

 

Черт.43.

 

Требуется найти площадь фигуры АВОС.

Вычисляются координаты точек пересечения А, В:

y = x, y = x ² +1,

y = 5, ® В (5; 5). y = 5, ® А (2; 5).

Так как граница фигуры неоднородная, то фигура АВОС разбивается на две части ОСАD и DAB. Площадь первой части равна:

Площадь второй части равна:

Площадь всей фигуры АВОС равна 8/3 + 4,5 » 7,167.

Пример 12. Вычислить площадь фигуры, ограниченной линиями

y = x ², х×y = 8, y = 9.

Решение. y = x ² – это уравнение параболы с вершиной 0(0; 0);

х×y = 8 - это уравнение гиперболы, y = 9 - уравнение прямой, параллельной оси О х. По­лучается фигура АВС (см. черт.44).

у А В

9 у = 9

 

 

4 С

 

x=Ö ` y x= 8/ y

 

0 2 3 х

Черт. 44.

 

Применяется вторая формула для вычисления площадей. Переменная у считается не­зависимой, она принимает значения от у_С до 9. Вычисляются координаты точки С (х _С; у_С):

y = x ²,

х×y = 8, ® С (2; 4).

Тогда 4 £ y £ 9.Границы фигуры АВС выражаются как функции от у: х = 8/ у - левая граница СА, х = Ö ` у - правая граница СВ. Тогда

3. Рассматривается плоская фигура, ограниченная кривыми y = f (x), y = g (x) и прямыми x = a, x = b (при этом 0 £ f (x) < g (x), a < b). Эта фигура вращается вокруг оси Ох, тогда объем V тела, ограниченного поверхностью вращения вычисляется по формуле:

4. Рассматривается плоская фигура, ограниченная кривыми x = F (y),

x = G (y) и прямыми y = c, y = d (при этом 0 £ F (y) < G (y), c < d). Эта фи­гура вращается вокруг оси О у, тогда объем V тела, ограниченного поверхно­стью вращения вычисляется по формуле:

Пример 13. Вычислить объем тела, образованного вращением вокруг оси OY фигуры, ограниченной линиями: y = x ² +1, y = x, y = 5, x = 0.

Решение. Рассматривается фигура АВОС на чертеже 43 из примера 11. Она разбивается на части АВЕС и СЕО, и вычисляются объемы тел, об­разованных вращением этих частей.

Для первого тела границы АВЕС представляются в виде: х = Ö `(у -1), х = у, 1£ у £ 5. Тогда объем V ₁ первого тела равен:

Для второго тела границы СЕО имеют вид: х = у, х = 0, 0£ у £ 1. Тогда объем V ₂ второго тела равен:

Объем всего тела вращения равен »104,720 + 1,047 = 105,767.

Несобственные интегралы

В определении определенного интеграла предполагается, что подын­тегральная функция f (x) ограниченна на [ a; b ], и промежуток [ a; b ] конечен. В данном пункте вводятся несобственные интегралы, для которых ог­раничение конечности промежутка снимается.

Определение 4. Несобственными интегралами с бесконечными пределами интегрирования называются интегралы, определяемые следующим образом:

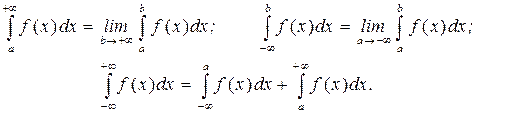Второй вид несобственных интегралов – это интегралы от неограниченных функций. Пусть функция f (x) непрерывна на [ a; b ] кроме точки с Î[ a; b ], в которой f (x) имеет разрывII рода. Тогда несобственный интеграл интеграл от f (x) в пределах от а до b определяется, как сумма следующих пределов:

Если при вычислении несобственного интеграла полу­чаемый предел конечен, то говорят, что несобственный интеграл схо­дится, если нет, то - расходится.

Пример 14. Вычислить следующие несобственные интегралы.

Иногда не требуется вычислять данный несобственный интеграл, а достаточно только выяснить его сходимость. В таких случаях часто сходи­мость несобственного интеграла устанавливается методом сравнения, кото­рый опирается на следующее утверждение.

 

Упражнения

Найти следующие интегралы.

1). ò(x ⁴ - 3 x ³ + 2 x) dx. 2). ò(x - 3 x ²)(2 – x) dx. 3). ò(2 x - 3 x ^1/2 + 4 x ^1/3 – 5/ x) dx.

 

4). 5). 6).

 

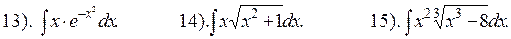10). ò(3 - 2 х)⁴ dx. 11). ò(е^х + е^-х)² dx. 12). ò Ö `(1- 4 х) dx.

 

16). ò х ln (x -1) dх. 17). ò х ×е^{4 х} dх. 18). ò Ö ` х × lnx dx.

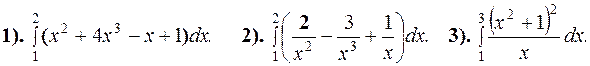1. Вычислить определенные интегралы:

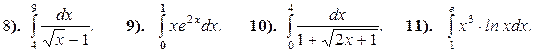
2. Вычислить площадь, ограниченную линиями:

1). y = 0 и y = 9 – x ². 2). y = 0 и y = 3 – 2 x – x ².

3). y = x ² и y = 2 – x ². 4). xy = 6 и x + y = 7.

5). x = 0 и y ² = 2 x + 4. 6). y ² = x ³, y = 8, x = 0.

7). y = 2 ^x , y = 2, x = 0. 8). y = e^x, y = e^-x, x = 1.

3. Определить объем тела, образованного вращением вокруг оси Ох или Оу фигуры, ограниченной указанными линиями:

1). y ² = 4 x, x = 5 вокруг Ох. 2). хy = 4, x = 1, x = 4, у = 0 вокруг Ох.

3). y ² = 4 - x, x = 0 вокруг Оy. 4). y = x ³, x = 0, у = 8 вокруг Оy.

<

Поделиться: