МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ЭКОНОМИКИ, СТАТИСТИКИ И ИНФОРМАТИКИ
Кафедра математической статистики и прогнозирования
Контрольная работа по многомерным статистическим методам
Исполнитель: Елькина НГ, ДЭТ-201
Руководитель: проф., д.э.н Архипова М.Ю.
Москва, 2012
Содержание
Введение………………………………………...…………………………………..3
1. Предварительный анализ данных………………………………………………3
2. Корреляционный анализ………………………………………….....................18
3. Регрессионный анализ……..…………………………………………………..26
4. Факторный анализ……………………………………………………………...31
Заключение ……..………………............................................................................35
Введение
Численность занятого населения оказывает большое влияние на экономику страны. Цель данной работы заключается в выявлении зависимости этого показатели. Чем больше численность занятого населения, тем меньше уровень безработицы и меньше численность людей, находящихся на обеспечении государством, тем больше налогов поступает в бюджет. Высокий уровень безработицы характеризует экономику как неэффективную. По результатам исследования можно будет определить, что влияет на численность занятых. Данные по итогам Всероссийской переписи населения 2010 года взяты с сайта Росстата www.gks.ru. Также Росстат один раз в два года публикует статистический сборник «Труд и занятость в России», и периодически выходит в свет статистический сборник «Экономически активное население». Вопрос о численности занятого населения поднимался во многих работах, например: «Информационная асимметрия на рынке труда» Ведерниковой Н.И., «Современная микроэкономика: анализ и применение» Хаймана Д. Н.
Предварительный анализ данных
С целью анализа взаимосвязей показателей численности занятого населения были рассмотрены показатели населения РФ по регионам. Экономический показатели:
результативный признак:
Y1- население с источником средств к существованию – трудовая деятельность (на 1000 человек населения, указавших источники средств к существованию),
Y2 – работающие по найму в возрасте 15-72 лет на 1000 занятых;
факторные признаки:
X1 – численность населения в регионе,
X2 – медианный возраст,
X3 – число частных домохозяйств;
X4 – население с высшим профессиональным образованием, на 1000 человек в возрасте 15 лет и более.
Исходные данные представлены в таблице 1.Предположим, что рассматриваемые признаки подчиняются нормальному закону распределения.
Таблица 1
Исходные данные
| Субъекты РФ | X1 | X2 | X3 | X4 | Y1 | Y2 |
| А | ||||||
| Белгородская область | 39,8 | |||||
| Брянская область | 39,9 | |||||
| Владимирская область | 41,0 | |||||
| Воронежская область | 41,4 | |||||
| Ивановская область | 40,8 | |||||
| Калужская область | 40,7 | |||||
| Костромская область | 40,5 | |||||
| Курская область | 41,7 | |||||
| Липецкая область | 40,7 | |||||
| Московская область | 39,4 | |||||
| Орловская область | 41,2 | |||||
| Рязанская область | 42,0 | |||||
| Смоленская область | 40,8 | |||||
| Тамбовская область | 42,3 | |||||
| Тверская область | 41,6 | |||||
| Тульская область | 42,2 | |||||
| Ярославская область | 41,0 | |||||
| г. Москва | 39,7 | |||||
| Республика Карелия | 39,2 | |||||
| Республика Коми | 36,6 | |||||
| Архангельская область | 38,0 | |||||
| Ненецкий автономный округ | 33,1 | |||||
| Вологодская область | 38,8 | |||||
| Калининградская область | 38,1 | |||||
| Ленинградская область | 40,3 | |||||
| Мурманская область | 37,0 | |||||
| Новгородская область | 41,2 | |||||
| Псковская область | 41,7 | |||||
| г. Санкт-Петербург | 40,4 | |||||
| Республика Адыгея | 38,0 | |||||
| Республика Калмыкия | 34,0 | |||||
| Краснодарский край | 38,6 | |||||
| Астраханская область | 36,7 | |||||
| Волгоградская область | 38,9 | |||||
| Ростовская область | 39,1 | |||||
| Республика Дагестан | 27,3 | |||||
| Республика Ингушетия | 25,1 | |||||
| Кабардино-Балкарская Республ | 32,8 | |||||
| Карачаево-Черкесская Республ | 34,1 | |||||
| Респуб Северная Осетия-Алания | 35,4 | |||||
| Чеченская Республика | 24,1 | |||||
| Ставропольский край | 36,2 | |||||
| Республика Башкортостан | 36,9 | |||||
| Республика Марий Эл | 37,8 | |||||
| Республика Мордовия | 40,3 | |||||
| Республика Татарстан | 37,6 | |||||
| Удмуртская Республика | 37,1 | |||||
| Чувашская Республика | 38,0 | |||||
| Пермский край | 37,4 | |||||
| Кировская область | 40,8 | |||||
| Нижегородская область | 40,2 | |||||
| Оренбургская область | 37,7 | |||||
| Пензенская область | 41,2 | |||||
| Самарская область | 39,2 | |||||
| Саратовская область | 39,7 | |||||
| Ульяновская область | 41,0 | |||||
| Курганская область | 40,1 | |||||
| Свердловская область | 38,1 | |||||
| Тюменская область | 33,9 | |||||
| Ханты-Мансийский ав окр Югра | 33,3 | |||||
| Ямало-Ненецкий автоном округ | 32,8 | |||||
| Челябинская область | 37,8 | |||||
| Республика Алтай | 32,0 | |||||
| Республика Бурятия | 32,7 | |||||
| Республика Тыва | 27,0 | |||||
| Республика Хакасия | 35,5 | |||||
| Алтайский край | 38,5 | |||||
| Забайкальский край | 32,9 | |||||
| Красноярский край | 36,2 | |||||
| Иркутская область | 35,2 | |||||
| Кемеровская область | 37,3 | |||||
| Новосибирская область | 37,8 | |||||
| Омская область | 37,5 | |||||
| Томская область | 35,3 | |||||
| Республика Саха (Якутия) | 31,2 | |||||
| Камчатский край | 36,1 | |||||
| Приморский край | 37,5 | |||||
| Хабаровский край | 36,3 | |||||
| Амурская область | 35,7 |
X1min=42090 человек проживает в Ненецком автономном округе
X1max=11503501 человек проживает в городе Москве
X2min=24,1 медианный возраст в Чеченской республике
X2max=42,3 медианный возраст в Тамбовской области
X3min=15627 число частных домохозяйств в Ненецком автономном округе
X3max=4416087 число частых домохозяйств в г. Москве
X4min=115 человек с высшим профессиональным образованием, на 1000 человек в возрасте 15 лет и более в Чеченской республике
X4max=410 – в г. Москве
Y1min=183 человека с источником средств к существованию – трудовая деятельность на 1000 человек населения, указавших источники средств к существованию, в республике Ингушетия
Y1max=592 – в Чукотском автономном округе
Y2min=783 человека работают по найму в возрасте 15-72 лет на 1000 занятых
Y2max=970 – в Чукотском автономном округе
Me(X1)=1227626
Me(X2)=37,8
Me(X3)=472478
Me(X4)=198
Me(Y1)=472
Me(Y2)=939
Mo(X2)1=37,1
Mo(X2)2=37,8
Mo(X2)3=38,0
Mo(X2)4=40,8
Mo(X2)5=41,0
Mo(X2)6=41,2
Mo(X4)1=181
Mo(Y1)1=491
Mo(Y2)1=941
Таблица 2
Интервальный ряд распределения
| Интервалы X1 | Частота X1 | Интервалы X2 | Частота X2 | Интервалы X3 | Частота X3 |
| 0-1554081 | 22,9-25,3 | 0-596669 | |||
| 1554081-3108163 | 25,3-27,8 | 596669-1193339 | |||
| 3108163-4662244 | 27,8-30,3 | 1193339-1790008 | |||
| 4662244-6216325 | 30,3-32,7 | 1790008-2386677 | |||
| 6216325-7770407 | 32,7-35,2 | 2386677-2983347 | |||
| 7770407-9324488 | 35,2-37,7 | 2983347-3580016 | |||
| 9324488-10878569 | 37,7-40,1 | 3580016-4176685 | |||
| 10878569-12432651 | 40,1-42,6 | 4176685-4773355 | |||
| Интервалы X4 | Частота X4 | Интервалы Y1 | Частота Y1 | Интервалы Y2 | Частота Y2 |
| 95-135 | 155-211 | 770-796 | |||
| 135-175 | 211-266 | 796-821 | |||
| 175-215 | 266-322 | 821-846 | |||
| 215-255 | 322-377 | 846-872 | |||
| 255-295 | 377-433 | 872-897 | |||
| 295-335 | 433-488 | 897-922 | |||
| 335-375 | 488-543 | 922-948 | |||
| 375-415 | 543-599 | 948-973 |
x̅= 
– средняя арифметическая, где l – число интервалов, n=∑mi – число наблюдений.
x̅1=1675786,4
x̅2=37,5
x̅3=650585,14
x̅4=205,6
y̅1=469,68
y̅2=926,4
Если исходить из построенных интервальных рядов, то медиану следует вычислять по формуле:
где aMe – нижняя граница медианного интервала; mMe – частота встречаемости признака в медианном интервале; mн(Me-1) – накопленная частота интервала, предшествующего медианному.
M̂e1=1151685
M̂e2=38,1
M̂e3=450214
M̂e4=200
M̂e5=472,1
M̂e6=934,9
Qниж=xQ1+h* 
Qверх= xQ3+h* 
,
где xQ1 – нижняя граница интервала, содержащего нижний квартиль; xQ3 – нижняя граница интервала, содержащего верхний квартиль; SQ1-1 – накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль; SQ3-1 – то же, для верхнего квартиля; fQ1 – частота интервала, содержащего нижний квартиль; fQ2 – то же, для верхнего квартиля.
Qниж(X1)=575842,5
Qверх(X1)=2201615,2
Qниж(X2)=35,6
Qверх(X2)= 40,3
Qниж(X3)=225106,9
Qверх(X3)=867035,1
Qниж(X4)=182,4
Qверх(X4)=221,8
Qниж(Y1)=442,5
Qверх(Y1)=513,4
Qниж(Y2)=925,25
Qверх(Y2)=945,23
Для одномодального интервального ряда вычисление моды можно производить по формуле:
где aMо – нижняя граница модального интервала; mMо – частота встречаемости признака в модальном интервале; m(Mо-1) – частота интервала, предшествующего модальному; m(Mо+1) – частота интервала, следующего за модальным.
M̂0(X1)=897201,4021
M̂0(X2)=40,378
M̂0(X3)=349114,84
M̂0(X4)=192,5
M̂0(Y1)=466,673
M̂0(Y2)=936,209
Выборочная дисперсия и среднее квадратическое отклонение характеризуют степень разброса или рассеяния значений случайной величины вокруг её среднего значения. Выборочная дисперсия S2 равна центральному моменту второго порядка:
S2(X1)=2975050664884,23
S2(X2)=14,814
S2(X3)=437821706458,6
S2(X4)=1661,08
S2(Y1)=4787,768
S2(Y2)=2172,4
S(X1)= 1724833,518
S(X2)= 3,8489
S(X3)= 661680,9703
S(X4)= 40,756
S(Y1)= 69,1937
S(Y2)= 46,609
Размах варьирования признака рассчитывается по формуле R=xmax - xmin
R(X1)= 11461411
R(X2)= 18,2
R(X3)= 4400460
R(X4)= 295
R(Y1)= 409
R(Y2)= 187
Коэффициент эксцесса Ek – показатель, служащий мерой крутости (плосковершинности или островершинности) графика вариационного ряда в сравнении с кривой нормального распределения. Определяется Ek по формуле: 
Ek(X1)=12,45
Ek(X2)=2,65227
Ek(X3)=12,3684
Ek(X4)=6,2965
Ek(Y1)=3,8455
Ek(Y2)=-1,547
Если Ek>0, то график ряда распределения является островершинным, если Ek<0 – плосковершинным по сравнению с нормальным.
Коэффициент асимметрии Ac – показатель асимметричности распределения, определяющий степень скошенности кривой по сравнению с нормальным распределением. Вычисляется Ас по формуле: 
Ac(X1)=3,054
Ac(X2)=-1,47
Ac(X3)=3,03
Ac(X4)=1,8446
Ac(Y1)=-1,405
Ac(Y2)=-0,4746
Для симметричных вариационных рядов Ас=0, в случае правосторонней асимметрии Ас>0, при левосторонней Ас<0. Если |Ac|>0,5, то асимметрия существенна.
Выборочная медиана для X1 больше выборочного среднего и находится между нижним и верхним квартилями. Выборочная медиана для X2 больше среднего, но незначительно и, как в первом случае, расположена между нижним и верхним квартилями. Выборочная медиана для X3 значительно меньше среднего и находится между верхним и нижним квартилями. Выборочная медиана для X4 меньше среднего и располагается между квартилями. Выборочная медиана Y1 больше среднего и находится между квартилями. Выборочная медиана Y2 больше среднего, расположена между верхним и нижним квартилями.
Для визуального подбора теоретического распределения, а также выявления положения среднего значения и характера рассеивания вариационные ряды изображают графически. Гистограмма отражает распределение значений изучаемого признака по интервалам и представляет собой эмпирический аналог функции плотности вероятностей.
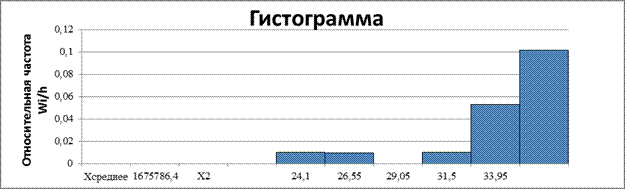
Рис. 1. Гистограмма относительных частот интервального ряда распределения Х1
Гистограмма является аппроксимацией кривой плотности вероятности f(x) теоретического распределения генеральной совокупности. Поэтому по её виду можно судить о гипотетическом законе распределения.
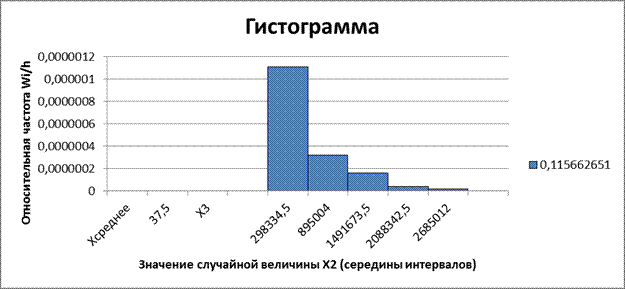
Рис. 2. Гистограмма относительных частот интервального ряда распределения Х2
Рис. 3. Гистограмма относительных частот интервального ряда распределения Х3
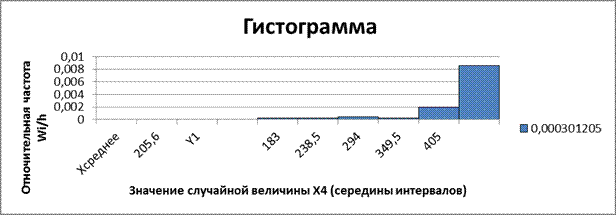
Рис. 4. Гистограмма относительных частот интервального ряда распределения Х4
Рис. 5. Гистограмма относительных частот интервального ряда распределения Y1
Рис. 6. Гистограмма относительных частот интервального ряда распределения Y2
Кумулятивная кривая (кумулята) – кривая накопленных частот (частостей). С кумулятой сопоставляется график интегральной функции распределения F(x).
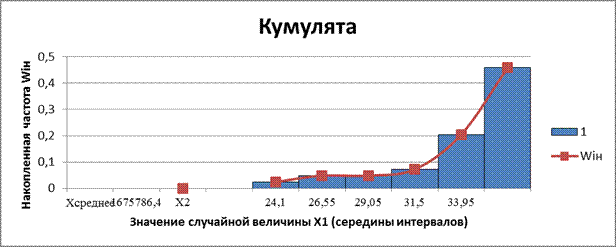
Рис. 7. Кумулята накопленных частот интервального ряда распределения X1
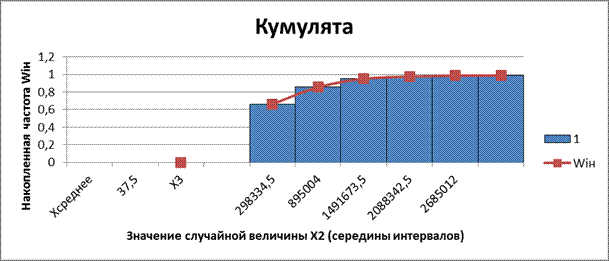
Рис. 8. Кумулята накопленных частот интервального ряда распределения X2
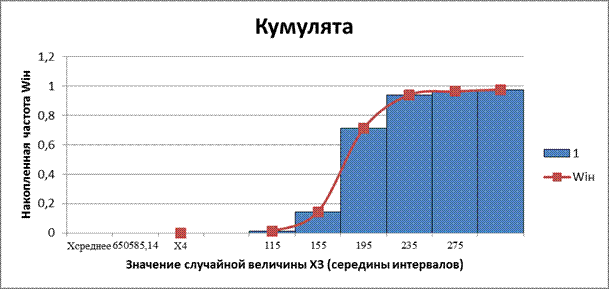
Рис. 9. Кумулята накопленных частот интервального ряда распределения X3
Рис. 10. Кумулята накопленных частот интервального ряда распределения X4
Рис. 11. Кумулята накопленных частот интервального ряда распределения Y1
Рис. 12. Кумулята накопленных частот интервального ряда распределения Y2
По правилу трёх сигм 3σ практически все значения нормально распределённой случайной величины лежат в интервале [x̅ - 3σ; x̅ + 3σ] и не менее чем с 99,7% достоверностью значение нормально распределённой случайной величины лежит в указанном интервале. Мы используем выборочное среднее квадратичное отклонение, поэтому правило трёх сигм преобразуется в правило 3S. Для Х1 два значения лежат выше данной границы. Для Х2 два значения – ниже данного интервала. Для Х3 два значения выходят за верхнюю границу интервала. Для Х4 два значения находятся выше правой границы. Для Y1 два значения ниже интервала. Для Y2 одно значение ниже границ интервала [x̅ - 3σ; x̅ + 3σ].
Появление резко выделяющихся наблюдений может быть вызвано прямой ошибкой или существенным искажением стандартных условий сбора статистических данных, при котором однородность выборки была нарушена. Известен ряд методов отсева грубых погрешностей.
Критерий Смирнова-Граббса
Этот критерий основа на вычислении максимального относительного отклонения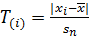 
, где хi – крайний (минимальный x(1) или максимальный x(n)) элемент вариационного ряда, ̅х – среднее по выборе, sn – выборочное среднее квадратическое отклонение. Значения Т(1) и Т(n) сравнивают с критическими значением Сα метода Смирнова-Граббса. Выборка не содержит грубых погрешностей, если Т(i)≤ Сα, i=1,n. Наблюдения делят на три группы в зависимости от вычисленных относительных отклонений Т(i), i=1,n; n:
1) Т(i)≤ С10% - наблюдение не нарушает однородность выборки и не отсеивается;
2) Т(i) > С2,5% - наблюдение значимо отклоняется от ̅х, является грубой погрешностью и отсеивается как нетипичное;
3) С10% <Т(i)≤ С2.5% - требуются дополнительные аргументы в пользу отсева наблюдения.
Такими аргументами могут служить соображения эксперта-оценщика, связанные с методологией получения данных для выборки, или существенный выигрыш в снижении ошибки оценки – среднеквадратическое отклонение с учетом «штрафа за уменьшение объема выборки», выражающейся в ширине доверительного интервала. В случае сомнений целесообразно проверить наблюдение с помощью других критериев и сравнить полученные результаты.
Критерий Граббса
Критерий Граббса основан на сравнении сумм квадратов отклонений от среднего исходной и сокращённой (без крайнего элемента) выборок. По вариационному ряду получают оценки ̅х1 и х 1, где 
- среднее по выборке без x(n), 
- среднее без x(1), и проверяют критерий G1 для минимального x(1) и Gn для максимального x(n) значений ряда:
; 
.
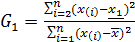Если значения статистик G1 и Gn окажутся меньше критического значения Сα’, то соответствующие наблюдения х1 или хn относят к грубым ошибкам. После отсева наблюдений, признанных нетипичными, проверку на грубые ошибки повторяют для сокращенной выборки.
Оба рассмотренных критерия применимы для проверки на аномальность единичных наблюдений (минимального или максимального), однако в ситуации, когда выборка содержит группу близких по значениям аномальных наблюдений, они могут не дать результата. В этом случае можно использовать критерий Титьена-Мура, являющийся обобщением критерия Граббса на несколько наблюдений.
Критерий Титьена-Мура
Для k максимальных наблюдений выборки проверяется статистика
, 
.
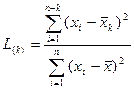Модификация критерия Граббса для k минимальных значений выборки проводится аналогичным образом:
; 
.
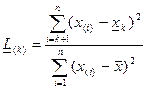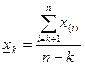Если значения статистик окажутся меньше критического значения, то соответствующие наблюдения исключаю, так как они считаются грубыми ошибками.
В исходных данных вызывают сомнения значения для X1 42090, 50526, 11503501. Для двух минимальных значений получаем 
=0,9751 C0,1%=0,725 C0,5%=0,757 C1%=0,7715 C2,5%=0,7915 C5%=0,3075 C10%=0,8245. На любом уровне значимости значение больше критического, то есть данные минимальные значения не являются выбросами. Значения статистики Gn=0,5954 меньше критических на уровнях значимости C0,1%=4,012 C0,5%=3,687 C1%=3,534 C2,5%=3,319 C5%=3,147, но для C10%=0,295 больше, поэтому не считается выбросом. Для Х2 возможны два выброса 24,1и 25,1. Исключив их, получаем статистику =0,7181. Значение больше только при C5%=0,3075.
Для Х3 за выбросы можно принять 15627, 21417 и 4416087. Вычислим статистику для двух минимальных значений =0,9756. Значение больше критических на всех уровнях значимости, то есть это не выбросы. Для максимального значения статистика равна Gn=0,597, только с вероятностью ошибки 10% значения не считается выбросом.
Для X4 за выбросы можно принять 115 и 410. Тогда G=0,63 и C0,1%=0,7215 C0,5%=0,7488 C1%=0,7614 C2,5%=0,7792 C5%=0,7938 C10%=0,8097. Значение ниже критических на всех уровнях, то есть оба считают за выбросы.
Для Y1 выбросами могут являться 183 и 214. По формуле получаем значение статистики =0,5939, которое меньше критических на всех уровнях, кроме C5%=0,3075, то есть только на этом уровне значимости 5% не являются выбросами.
Для Y2 выбросом может быть 970. Критерий Gn=0,9772, значение которого больше критических на всех уровнях, показывает, что это не выброс.
Другой способ обнаружить выбросы – это ящичковые диаграммы.
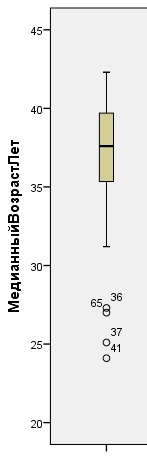
Рис. 13. Ящичковые диаграммы
* - значения, отстоящие от 75%-го процентиля более чем на 3 длины ящичка (экстремумы);
° - значения, отстоящие от 75%-го процентиля более чем на 1,5 длины ящичка (выбросы);
верхний «ус» - наибольшее из наблюденных значений, которое не является ни выбросом, ни экстремумом;
нижний «ус» - наименьшее из наблюденных значений, которое не является ни выбросом, ни экстремумом;
верхний край ящичка – 75% процентиль;
нижний край ящичка – 25% процентиль;
горизонтальная линия в ящичке – медиана.
Таким образом, каждый признак имеет значения, которые являются выбросами. Значения среднего и стандартного отклонения чувствительны к выбросам, и могут значительно меняться при наличии экстремальных значений в ряду данных.
Корреляционный анализ
Парные коэффициенты корреляции характеризуют взаимосвязь между двумя выбранными переменными на фоне действия остальных показателей и являются самыми распространёнными показателями тесноты связи при статистическом анализе изучаемых данных.
Для значимых парных коэффициентов корреляции можно построить с заданной надёжностью γ =0,95 интервальную оценку ρmin ≤ ρ ≤ ρmax.
P(0,006628≤ ρY1X1 ≤ 0,417689)=0,95
P(0,015058≤ ρY2X4 ≤ 0,424624)=0,95
P(0,034138≤ ρХ2X3 ≤ 0,440145)=0,95
По полученным данным можно сделать следующие выводы. Между исследуемыми показателями выявлены значимые корреляционные зависимости:
Ø Значимые корреляционные прямые взаимосвязи обнаружены между изучаемым признаком Y1 – население с источником средств к существованию - трудовая деятельность (на 1000 чел населения, указавших источники средств к существованию) и факторным признаком X1 – численностью населения; между Y2 - работающие по найму в возрасте 15-72 лет на 1000 занятых и X4 – население с высшим профессиональным образованием, на 1000 чел в возрасте 15 лет и более; и X2 – медианным возрастом и Х3 – числом частным домохозяйств.
Ø Наиболее сильная связь существует между Х2 и Х3, но она считается слабой.
Частные коэффициенты корреляции характеризуют взаимосвязь между двумя выбранными переменными при исключении влияния остальных показателей и важны для понимания взаимодействия всего комплекса показателей, так как позволяют определить механизмы усиления-ослабления влияния переменных друг на друга.
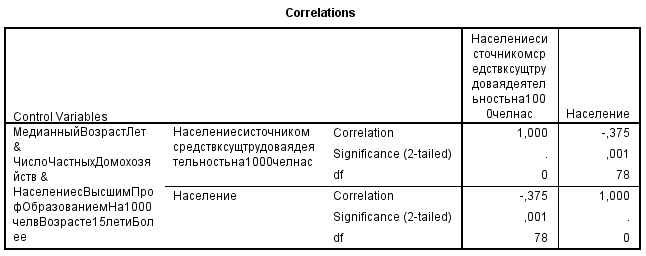
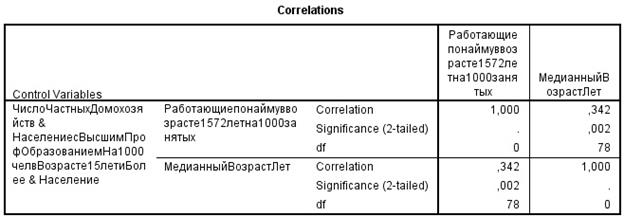
По результатам расчёта значение t-статистики для частных коэффициентов корреляции можно сделать вывод о значимости частных коэффициентов корреляции 
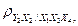
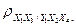
Следовательно, гипотеза о равенстве нулю этих коэффициентов отвергается с вероятностью ошибки, равной 0,05, то есть соответствующие коэффициенты значимы. Для остальных коэффициентов наблюдаемое значение t-статистики меньше критического значения по модулю, то есть гипотеза H0 не отвергается, то есть они незначимы.
Таблица 3
Матрица частных коэффициентов корреляции исследуемых показателей с выделением значимых коэффициентов (при α=0,05)
| X1 | X2 | X3 | X4 | Y1 | |
| X1 | 1,000 | -0,477 | 0,996 | 0,045 | -0,375 |
| X2 | -0,477 | 1,000 | 0,493 | -0,180 | 0,265 |
| X3 | 0,996 | 0,493 | 1,000 | 0,007 | 0,362 |
| X4 | 0,045 | -0,180 | 0,007 | 1,000 | 0,457 |
| Y1 | -0,375 | 0,265 | 0,362 | 0,457 | 1,000 |
| X1 | X2 | X3 | X4 | Y2 | |
| X1 | 1,000 | -0,392 | 0,996 | -0,092 | -0,444 |
| X2 | -0,392 | 1,000 | 0,404 | -0,980 | 0,342 |
| X3 | 0,996 | 0,404 | 1,000 | 0,142 | 0,437 |
| X4 | -0,092 | -0,980 | 0,142 | 1,000 | 0,100 |
| Y2 | -0,444 | 0,342 | 0,437 | 0,100 | 1,000 |
Доверительные интервалы с надёжностью γ= 0,95 для значимых частных генеральных коэффициентов корреляции определяются так же, как и для парных коэффициентов корреляции через Z-преобразование.
Таблица 4
Доверительных интервалов для частных генеральных коэффициентов показателей с надёжностью γ= 0,95
| для Y1 | Y1X1 | Y1X2 | Y1X3 | Y1X4 | X1X2 | X1X3 | X2X3 |
| ρ min | -0,5465 | 0,0523 | 0,1587 | 0,2677 | -0,6281 | 0,9938 | 0,3103 |
| ρmax | -0,1733 | 0,4547 | 0,5358 | 0,6123 | -0,2913 | 0,9974 | 0,6406 |
| дляY2 | Y2X1 | Y2X2 | Y2X3 | Х2X4 | X1X2 | X1X3 | X2X3 |
| ρ min | -0,6020 | 0,1334 | 0,2443 | -0,9871 | -0,5603 | 0,9938 | 0,2063 |
| ρmax | -0,2525 | 0,5194 | 0,5965 | -0,9692 | -0,1926 | 0,9974 | 0,5700 |
Сравнение парных и частных коэффициентов играет важную роль в выявлении механизмов воздействия переменных друг на друга. Парный коэффициент корреляции показывает тесноту связи между двумя признаками на фоне действия остальных переменных, а частный – характеризует взаимосвязь этих двух признаков при исключении влияния остальных переменных. Если парный коэффициент корреляции между двумя переменными по модулю больше соответствующего частного, то остальные переменные усиливают связь между этими двумя признаками. Соответственно, если парный коэффициент корреляции между двумя переменными по абсолютной величине меньше частного, то остальные признаки ослабляют связь между рассматриваемыми двумя. Парный коэффициент корреляции между Х1 и Y1 0,222 меньше частного по модулю |-0,375|, значит признаки X2, X3, X4 уменьшают связь. Так же парная связь для признаков X2 и Х3, меньше частной.
Множественные коэффициенты корреляции служат мерой связи одной переменной с совместным действием всех остальных показателей. Вычислим точечные оценки множественных коэффициентов корреляции. Множественный коэффициент корреляции, например, для 1-го показателя Y вычисляется по формуле: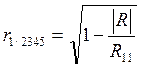 
,где | R | - определитель корреляционной матрицы R; Rii – алгебраическое дополнение элемента rii корреляционной матрицы R.
Таблица 5
Множественные коэффициенты корреляции
| Для Y1 | Для Y2 | |
| rY/{…} | 0,746152 | 0,747891 |
| rX1/{…} | 0,997716 | 0,997918 |
| rX2/{…} | 0,712124 | 0,724909 |
| rX3/{…} | 0,997802 | 0,998005 |
| rX4/{…} | 0,707213 | 0,61244 |
Самая тесная связь наблюдается между X1 – численностью населения и другими показателями. Наименьшей является связь между X4 – численностью населения с высшим профессиональным образованием и остальными признаками, хотя и эта связь >0,5, то есть средняя.
Множественный коэффициент детерминации R2i/{..} (и его выборочная оценка r2i/{..}) показывает долю дисперсии рассматриваемой случайной величины, обусловленную влиянием остальных переменных, включённых в корреляционную модель.
Соответственно (1- R2i/{..}) показывает долю остаточной дисперсии данной случайной величины, обусловленную влиянием других, не включённых в исследуемую модель факторов.
Множественные коэффициенты детерминации получаются возведением соответствующих множественных коэффициентов корреляции в квадрат.
Таблица 6
Множественные коэффициен