ЛАБОРАТОРНАЯ РАБОТА 7
Моделирование параметрических временных рядов
Цель работы: ознакомить студентов с параметрическими временными рядами.
Основные теоретические сведения
1.1 Авторегрессионные (AutoRegression) модели порядка р - AR(p) - определяются следующим образом:
(1)
В выражении (1) величины 
1,..., р используются для обозначения набора весовых коэффициентов; at определяет белый шум, т.е. at ~ WN (0,σ a 2).
В равенстве (1) переменная Хt регрессирует на свои предшествующие значения, поэтому модель называется авторегрессионной. Следовательно, авторегрессионный процесс можно охарактеризовать как модель, в которой текущее значение ряда в момент t выражается через конечное число прошлых значений (систематическая зависимость от прошлых значений) и величину возмущения at, не зависящую от прошлого.
Для изучения свойств временного ряда (ВР) удобно ввести оператор сдвига назад, равный 
, т.е. действие этого оператора на ВР дает значение ряда в предыдущий момент времени. Последовательное применение оператора сдвига р раз определяет значение ВР в момент времени на р периодов ранее, что позволяет ввести степень сдвига оператора 
С помощью оператора сдвига модель (1) можно записать в эквивалентной форме
которая после введения оператора авторегрессии 
принимает вид
Формально процесс AR (p) можно представить как прошедший через фильтр белый шум. Передаточная функция такого фильтра определяется как
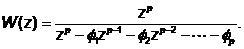
Соответствующее характеристическое уравнение имеет вид
zp – 1 zp-1 - 2 zp-2 - …- p = 0. (2)
В случае, если все р корней уравнения (2) находятся внутри окружности единичного радиуса (все корни по модулю меньше единицы), то процесс AR (p) является стационарным.
Автокорреляции удовлетворяют соотношению:
Из выражения (1) получаем для процесса AR (1) уравнение в виде
Xt = 1 Xt - 1 + at. (3)
Для автокорреляционной функции (АКФ) процесса AR (1) имеем
ρ h = 1 h для h > 0. (4)
1.2 Модель скользящего среднего (Moving Average) порядка q - MA ( q) определяется как
(5)
где символы q1,..., qq используются для обозначения конечного набора весовых параметров.
Эта модель предполагает, что в ошибках модели в предшествующие периоды сосредоточена информация по всей предистории ряда.
Соотношение (5) определяет процессМА (q), который представляет собой линейную комбинацию текущего и прошлых значений шума at.
Используя оператор сдвига назад В, можно записать для процесса (5) эквивалентное выражение
(6)
Из равенства (6) следует, что процесс скользящего среднего можно трактовать как выход Хt линейного фильтра с передаточной функцией q(B), на вход которого поступает белый шум at. Как видно из соотношения (5), процесс Хt при любом n ≥ q определяется конечным числом значений at, аt – 1 ,..., аt – q белого шума, поэтому такой фильтр принято называть фильтрами с конечной памятью. При n ≥ q процесс является стационарным со средним значением E { Хt } = 0.
Для АКФ следует очевидное представление
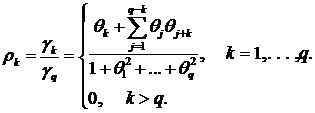
Таким образом, для модели МА(q) автокорреляция обрывается на задержке q, и конечная протяженность автокорреляции является характерным свойством этой модели. В этой модели статистическая связь между наблюдениями сохраняется в течение q единиц времени (т.е. протяженность памяти процесса равна q).
Полученный результат принципиально различает процессы AR(р) и МА(q): если у процесса AR(р) при τ → ∞ (монотонно или колебательно) АКФ постепенно стремится к нулю, то у процесса МА(q) при τ = q АКФ обрывается и в последующем остается равной нулю.
Для модели МА(1) из (5) получаем
Xt = at + θ1 аt – 1. (7)
Для АКФ элементарные преобразования дают
ρ0 = 1; ρ1 = θ1 / (1 + θ12), ρ l = 0 для l > 1. (8)
Таким образом, для модели МА(1) при лаге, равном 1, АКФ не равна нулю, но для больших значений лагов АКФ обращается в нуль. М Можно сказать, что АКФ модели МА(1) обрывается на лаге, равном 1, т.е. модель МА(1) не "помнит", что произошло в момент, соответствующий двум временным интервалам назад!
1.3 Смешанные модели АRMA (р,q)
Моделями АR (р) и МА (q) за счет выбора их порядков р и q можно удовлетворительно описывать многие реальные процессы. Однако на практике такие процессы становятся чересчур громоздкими из-за необходимости применения моделей высокого порядка для адекватного описания динамической структуры данных. Для достижения большей гибкости в подгонке моделей к наблюдаемым ВР иногда бывает целесообразным объединить в одной модели и авторегрессию, и скользящее среднее. Решению этой задачи помогает рассмотрение смешанных моделей авторегрессии - скользящего среднего, т.е. моделей АRMA (р,q), которые имеют следующий вид
Xt = 1 Xt -1 + …+ p Xt -p + at + θ1 аt – 1 +…+ θ q аt – q (9)
или в другой эквивалентной форме через операторы
(В) Xt = θ(В) at, (10)
где (B), q (B) - операторы, определенные ранее для моделей АR (р) и МА (q); - оператор сдвига назад.
Используя выражение (10), можно сделать следующие выводы:
· ВР { Xt } является AR-процессом порядка р, т.е. AR(р), если θ(В)= 1 или (В) Xt = et, где et подчиняется процессу скользящего среднего порядка q, т.е. et = θ(В) at;
· ВР { Xt } является МА-процессом порядка q, т.е. MA(q), если (В)= 1 или Xt = θ(В) bt, где bt подчиняется процессу авторегрессии порядка р, т.е. (В) bt = at.
Таким образом, (В) Xt = θ(В) (В) bt =θ(В) at.
Очевидно, что члены со скользящим средним в правой части (9) не оказывают влияния на условия стационарности процесса авторегрессии. Вследствие этого выражение (10) является стационарным процессом при условии, что все корни характеристического уравнения (В) = 0 лежат вне единичного круга.
В простейшем случае для модели АRMA (1,1) из (9) имеем
Xt = 1 Xt -1 + at + θ1 аt – 1. (11)
Свойства модели АRMA(1,1) являются обобщением свойств модели АR(1) с некоторыми незначительными изменениями, вызванными воздействием компонента модели MA(1).
АКФ модели АRMA(1,1) с использованием предыдущих результатов определяется следующим образом
ρ1 = 1 + θ1 σa2 / γ 0, ρ h = 1 ρ h – 1 для h > 1, (12)
где γ 0 - дисперсия процесса АRMA (1,1).
Таким образом, АКФ модели АRMA (1,1) ведет себя во многом подобно изменению АКФ модели АR(1) за исключением того, что экспоненциальный спад начинается с лага h = 2, следовательно, АКФ процесса АRMA (1,1) не обрывается на любом конечном лаге.
Идентификация порядка
Методы идентификации, по существу, представляют собой процедуры, которые применяются к данным наблюдений для выявления типа моделей с целью использования последних в дальнейших исследованиях, например, при прогнозировании. Цель идентификации заключается в том, чтобы получить некоторую информацию о конкретных значениях параметров p и q, определяющих вид модели.
Модель авторегрессии
Для определения порядка р модели авторегрессии можно использовать частную автокорреляционную функцию (ЧАКФ). ЧАКФ временного ряда является функцией его АКФ и служит полезным средством для определения порядка модели AR(p). Отметим, что АКФ определяется ковариацией между значениями процесса, отстоящими на τ шагов по времени друг от друга. Однако на поведение процесса AR(p) статистически влияет не только его значение в момент, равный τ шагов назад, но и все промежуточные значения процесса между моментами t и t – τ. ЧАКФ исключает влияние всех промежуточных значений ряда и показывает лишь "чистую" взаимосвязь между моментами t и t – τ.
Для модели AR(p) выборочная ЧАКФ обрывается на лаге р, что и может служить идентификацией порядка этой модели.
Модель скользящего среднего
Автокорреляционная функция является полезной при идентификации порядка рассматриваемой МА-модели. ВР Xt описывается моделью МА(q), если его АКФ ρ q ≠ 0, но значение ρ l = 0 при l > q.
Смешанная модель
В рассмотренных моделях AR(p) и MA(q) вид АКФ и ЧАКФ дает возможность идентифицировать параметры этих процессов. Напомним, что процесс { Xt } описывается моделью MA(q), если соответствующая АКФ срезается до нуля на лаге q. С другой стороны, ЧАКФ процесса { Xt } обрывается на лаге р при описании последнего моделью AR(p).
Процесс ARMA(p,q) объединяет свойства моделей AR(p) и MA(q), поэтому у процесса ARMA(p,q) при лагах τ > q действие его компонента в виде скользящего среднего прекращается и оказывает влияние только авторегрессионная составляющая. Вследствие этого при τ > q поведение АКФ процесса ARMA(p,q) аналогично характеру изменений АКФ процесса AR(p), т.е. с увеличением лага постепенно стремится к нулю.
С другой стороны, рассмотрение частных автокорреляций приводит к следующему: в связи с тем, что ЧАКФ процесса AR(p) становится равной нулю при лагах τ > р, то на поведение ЧАКФ процесса ARMA(p,q) при τ > р влияет его составляющая в виде MA(q). В итоге, это приводит к тому, что ЧАКФ процесса ARMA(p,q) постепенно сходится к нулю.
Было установлено, что АКФ такого процесса, содержащая компонент авторегрессии порядка р и составляющую скользящего среднего порядка q, после первых (q – р) задержек представляется в виде суммы экспонент и затухающих синусоид. С другой стороны, ЧАКФ этой модели приближенно описывается суммой экспонент и затухающих синусоид после (p – q). Однако для смешанной модели АКФ и ЧАКФ не дают достаточной информации с точки зрения нахождения параметров р и q. В частности, визуальный анализ графиков АКФ и ЧАКФ не позволяет однозначно определить параметры р и q модели ARMA(p,q).
Работа на компьютере