Практическая ценность математико-статистических методов во многом зависит от того, насколько быстро, качественно и с какими затратами они позволяют получать желаемый результат.
Данная методика позволяет формализовать процедуру построения классификационных шкал для пользователей, не имеющих глубоких знаний в области специальных статистических методов обработки данных, в том числе при малом объеме исходных данных.
Шаг 1. Для заданных исходных данных {  } объема N рассчитываются значения математического ожидания
} объема N рассчитываются значения математического ожидания
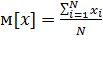 (3.5)
(3.5)
и среднеквадратического отклонения
 (3.6)
(3.6)
Расчет значения формы распределения
 (3.7)
(3.7)
Шаг 2. Считая число классов состояния заданным заранее, определяются параметры законов распределения случайных величин внутри классов состояний на основе соотношений и таблиц, приведенных ниже.
Для случая двух классов зависимости имеют вид:
Зависимость параметров формы законов распределения внутри классов от параметра формы исходного распределения:


Зависимость среднеквадратического отклонения случайных величин внутри классов состояния от среднеквадратического отклонения исходных данных при различных значениях параметра формы исходного закона распределения:
Таблица 3.6 – Зависимости характеристик законов распределения для двух классов состояния
| Значение параметра формы исходного распределения | Значение среднеквадратического отклонения случайной величины внутри первого класса состояния | Значение среднеквадратического отклонения случайной величины внутри второго класса состояния |
 =1 =1
| 
| 
|
 =1,5 =1,5
| 
| 
|
 =2 =2
| 
| 
|
 =2,5 =2,5
| 
| 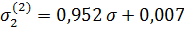
|
 =3 =3
| 
| 
|
 =3,5 =3,5
| 
| 
|
 =4 =4
| 
| 
|
 =4,5 =4,5
| 
| 
|
Учитывая то, что графически данные зависимости представляют собой набор прямых линий (рисунок 3.17), расстояние между которыми уменьшается с ростом значения  , и наиболее существенное различие между прямыми, соответствующими
, и наиболее существенное различие между прямыми, соответствующими  =4 и
=4 и  =4,5 не превышает 5%, целесообразно при
=4,5 не превышает 5%, целесообразно при  >4,5 пользоваться зависимостями, представленными для
>4,5 пользоваться зависимостями, представленными для  =4,5.
=4,5.


Рисунок 3.17 – Зависимости характеристик законов распределения для первого из двух класса состояния
Для случая трех классов зависимости имеют вид:
Зависимость параметров формы законов распределения внутри классов от параметра формы исходного распределения:



Зависимость среднеквадратического отклонения случайных величин внутри классов состояния от среднеквадратического отклонения исходных данных при различных значениях параметра формы исходного закона распределения:
Таблица 3.7 – Зависимости характеристик законов распределения для трех классов состояния
| Значение параметра формы исходного распределения | Значение среднеквадратического отклонения случайной величины внутри первого класса состояния | Значение среднеквадратического отклонения случайной величины внутри второго класса состояния |
 =1 =1
| 
| 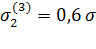
|
 =1,5 =1,5
| 
| 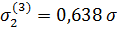
|
 =2 =2
| 
| 
|
 =2,5 =2,5
| 
| 
|
 =3 =3
| 
| 
|
 =3,5 =3,5
| 
| 
|
 =4 =4
| 
| 
|
 =4,5 =4,5
| 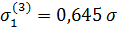
| 
|
Таблица 3.7 – Продолжение
| Значение параметра формы исходного распределения | Значение среднеквадратического отклонения случайной величины внутри третьего класса состояния |
 =1 =1
| 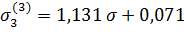
|
 =1,5 =1,5
| 
|
 =2 =2
| 
|
 =2,5 =2,5
| 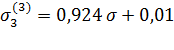
|
 =3 =3
| 
|
 =3,5 =3,5
| 
|
 =4 =4
| 
|
 =4,5 =4,5
| 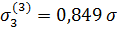
|
Руководствуясь соображениями, приведенными для случая двух классов, для классификации объектов на три класса состояния при значении характеристики формы закона распределения, большей 4,5, следует пользоваться соотношениями, приведенными для  =4,5.
=4,5.
Шаг 3. Выбор модели оценивания закона распределения на основе соотношения
 ,
,
где ДПМ – унифицированная параметрическая модель, получаемая на основе формализма Джейнса,
УПМ –унифицированная параметрическая модель
Унифицированная параметрическая модель приведена в приложении.
Шаг 4. Восстановление законов распределения внутри классов состояния.
Шаг 5. Определение значений оптимальной вероятности β на основе соотношения
 .
.  (3.4)
(3.4)

где  – оптимальное значение вероятности для двух классов,
– оптимальное значение вероятности для двух классов,
 – оптимальное значение вероятности длятрех классов
– оптимальное значение вероятности длятрех классов
 – оптимальное значение вероятности длячетырех классов
– оптимальное значение вероятности длячетырех классов
N – объем выборки.
Шаг 6. Расчет границ классов в соответствии со значением β.
Шаг 7. Определение интервалов группирования. Построение классификационной шкалы с пересекающимися классами.
Пример:
Имеются 20 участков территории  , которым ставится в соответствие значение характеристического признака. Значения признака для каждого участка приведены в таблице 3.9.
, которым ставится в соответствие значение характеристического признака. Значения признака для каждого участка приведены в таблице 3.9.
Таблица 3.9 – Значения характеристического признака

| 
| 
| 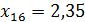
|

| 
| 
| 
|
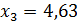
| 
| 
| 
|

| 
| 
| 
|

| 
| 
| 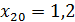
|
Требуется классифицировать участки ТС на 3 класса состояния.
Шаг 1.



Шаг 2. Определение характеристик форм законов распределения внутри классов состояния:



В силу того, что эмпирическое значение  =1,52 не совпадает с приведенными в таблице 2, выбираются наиболее близкие большее и меньшее значения h из таблицы:
=1,52 не совпадает с приведенными в таблице 2, выбираются наиболее близкие большее и меньшее значения h из таблицы:
 =1,5 =1,5
| 
| 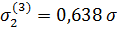
| 
|
 =2 =2
| 
| 
| 
|
Учитывая, что σ=1,34, получаем:
 =1,5 =1,5
| 
| 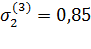
| 
|
 =2 =2
| 
| 
| 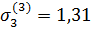
|
Для расчета значений характеристик распределений внутри классов необходимо ввести новые обозначения: пусть  х – расчетное значение характеристики формы распределения,
х – расчетное значение характеристики формы распределения,  1 – наиболее близкое меньшее значение характеристики формы;
1 – наиболее близкое меньшее значение характеристики формы;  2 – наиболее близкое большее значение; σх – расчетное значение характеристики масштаба, σ1 – значение характеристики масштаба, соответствующее
2 – наиболее близкое большее значение; σх – расчетное значение характеристики масштаба, σ1 – значение характеристики масштаба, соответствующее  1, σ2 – значение характеристики масштаба, соответствующее
1, σ2 – значение характеристики масштаба, соответствующее  2. Тогда
2. Тогда
 (3.8)
(3.8)
На основе данной формулы получаем:
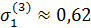 ;
;  ;
;  .
.
Шаг 3. Выбор модели закона распределения случайной величины внутри первого класса состояния: Учитывая, что 0,4 <  < 0,83, для восстановления законов распределения внутри классов состояния необходимо воспользоваться унифицированной параметрической моделью.
< 0,83, для восстановления законов распределения внутри классов состояния необходимо воспользоваться унифицированной параметрической моделью.
Шаг 4. Восстановление закона распределения внутри первого класса состояния: Из таблицы, содержащей модели законов распределения, необходимо выбрать два наиболее близких закона распределения на основе близости значений характеристик формы:
 =s/M[x] =s/M[x]
| Тип закона распределения | Параметры распределения | |
| 0,605 | Вейбулла | α =1,7 | β =1,85 |
| 0,577 | Гамма | α= 3 | β =0,577 |
Восстанавливаются законы распределения на основе унифицированной параметрической модели и для каждого значения абсциссы рассчитывается значение ординаты на основе соотношения (3.8). На рисунке 3.18 представлены графики исходных и восстановленного законов распределения.

Рисунок 3.18 – Восстановление закона распределения внутри первого класса состояния
Для получения закона распределения, соответствующего исходному масштабу, необходимо воспользоваться следующим преобразованием:
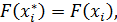 (3.9)
(3.9)
где  .
.
Аналогичным образом восстанавливаются законы распределения случайных величин внутри второго и третьего класса состояния. Восстановленные законы распределения для всех классов состояния с учетом характеристики масштаба приведены на рисунке 3.19.

Рисунок 3.19 – Восстановление законов распределения внутри классов состояния с учетом масштаба
Шаг 5. Классификацию требуется произвести на три класса, а число исходных данных при этом двадцать. Следовательно, оптимальное значение вероятности β составляет 0,79.
Шаг 6. Расчет границ классов в соответствии со значением β. На рисунке 3.20 представлено определение границ классов.

Рисунок 3.20 – Определение границ классов состояния
Шаг 7. Классификационная шкала выглядит следующим образом:
интервал 1: 
интервал 2: 
интервал 3: 
интервал 4 
интервал 5  и более
и более
В итоге участки территориальной системы классифицируются по значению характеристического признака следующим образом (рисунок 3.21):

Рисунок 3.21 – Классификация участков ТС
Приложение
Унифицированная параметрическая модель
| СV= s/M[x] | Тип закона распределения | Параметры распределения | |
| 3,333 | Гамма | α=0,09 | 𝛽=3,3333 |
| 2,5 | Гамма | α=0,16 | 𝛽=2,5 |
| Гамма | α=0,25 | 𝛽=2 | |
| 1,667 | Гамма | α=0,36 | 𝛽=1,6667 |
| 1,429 | Гамма | α=0,49 | 𝛽=1,4286 |
| 1,25 | Гамма | α=0,64 | 𝛽=1,25 |
| 1,111 | Гамма | α=0,81 | 𝛽=1,1111 |
| Экспоненциальный | α=1 | 𝛽=1 | |
| 0,91 | Вейбулла | α=1,1 | 𝛽=1,1386 |
| 0,837 | Вейбулла | α=1,2 | 𝛽=1,2703 |
| 0,776 | Вейбулла | α=1,3 | 𝛽=1,3958 |
| 0,724 | Вейбулла | α=1,4 | 𝛽=1,516 |
| 0,707 | Гамма | α=2 | 𝛽=0,7071 |
| 0,679 | Вейбулла | α=1,5 | 𝛽=1,6315 |
| 0,64 | Вейбулла | α=1,6 | 𝛽=1,743 |
| 0,605 | Вейбулла | α=1,7 | 𝛽=1,851 |
| 0,577 | Гамма | α=3 | 𝛽=0,5774 |
| 0,575 | Вейбулла | α=1,8 | 𝛽=1,9561 |
| 0,547 | Вейбулла | α=1,9 | 𝛽=2,0585 |
| 0,523 | Вейбулла | α=2 | 𝛽=2,1587 |
| 0,5 | Вейбулла | α=2,1 | 𝛽=2,2568 |
| 0,5 | Гамма | α=4 | 𝛽=0,5 |
| 0,48 | Вейбулла | α=2,2 | 𝛽=2,3532 |
| 0,461 | Вейбулла | α=2,3 | 𝛽=2,4481 |
| 0,447 | Гамма | α=5 | 𝛽=0,4472 |
| 0,444 | Вейбулла | α=2,4 | 𝛽=2,5416 |
| 0,428 | Вейбулла | α=2,5 | 𝛽=2,6339 |
| 0,413 | Вейбулла | α=2,6 | 𝛽=2,7251 |
| 0,408 | Гамма | α=6 | 𝛽=0,4082 |
| 0,399 | Вейбулла | α=2,7 | 𝛽=2,8153 |
| 0,387 | Вейбулла | α=2,8 | 𝛽=2,9047 |
| 0,378 | Гамма | α=7 | 𝛽=0,378 |
| 0,375 | Вейбулла | α=2,9 | 𝛽=2,9933 |
| 0,363 | Вейбулла | α=3 | 𝛽=3,0812 |
| 0,354 | Гамма | α=8 | 𝛽=0,3536 |
| 0,353 | Вейбулла | α=3,1 | 𝛽=3,1684 |
| 0,343 | Вейбулла | α=3,2 | 𝛽=3,2551 |
| 0,334 | Вейбулла | α=3,3 | 𝛽=3,3412 |
| 0,333 | Гамма | α=9 | 𝛽=0,3333 |
| 0,325 | Вейбулла | α=3,4 | 𝛽=3,4269 |
| 0,316 | Вейбулла | α=3,5 | 𝛽=3,5121 |
| 0,316 | Гамма | α=10 | 𝛽=0,3162 |
| 0,309 | Вейбулла | α=3,6 | 𝛽=3,5969 |
| 0,302 | Гамма | α=11 | 𝛽=0,3015 |
| 0,301 | Вейбулла | α=3,7 | 𝛽=3,6813 |
| 0,294 | Вейбулла | α=3,8 | 𝛽=3,7654 |
| 0,289 | Гамма | α=12 | 𝛽=0,2887 |
| 0,287 | Вейбулла | α=3,9 | 𝛽=3,8491 |
| 0,281 | Вейбулла | α=4 | 𝛽=3,9326 |
| 0,277 | Гамма | α=13 | 𝛽=0,2774 |
| 0,274 | Вейбулла | α=4,1 | 𝛽=4,0158 |
| 0,268 | Вейбулла | α=4,2 | 𝛽=4,0987 |
| 0,267 | Гамма | α=14 | 𝛽=0,2673 |
| 0,263 | Вейбулла | α=4,3 | 𝛽=4,1814 |
| 0,258 | Гамма | α=15 | 𝛽=0,2582 |
| 0,257 | Вейбулла | α=4,4 | 𝛽=4,2639 |
| 0,252 | Вейбулла | α=4,5 | 𝛽=4,3462 |
| 0,25 | Гамма | α=16 | 𝛽=0,25 |
| 0,247 | Вейбулла | α=4,6 | 𝛽=4,4282 |
| 0,243 | Гамма | α=17 | 𝛽=0,2425 |
| 0,242 | Вейбулла | α=4,7 | 𝛽=4,5102 |
| 0,238 | Вейбулла | α=4,8 | 𝛽=4,5919 |
| 0,236 | Гамма | α=18 | 𝛽=0,2357 |
| 0,233 | Вейбулла | α=4,9 | 𝛽=4,6735 |
| 0,229 | Гамма | α=19 | 𝛽=0,2294 |
| 0,229 | Вейбулла | α=5 | 𝛽=4,7549 |
| 0,225 | Вейбулла | α=5,1 | 𝛽=4,8362 |
| 0,224 | Гамма | α=20 | 𝛽=0,2236 |