ЛАБОРАТОРНАЯ РАБОТА 6
Цель работы: обучить студентов методам прогнозирования посредством искусственных нейронных сетей.
1 Основные сведения о нейронных сетях
Нейронные сети (НС) - исключительно мощный метод моделирования, позволяющий воспроизводить чрезвычайно сложные зависимости, так как нейронные сети нелинейны по свой природе. На протяжении многих лет линейное моделирование было основным методом моделирования в большинстве областей, поскольку для него хорошо разработаны процедуры оптимизации. Кроме того, НС справляются с "проклятием размерности", которое не позволяет моделировать линейные зависимости в случае большого числа переменных. НС учатся на примерах. Пользователь НС подбирает представительные данные, а затем запускает алгоритм обучения, который автоматически воспринимает структуру данных. При этом от пользователя, конечно, требуется какой-то набор эвристических знаний о том, как следует отбирать и подготавливать данные, выбирать нужную архитектуру сети и интерпретировать результаты.
НС индуцированы биологией, так как состоят из элементов (искусственных нейронов), функциональные возможности которых аналогичны большинству элементарных функций биологического нейрона. Эти элементы затем организуются в структуру, называемую сетью, которая может выполнять некоторые функции, свойственные в той или иной степени биологическому мозгу. На вход искусственного нейрона поступает множество сигналов, каждый из которых является выходом другого нейрона. Каждый вход умножается на соответствующий вес, аналогичный синаптической силе биологического нейрона, и все произведения суммируются, определяя уровень активации нейрона.
НС предназначены в первую очередь для решения двух проблем: классификации и регрессии. Применительно к задаче прогноза временных рядов нас интересует проблема регрессии, т.е. аппроксимации временного ряда и его экстраполяции на определенный горизонт прогноза.
В задаче прогнозирования идея использования НС сводится к тому, чтобы по имеющемуся временному ряду обучить сеть (настроить ее синаптические веса), а затем по обученной сети оценить прогнозируемые значения. В такой постановке часто применяется метод погружения, цель которого состоит в том, чтобы использовать во временном ряде два окна 
и 
фиксированных размеров n и m, соответственно, для изучения заданного набора данных. Для заданных размеров окон выдвигается предположение, что последовательность значений 
, так или иначе, связана со следующей последовательностью 
, и эти отношения, хотя и неизвестны, но определены полностью в пределах набора данных. Различные методы могут далее использоваться, чтобы найти корреляцию двух наборов значений ( и ). В случае нейронных сетей 
используется как обучающийся вектор. Рис.1 иллюстрирует общую схему метода, иногда называемого методом скользящих окон.
При прогнозировании ряда окна сдвинуты по времени с фиксированным размером шага s (s << n). Необходимо найти корреляцию вида: 
при смещении окон во временном ряду с шагом s. Выбор размера окна и размера шага критично влияют на способность любой системы предсказания идентифицировать регулярность и, таким образом, аппроксимировать скрытую связь точно. Кроме того, весьма часто требуется некоторая предварительная обработка наборов данных, чтобы получить разумную отправную точку для n, m и s.
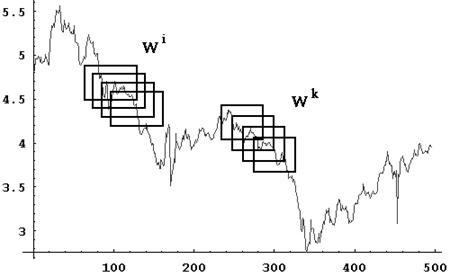
Рис.1. Схема скользящих окон
Математически задача прогноза формулируется следующим образом. Пусть для временного ряда X =(x1, x2,…,xn) требуется построить его продолжение X `=(x 1, …,xn, xn+1, xn+2). Обычно очередное значение временного ряда прогнозируется по некоторому числу его предыдущих значений (прогноз на один шаг вперед по времени). После того, как вычислено очередное предполагаемое значение, оно подставляется обратно и с его помощью (а также предыдущих значений) получается следующий прогноз - это называется проекцией временного ряда. Разобьем временной ряд на окна длиной l+ 1: x1, x2,…, xl, xl+1 , x2, x3,:, xl+1, xl+2, …, xk, xk+1,:, xl+k-1, xn и построим ИНС в виде трехслойного персептрона, имеющего l входов на входном слое, слой скрытых нейронов с подбираемым числом нейронов и выходной слой с одним нейроном.. Обучим его с помощью алгоритма обратного распространения на основе следующей обучающей последовательности: xi, xi+ 1 ,…, xl+i- 1 -> xl+i, i= 1, …,n - l.
Для используемой сети в виде трехслойного персептрона наиболее приемлемым способом обучения является метод обратного распространения ошибки. Сущность этого метода заключается в последовательном прохождении сигналов «вперед» и «назад» по всем слоям сети. При проходе «вперед» вычисляется значение выхода, которое сравнивается с его требуемой (целевой) величиной из окна Wk. На основании разницы между этими двумя значениями вычисляется ошибка, которая распространяется в направлении «назад» по сети, и методом градиентного спуска определяется величина изменения весов в каждом слое. При измененных весах на вход предъявляется новый входной вектор Wj, и процесс повторяется до тех пор, пока разница между выходным и требуемым сигналами не станет достаточно малой. Таким образом, задача обучения в этом методе сводится к предъявлению множества обучающих пар «вход - выход», за которые принимаются значения уровней ряда из окон, изменению весов после каждого прохода по сети «вперед» и «назад» до достижения приемлемой (заранее заданной) ошибки обучения.
Сеть должна иметь достаточное количество связей для запоминания последовательности. Значение хn +1 снимается с выхода построенной выше нейронной сети при подаче на вход следующего вектора (xn-l+ 1, xn-l+ 2 ,…, xn), (n - длина исходного временного ряда; l - размер окна). Значение хn +2 находится аналогично при подаче на вход сети вектора (xn-l+ 2, xn-l+ 3 ,:, xn+1). Таким образом, можно продолжать исходный ряд сколь угодно долго, находя следующие значения на основе предыдущих.
2 Работа на компьютере
Выполнение работы производится с программным пакетом Statistica; версия 6.1.
1. Открыть файл Series_G.sta с помощью команды Файл - Открыть. Этот файл находится в папке /Examples/Datasets. Данные этого файла содержат только одну переменную, которую будем использовать в качестве входной и выходной переменной одновременно.
2. Выбрать команду Нейронные сети в меню Анализ - Добыча данных для вызова Стартовой панели STATISTICA Нейронные сети. Выделить опцию Временные ряды в группе Тип задачи и указать Мастер решений на вкладке Нейронные сети Стартовая панель - Быстрый (рис.2).
Рис.2. Стартовая панель STATISTICA Нейронные сети
Нажать кнопку Переменные и выбрать переменную SERIES_G в качестве Непрерывного входа и Непрерывного выхода. Нажать кнопку OK для вызова диалога Мастер решений (рис.3).
Рис.3. Диалог Мастер решений
3. Для задач временных рядов Мастер решений требует определить число тактов временного ряда, которое будет использоваться в качестве входа нейронной сети.
Определение правильного числа входных шагов является сложной задачей. При возможности выделения явного цикла (данные в файле Series_G содержат ежемесячные записи, поэтому размер цикла равен 12 тактам), то можно указать этот цикл.
В противном случае нужно указать диапазон возможных значений, и STATISTICA Нейронные сети определит подходящий период. В этом случае рекомендуется запустить Мастер решений несколько раз с большим числом итераций.
В рассматриваемом примере зададим период, равный 12. Перейти на вкладку Временные ряды и ввести в поля Минимум и Максимум в группе Окно число 12 (рис.4).
Рис.4. Установка периода в окне Мастер решений
4. На вкладке Быстрый указать число сетей, равное 10; на вкладке Тип сети - оставить только трехслойный персептрон; на вкладке Сохранить - указать 5 сохраняемых сетей; на вкладке Сложность - число нейронов в скрытом слое принять равным от 4 до 10.
После этого нажать кнопку OK для обучения нейронной сети (рис.5).
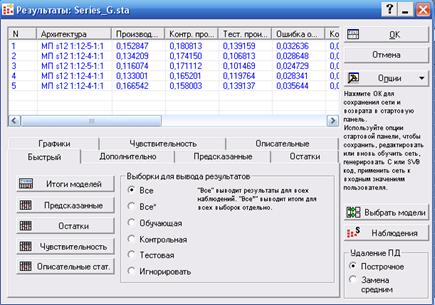
Рис.5. Окно результатов
5. Из 5 сохраненных сетей выбрать сеть с наименьшей ошибкой, нажав клавишу Выбрать модели и указав номер лучшей сети. В данном случае это сеть №3.
Рис.6. Архитектура сети (12-5-1)
6. На вкладке Дополнительно можно указать Архитектуру сети, что дает структуру НС (рис.6).
7. На этой же вкладке выделив Проекцию временного ряда и указав на вкладке Быстрый длину проекции, равной, например, 200, получим график временного ряда (рис.7). Напомним, что исходный ряд составлял 144 точки. Здесь же можно получить и значения предсказанного ряда, нажав клавишу Таблица временного ряда.
Рис.7. График временного ряда
8. На вкладке Графики можно построить зависимость наблюдаемых значений ряда от предсказанных, указав их в соответствующих окнах (рис.8).
Рис.8. Зависимость наблюдаемых значений ряда от предсказанных
Как видно из графика, точки лежат примерно на прямой линии, что свидетельствует о надежности прогноза.
Возможности пакета позволяют проводить дальнейший анализ, включая выбор других типов сети, числа нейронов в скрытом слое, количества сохраняемых сетей и т.д.
3 Задание
Сформировать временной ряд типа AR(1) длиной 100 точек и построить его прогноз на 20 точек вперед.
Вопросы к защите по работе:
1. Что имитирует нейронная сеть?
2. Каковы основные парадигмы обучения нейронных сетей?
3. Для решения каких задач предназначена в первую очередь нейронная сеть?
4. Что представляет из себя персептрон?
5. Как соотносятся окна во временном ряду с количеством нейронов в слоях персептрона?
6. Можно ли теоретически с помощью нейронной сети получить достаточно длинный горизонт прогноза?
7. В чем основная идея метода обратного распространения ошибки при обучении нейронной сети?
8. Что является подстраиваемыми элементами при обучении нейронной сети?