Теорема (Об условии возрастания/убывания монотонной функции)

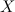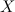Если производная функции на некотором промежутке , то функция возрастает на этом промежутке; если же на промежутке , то функция убывает на этом промежутке.

Понятие экстремума функции

Точка называется точкой локального максимума функции , если существует такая окрестность этой точки, что для всех из этой окрестности выполняется неравенство: .

Точка называется точкой локального минимума функции , если существует такая окрестность этой точки, что для всех из этой окрестности .

Значение функции в точке максимума называется локальным максимумом, значение функции в точке минимума - локальным минимумом данной функции. Локальные максимум и минимум функции называются локальными экстремумами.

Точка называется точкой строгого локального максимума функции , если для всех из окрестности этой точки будет справедливо строгое неравенство .

Точка называется точкой строгого локального минимума функции , если для всех из окрестности этой точки будет справедливо строгое неравенство .

Наибольшее или наименьшее значение функции на промежутке называется глобальным экстремумом.

Замечание

Глобальный экстремум может достигаться либо в точках локального экстремума, либо на концах отрезка.

Теорема(Необходимое условие экстремума)

Если функция имеет экстремум в точке , то ее производная либо равна нулю, либо не существует.

Точки, в которых производная равна нулю: , называются стационарными точками функции.

Точки, в которых выполняется необходимое условие экстремума для непрерывной функции, называются критическими точками этой функции. То есть критические точки - это либо стационарные точки (решения уравнения ), либо это точки, в которых производная не существует.

Замечание

Не в каждой своей критической точке функция обязательно имеет максимум или минимум.

Теорема (Первое достаточное условие экстремума)

Пусть для функции выполнены следующие условия:

1. функция непрерывна в окрестности точки ;

2. или не существует;

3. производная при переходе через точку меняет свой знак.

Тогда в точке функция имеет экстремум, причем это минимум, если при переходе через точку производная меняет свой знак с минуса на плюс; максимум, если при переходе через точку производная меняет свой знак с плюса на минус.

Если производная при переходе через точку не меняет знак, то экстремума в точке нет.

Таким образом, для того чтобы исследовать функцию на экстремум, необходимо:

1. найти производную ;

2. найти критические точки, то есть такие значения , в которых или не существует;

3. исследовать знак производной слева и справа от каждой критической точки;

4. найти значение функции в экстремальных точках.

Пример

Задание. Исследовать функцию на экстремум.

Решение. Находим производную заданной функции:

Далее ищем критические точки функции, для этого решаем уравнение :

Первая производная определена во всех точках. Таким образом, имеем одну критическую точку . Наносим эту точку на координатную прямую и исследуем знак производной слева и справа от этой точки (для этого из каждого промежутка берем произвольное значение и находим значение производной в выбранной точке, определяем знак полученной величины):

Так как при переходе через точку производная сменила свой знак с "-" на "+", то в этой точке функция достигает минимума (или минимального значения), причем .

Замечание. Также можно определить интервалы монотонности функции: так как на интервале производная , то на этом интервале функция является убывающей; на интервале производная , значит заданная функция возрастает на нем.

Ответ.