Вычисление подмножеств конечных множеств

 

Конечное множество — это множество с конечным количеством элементов, то есть число элементов — это некоторое натуральное число или 0. Ранее мы увидели, что, используя систему записи множеств, мы можем писать элементы множества в любом порядке. Например, множество {1, 2, 3} может быть при переставлении элементов местами записано шестью разными способами: {1, 2, 3}, {1, 3, 2}, {2, 1, 3}, {2, 3, 1}, {3, 1, 2}, {3, 2, 1} (каждый из элементов написан по разу).

В общем случае множество из n элементов может быть упорядочено 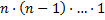способами, поскольку первый элемент можно выбрать способами, второй — и т. д. Это произведение мы обозначаем как (читается как факториал).

Например, множество из 10 элементов может быть упорядочено

способами.

Конечное множество имеет конечное число подмножеств, но сколько их? Например, рассмотрим множество {1, 2, 3}. Ниже перечислены все подмножества этого множества в соответствии с их размером :

	подмножества	число подмножеств
	⌀
	{1}, {2}, {3}
	{1,2}, {1,3}, {2,3}
	{1, 2, 3}

Таблица показывает, что множество имеет в общей сложности 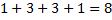подмножеств.

Упражнение 1.12

Видим, что множество из трёх элементов имеет 8 подмножеств, а множество из четырёх элементов — 16 подмножеств. Можно предположить, что множество из элементов имеет подмножеств. Чтобы это доказать, предположим следующее. С каждым подмножеством множества , состоящего из элементов, можно сопоставить строку из символов, где -й символ — это 1, если -й элемент содержится в данном подмножестве, и 0 иначе. Например, если , то строка для подмножества — это 01011. Поскольку для каждого из символов есть два варианта выбора, то всего строк, как и подмножеств, .

Теперь сосредоточимся на таком вопросе, который связан с предыдущим: сколько у множества из элементов подмножеств из элементов? Чтобы ответить на него, рассмотрим упорядоченный выбор элементов из множества. Для первого — вариантов, для второго , для последнего — . Таким образом, количество упорядоченных наборов из элементов -элементного множества равно . Но некоторые из этих наборов порождают одни и те же множества. На самом деле каждое подмножество из элементов соответствует выборам элементов. Таким образом, число различных подмножеств c элементами -элементного множества равно .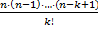

Умножив числитель и знаменатель на 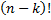, получим . Введём для этого выражения такую запись.

Например, число подмножеств из двух элементов множества из трёх элементов равно

,

что мы и получили из таблицы на странице 14.

Более интересный пример — пример лотереи, в которой участники выбирают подмножество из 6 элементов множества из 49 элементов. В этом случае возможных подмножеств, или, как их обычно называют, комбинаций,

.

Упражнение 1.13

Пример 1.5

Решение

Упражнение 1.14

Операции с множествами

Рассмотрим два множества и . Используя их, можно составить новые множества. Например:

· множество , состоящее из всех элементов, принадлежащих хотя бы одному из двух множеств;

· множество , состоящее из всех элементов, принадлежащих обоим множествам;

· множество , состоящее из всех элементов, принадлежащих первому множеству, но не принадлежащих второму, и множество , состоящее из всех элементов, принадлежащих второму, но не первому множеству.

Каждое из этих множеств — это частный случай общей конструкции множества. Рассмотрим эти конструкции по очереди.

Объединение

Множество из первого пункта списка мы называем объединением наших двух множеств. В более общем случае принимается следующее определение.

Обратите внимание, что слово «или» в этом определении используется в инклюзивном смысле «и/или», то есть состоит из элементов и элементов , включая элементы, входящие и в , и в .

Пример 1.6

Решение

Упражнение 1.15

Пока что мы дали определение объединения двух множеств. Так же можно дать и определение объединения большего числа множеств; например, объединение множеств , и 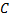— это множество .

Пересечение

Множество из второго пункта списка мы называем объединением наших двух множеств. В более общем случае принимается следующее определение.

Два множества, у которых нет общих элементов, например, и , называются непересекающимися. Тогда говорят, что ⌀.

Пример 1.7

Решение

Упражнение 1.16

Пока что мы дали определение пересечения двух множеств. Так же можно дать и определение пересечения большего числа множеств; например, пересечение множеств , и 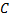— это множество .

Разность

Первое множество из третьего пункта списка мы называем вычитанием второго множества из первого, а второе — вычитанием первого множества из второго. В более общем случае принимается следующее определение.

Замечание Обратите внимание, что если , то . Также для любого ⌀.

Пример 1.8

Решение

Упражнение 1.17