Симметрия прямой призмы.

Симметрия в кубе, в параллелепипеде, в призме и пирамиде.

I. Понятие симметрии.

Симметрия встречается в природе, архитектуре, технике, быту. Симметричные творения природы - это листья, цветы, птицы, животные, творения человека - это здания, техника. В быту: мо­лотки, рубанки, лопаты, трубы. Части лица симметричны друг другу. Таким образом, симметрия бывает не только на плоскости но и в пространстве.

«Симметрия» в переводе с греческого означает «соразмерность» (повторяемость). Симметричные тела и предметы состоят из равнозначных, правильно повторяющихся в пространстве час­тей. Особенно разнообразна симметрия кристаллов. Различные кристаллы отличаются большей или меньшей симметричностью. Она является их важнейшим и специфическим свойством, отражаю­щим закономерность внутреннего строения.

Симметрия – это закономерная повторяемость элементов (или частей) фигуры или какого-либо тела, при которой фигура совмещается сама с собой при некоторых преобразованиях (вращение вокруг оси, отражение в плоскости).

Понятие симметрии включает в себя такие понятия, как: ось симметрии, центр симметрии и плоскость симметрии.

1) Ось симметрии - воображаемая ось, при повороте вокруг которой на некоторый угол, фигура совмещается сама с собой в пространстве (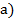

2) Плоскость симметрии делит многогранник на 2 зеркально равные части (б).

3) Центр симметрии - это точка внутри многогранника, в которой пересекаются и делятся попо­лам прямые, соединяющие одинаковые элементы многогранника (грани, рёбра, углы) (в).

Степенью симметрии называется совокупность всех элементов симметрии, которыми обладает данный многогранник.

Например, куб обладает высокой степенью симметрии, т.к. в нём присутст­вуют 3 оси симметрии четвёртого порядка, четыре оси симметрии 3 - го порядка, шесть осей второго порядка В точке пресечения осей симметрии располагается центр симмет­рии куба. Кроме того в кубе можно провести 9 плоскостей симметрии.

 

II. Симметрия в кубе.

Кубу свойственны все виды симметрии.

а) Центр симметрии (центр куба) –

точка пресечения диагоналей куба (рис 1).

Рис.1

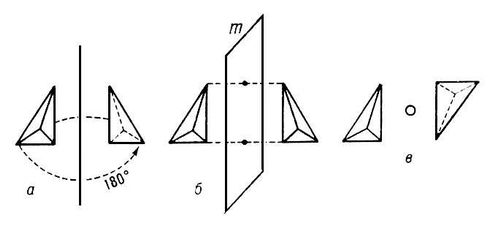
б) Плоскости симметрии (их 9):

1) 3 плоскости симметрии, проходящие через середины парал­лельных ребер (рис. 2);

2) 6 плоскостей симметрии, проходящие через противолежащие ребра (рис. 3).

 

Рис. 2

Рис. 3

в) Оси симметрии (их 13):

1)3 оси, проходящие через центры противолежащих граней (рис.4);

2) 4 оси сим­метрии, проходящие через противолежащие вершины (рис.5);

3) 6 осей, проходящие через середины про­тиволежащих рёбер (рис.6).

 

 

Рис.4 Рис.5 Рис.6

 

III. Симметрия в параллелепипеде.

а) Центр симметрии –

точка пересечения диагоналей прямоугольного

парал­лелепипеда (рис7).

Рис.7

Б) Плоскость симметрии.

3 плоскости симметрии, проходящие через середины параллельных рё­бер (рис.8).

 

 

 

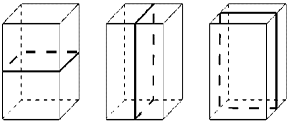
Рис.8

 

В) Оси симметрии.

3 оси симметрии, проходящие через точки пересечения диагоналей противоле­жащих граней (рис.9)

Рис.9

IV. Симметрия в призме.

Симметрия прямой призмы.

Одна плоскость симметрии, проходящая через

середины боковых рёбер (рис.10).

 

Рис.10

 

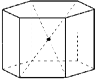2) Симметрия правильной призмы.

а) Центр симметрии.

При чётном числе сторон основания центр симметрии –

это точка пересече­ния диагоналей правильной призмы

(рис.11).

Рис.11

 

б) Плоскости симметрии:

1) плоскость, проходящая через середины

боковых рёбер (рис.12);

 

Рис.12

 

2) при чётном числе сторон основания - плоскости,

проходящие через противолежащие рёбра (рис.13).

 

Рис.13

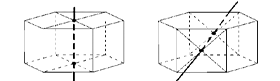
в) Ось симметрии:

а) при чётном числе сторон основания - ось симметрии проходит через центры оснований;

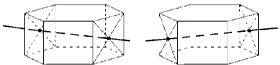б) оси симметрии, проходящие через точки пресечения диагоналей противолежащих боковых граней.

 

Рис.14