Расчетно-графическая работа

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

КОЛОМЕНСКИЙ ИНСТИТУТ (ФИЛИАЛ)

 

Государственного образовательного учреждения

Высшего профессионального образования

 

«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ОТКРЫТЫЙ УНИВЕРСИТЕТ»

_______________________________________________________________________

 

КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ и ФИЗИКИ

Н.Н. Адамушко

МАТЕРИАЛЫ

Расчетно-графической работы

По математике

Дифференцирование и интегрирование функции многих переменных

Для студентов 2-го курса (1 семестр) специальностей

151900. 62 -КТО, 141100. 62 -ЭМС, 270800. 62 -С

Очная форма обучения

Коломна

КИ (ф) МГОУ - 2012

 

 

УДК 517.5/.8

ББК 22.161.5

А28

Рецензент:

кандидат физ.-мат. наук, доцент кафедры высшей математики и физики КИ(ф)МГОУ

Балабан Е.И.

 

Адамушко Н.Н.

Материалырасчетно-графической работы по математике Дифференцирование и интегрирование функции многих переменных для студентов 2го курса (1 семестр) специальностей 151900.62-КТО, 141100.62-ЭМС, 270800.62-С – Коломна: КИ (ф) МГОУ, 2012, 40 с.

 

Учебно-методическое пособие содержит задания (30 вариантов) и требования к выполнению РГР математике по курсу «Дифференцирование и интегрирование функции многих переменных ». Предназначено для студентов 2го курса (1 семестр) специальностей 151900.62-КТО, 141100.62-ЭМС, 270800.62-С

 

Рассмотрено на заседании

кафедры высшей математики и физики

24.10.2012г., протокол №2

 

Содержание

1. Требования к выполнению расчетно-графических работ...........................4

2. Правила выполнения расчетно-графических работ………………………..4

3. Требования к оформлению расчетно-графической работы.……………...4

4. Срок представления расчетно-графической работы …...……………...…..4

5. Образец оформления титульного листа…………………………………….5

6. Содержание расчетно-графической работы ………………………………..6

Требования к выполнению расчетно-графической работы

1. Каждый студент 2-го курса в 1-м семестре должен выполнить одну расчетно-графическую работу по математике.

2. Задания выбираются по номерам списка учебной группы.

3. Требования к оформлению работы и титульного листа приведены далее.

4. Выполненные РГР должны быть представлены до указанного срока.

 

Правила выполнения расчетно-графической работы

1. При выполнении контрольной расчетно-графической работы необходимо строго придерживаться указанных ниже правил. Работа, выполненная без соблюдения этих правил не зачитывается и возвращается для переработки.

2. Контрольная работа должна быть выполнена в отдельной тетради в клетку синими или черными чернилами.

3. В заголовке работы на обложке тетради должны быть ясно написаны фамилия студента, номер зачетной книжки, номер контрольной работы, название дисциплины. В конце работы следует поставить дату ее выполнения и расписаться.

4. В работу должны быть включены все задачи, указанные в задании, строго по положенному варианту.

5. Решения задач следует располагать в порядке номеров, указанных в задании, сохраняя номера задач.

6. Перед решением каждой задачи надо полностью написать ее условие. В том случае, если несколько задач, из которых студент выбирает задачу своего варианта, имеют общую формулировку, следует, переписывая условия задачи, заменить общие данные конкретными, взятыми из соответствующего номера.

7. Решения задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая четкие и соразмерные необходимые чертежи.

 

Требования к оформлению работы

Формат: А4. WORD 2003: кейгль 14, «times new roman», поля: левое-30 мм, правое-10 мм, верх и низ-20 мм. Межстрочный интервал: полуторный. Формулы: Equation или Math Type Графика: любой редактор, импортируемый в WORD.

Объём: без ограничений.

 

Срок представления РГР

РГР должна быть сдана до 16 декабря 2012г. (15 декабря последний день)

 

 

Образец оформления титульного листа

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

КОЛОМЕНСКИЙ ИНСТИТУТ (ФИЛИАЛ)

 

Государственного образовательного учреждения

Высшего профессионального образования

 

«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ОТКРЫТЫЙ УНИВЕРСИТЕТ»

_______________________________________________________________________

 

КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ и ФИЗИКИ

РГР

Название темы

 

 

Автор: студент группы

№ группы

Фамилия И.О.

№ зачетной книжки

Рецензент: доцент(профессор)

Фамилия И.О.

Дата представления

 

Коломна-2012

 

Расчетно-графическая работа

«Дифференцирование и интегрирование функции многих переменных»

В состав расчетно-графической работы входят семь заданий по темам, изучаемым в первом семестре второго курса: дифференцирование сложной функции, нахождение производной по направлению, определение угла между градиентами, вычисление экстремальных значений функции двух переменных, изменение порядка интегрирования в двойном интеграле, вычисление криволинейного интеграла, решение задач по теории поля.

 

ВАРИАНТ №1

1 Продифференцировать сложные функции:

а) найти ; , , .

б) найти частные производные функции

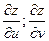
, если ;

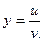
2 Найти производную скалярного поля в точке по направлению нормали к поверхности , проходящей через эту точку образующей острый угол с положительным направлением оси .

3 Найти угол между градиентами скалярных полей , в точке .

4 Найти наименьшее и наибольшее значения функции двух переменных в замкнутой области Д с заданными границами Г

5 Изменить порядок интегрирования в двойном интеграле.

Сделать чертеж области интегрирования.

6 Вычислить криволинейный интеграл 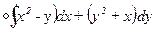по замкнутому контуру С = ОАВО, где О – начало координат; ОА – отрезок оси ОХ; ВО – отрезок оси ОУ; линия АВ дана уравнением x + y-1 = 0. Вычисление провести двумя способами: непосредственно и по формуле Грина.

7 Найти циркуляцию векторного поля по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OX. Вычисления провести двумя способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру; б) по теореме Стокса.

 

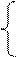
Г: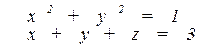

ВАРИАНТ №2

1 Продифференцировать сложные функции:

а) найти ; , , .

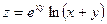б) найти частные производные функции

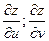
, если ;

2 Найти производную скалярного поля в точке по направлению нормали к поверхности 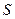, проходящей через эту точку образующей острый угол с положительным направлением оси .

3 Найти угол между градиентами скалярных полей , в точке .

4 Найти наименьшее и наибольшее значение функции в замкнутом треугольнике, ограниченном осями координат и прямой

5 Изменить порядок интегрирования в двойном интеграле

Сделать чертеж области интегрирования.

 

6 Проверить, является ли заданное выражение дифференциалом некоторой функции U (x,y) и в случае положительного ответа найти U с помощью криволинейного интеграла

(sin²y-ysin2x) dx + (xsin2y+cos²x+1) dy

7 Найти циркуляцию векторного поля по контуру . Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести двумя способами: а) непосредственно, вычисляя интеграл векторного поля по контуру £; б) по теореме Стокса

:

 

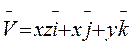
ВАРИАНТ №3

1 Продифференцировать сложные функции

а) найти ; , , .

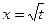б) найти частные производные функции

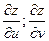
, если ;

2 Найти производную скалярного поля в точке по направлению нормали к поверхности 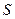, проходящей через эту точку образующей острый угол с положительным направлением оси .

3 Найти угол между градиентами скалярных полей , в точке .

4 Найти наименьшее и наибольшее значение функции в треугольнике со сторонами

5 Изменить порядок интегрирования в двойном интеграле

Сделать чертеж области интегрировании

6 Вычислить криволинейный интеграл по замкнутому контуру С = ОАВО; где О-начало координат;ОА-отрезок оси ОХ; ВО- отрезок оси ОУ; линия АВ дана уравнением Вычисление провести двумя способами: непосредственно и по формуле Грина

7 Вычислить поток поля вектора через треугольник, вырезанный из плоскости x+y+2z-2=0 координатными плоскостями, в том направлении к плоскости, которое образует с осью ОУ острый угол

ВАРИАНТ №4

1 Продифференцировать сложные функции

а) найти ; , , .

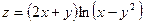б) найти частные производные функции

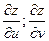
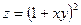, если ;

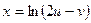2 Найти производную скалярного поля в точке по направлению нормали к поверхности 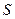, проходящей через эту точку образующей острый угол с положительным направлением оси .

3 Найти угол между градиентами скалярных полей , в точке .

4 Найти наименьшее и наибольшее значение функции двух переменных в замкнутой области Д с заданными границами Г

;

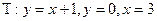
5 Изменить порядок интегрирования в двойном интеграле

6 Проверить, является ли заданное выражение дифференциалом некоторой функции U (x,y) и в случае положительного ответа найти U (x,y) с помощью криволинейного интеграла.

7 Найти циркуляцию векторного поля по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести двумя способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса

a. F:

 

 

ВАРИАНТ №5

 

1 Продифференцировать сложные функции

а) Найти ; , , .

б) Найти частные производные функции

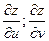
, если ;

2 Найти производную скалярного поля в точке по направлению нормали к поверхности 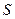, проходящей через эту точку образующей острый угол с положительным направлением оси .

3 Найти угол между градиентами скалярных полей , в точке .

4 Изменить порядок интегрирования в двойном интеграле

Сделать чертеж области интегрирования.

5 Найти наименьшее и наибольшее значение функции двух переменных в замкнутой области Д с заданными границами Г

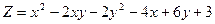
6 Поверить, является ли заданное выражение дифференциалом некоторой функции (x,y) и в случае положительного ответа найти И(x,y) с помощью криволинейного интеграла.

7 Найти циркуляцию векторного поля по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисление провести двумя способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса

Г: (1-ый октант)

 

ВАРИАНТ №6

1 Продифференцировать сложные функции

а) найти ; , , .

б) найти частные производные функции

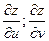
, если ;

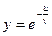
2 Найти производную скалярного поля в точке по направлению нормали к поверхности 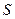, проходящей через эту точку образующей острый угол с положительным направлением оси .

3 Найти угол между градиентами скалярных полей , в точке .

4 Найти наименьшее и наибольшее значение функции двух переменных в замкнутой области Д с заданными границами Г

,

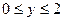
5 Изменить порядок интегрирования в двойном интеграле

Сделать чертеж области интегрирования

6 Проверить, является ли заданное выражение дифференциалом некоторой функции U (x,y) и в случае положительного ответа найти U (x,y) с помощью криволинейного интеграла.

7 Найти циркуляцию векторного поля по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести двумя способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.

Г:

ВАРИАНТ №7

 

1. Продифференцировать сложные функции

а) найти ; , , .

б) найти частные производные функции

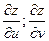
, если ;

2 Найти производную скалярного поля в точке по направлению нормали к поверхности 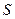, проходящей через эту точку образующей острый угол с положительным направлением оси .

3 Найти угол между градиентами скалярных полей , в точке .

4 Изменить порядок интегрирования в двойном интеграле

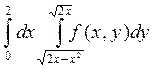
Сделать чертеж области интегрирования

 

5 Найти наименьшее и наибольшее значение функции двух переменных в замкнутой области Д с заданными границами Г

6 Проверить, является ли заданное выражение дифференциалом некоторой функции U(x,y) и в случае положительного ответа найти U (x,y) с помощью криволинейного интеграла.

7 Найти циркуляцию векторного поля по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести двумя способами: а)непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б)по формуле Стокса.

Г:

ВАРИАНТ №8

1. Продифференцировать сложные функции

а) найти ; , , .

б) найти частные производные функции

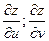
, если ;

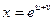2 Найти производную скалярного поля в точке по направлению нормали к поверхности 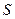, проходящей через эту точку образующей острый угол с положительным направлением оси .

3 Найти угол между градиентами скалярных полей , в точке .

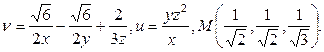
4 Изменить порядок интегрирования в двойном интеграле

Сделать чертеж области интегрирования.

 

5 Найти наименьшее и наибольшее значение функции двух переменных в замкнутой области Д с заданными границами Г

6 Найти циркуляцию векторного поля по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ.Вычисления провести двумя способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по формуле Стокса

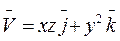Г:

7 Проверить, является ли заданное выражение дифференциалом некоторой функции U (x,y) и в случае положительного ответа найти U (x,y) с помощью криволинейного интеграла.

ВАРИАНТ №9

1. Продифференцировать сложные функции

а) найти ; , , .

б) найти частные производные функции

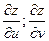
, если ;

2 Найти производную скалярного поля в точке по направлению нормали к поверхности 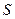, проходящей через эту точку образующей острый угол с положительным направлением оси .

3 Найти угол между градиентами скалярных полей , в точке .

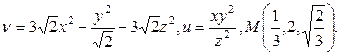
4 Изменить порядок интегрирования в двойном интеграле

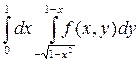
Сделать чертеж области интегрирования.

5 Найти наименьшее и наибольшее значение функции двух переменных в замкнутой области Д с заданными границами Г

6 Проверить, является ли заданное выражение дифференциалом некоторой функции U (x,y) и в случае положительного ответа найти U (x,y) с помощью криволинейного интеграла.

7 Найти циркуляцию векторного поля по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести двумя способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.

Г:

 

ВАРИАНТ №10

1 Продифференцировать сложные функции

а) найти ; , , .

б) найти частные производные функции

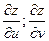
, если ;

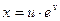2 Найти производную скалярного поля в точке по направлению нормали к поверхности 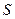, проходящей через эту точку образующей острый угол с положительным направлением оси .

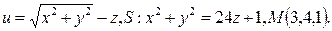
3 Найти угол между градиентами скалярных полей , в точке .

4 Найти уравнение касательной плоскости и уравнение нормали к поверхности

в точке А(2,1,2)

5 Поле образовано силой F{y;a }, определить работу при перемещении массы по контуру, образованному полуосями координат и первой четвертью эллипса x = a cost, y = bsint

6 Дан вектор и плоскость Р. Плоскость [Р] вместе с координатными плоскостями образует поверхность некоторой пирамиды. Требуется: С помощью формулы Остроградского найти поток поля вектора через поверхность пирамиды в направлении внешней нормали.

7 Найти циркуляцию поля вектора вдоль линии пересечения плоскости [Р] с координатными плоскостями непосредственно и по формуле Стокса, применяя в формуле Стокса за поверхность, по которой производится интегрирование, три грани пирамиды, лежащие в координатных плоскостях. При этом то направление обхода линии интегрирования следует считать положительным, при котором точка пробегает ее по ходу часовой стрелки, если смотреть от начала координат.

 

ВАРИАНТ №11

1 Продифференцировать сложные функции

а) найти ; , , .

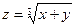б) найти частные производные функции

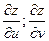
, если ;

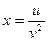2 Найти производную скалярного поля в точке по направлению нормали к поверхности 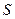, проходящей через эту точку образующей острый угол с положительным направлением оси .

3. Найти угол между градиентами скалярных полей , в точке .

4 Найти векторные линии в векторном поле .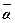

.

5 Изменить порядок интегрирования в двойном интеграле:

Сделать чертеж области интегрирования.

6 Вычислить криволинейный интеграл по замкнутому контуру С=ОАВО, где О-начало координат, ОА-отрезок оси ОХ, ВО-отрезок осиОУ, линия АВ дана своим уравнением x² + y²-1 = 0. Вычисление провести 2 способами: непосредственно и по формуле Грина.

7 Найти циркуляцию векторного поля по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести 2 способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.

a. Г:

 

ВАРИАНТ №12

1 Продифференцировать сложные функции

а) найти ; , , .

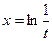б) найти частные производные функции

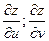
, если ;

2 Найти производную скалярного поля в точке по направлению нормали к поверхности 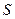, проходящей через эту точку образующей острый угол с положительным направлением оси .

3 Найти угол между градиентами скалярных полей , в точке .

 

4 Найти наименьшее и наибольшее значения функции двух переменных

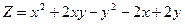В замкнутой области Д с заданными границами

Г:

5 Изменить порядок интегрирования в двойном интеграле:

Сделать чертеж области интегрирования.

6 Вычислить криволинейный интеграл по замкнутому контуру С = ОАВО, где О - начало координат, ОА- отрезок оси ОХ, ВО-отрезок оси ОУ, линия АВ дана своим управлением x²+y²-4 = 0. Вычисление провести 2 способами непосредственно и по формуле Грина.

7 Найти циркуляцию векторного поля по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести двумя способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.

Г:

 

ВАРИАНТ №13

1 Продифференцировать сложные функции

а) найти ; , , .

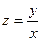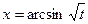б) найти частные производные функции

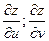
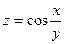, если ;

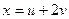2 Найти производную скалярного поля в точке по направлению нормали к поверхности 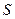, проходящей через эту точку образующей острый угол с положительным направлением оси .

3 Найти угол между градиентами скалярных полей , в точке .

4 Найти наименьшее и наибольшее значения функции двух переменных

. В замкнутой области Д с заданными границами Г:

5 Изменить порядок интегрирования в двойном интеграле:

Сделать чертеж области интегрирования

6 Вычислить криволинейный интеграл по замкнутому контуру С=ОАВО, где О –начало координат, ОА – отрезок оси ОХ, ВО – отрезок оси ОУ, линия АВ дана своим уравнением x² + 4y² – 1 = 0 Вычисление провести двумя способами: непосредственно и по формуле Грина.

7 Найти циркуляцию векторного поля по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисление провести 2 способами: а) непосредственно, вычисляя линейный интеграл векто