Пространство и время
Невозможно отчетливо осмыслить ни один из законов механики – науки о движении тел – без того, чтобы так или иначе не определить понятий пространства и времени. Эту необходимость определённых представлений о пространстве и времени глубоко понимал основоположник законов механики великий Ньютон. Все представления о природе, и в том числе представления о пространстве и времени, возникают из опыта, в частности из повседневного житейского опыта. Чем более раннюю стадию науки мы рассматриваем, чем меньше опытных фактов имеется в распоряжении науки, тем беднее и наивнее представления о пространстве. В науке XVII века были еще достаточно сильны субъективные наивные представления об абсолютности движения, полученные из ограниченного опыта движения тел по Земле. Ньютон полагал, что существуют пространство и время, никак не связанные ни с происходящими в них явлениями, ни между собой. Пространство и время служат как бы сценой для всех явлений природы, содержание которых нисколько не влияет на неё: сцена всегда остаётся одной и той же. Такое пространство и время получили название абсолютного пространства и времени – они одинаковы и неизменны во всех случаях, при всех явлениях.
Сам Ньютон следующим образом определял абсолютные пространство и время: “Абсолютное пространство в силу своей природы и безотносительности к какому-либо другому объекту всегда остается одинаковым и неподвижным”.
“Абсолютное, истинное и математическое время само по себе и в силу своей природы протекает равномерно и безотносительно к какому-нибудь другому объекту. Оно называется также длительностью”.
Но наряду с абсолютным пространством Ньютон допускал также относительное пространство и время, которые он определял следующим образом:
“Относительное пространство является мерилом, или подвижной частью, первого (абсолютного), которую мы воспринимаем чувственно, благодаря ее положениям относительно других тел, и обычно считаем неподвижным”. “Таким образом в обыденных человеческих отношениях мы пользуемся и довольно целесообразно вместо абсолютных положений и движений относительными; в естествознании, напротив, следует отвлечься от чувственных данных. В самом деле, вполне возможно, что в природе нет действительно покоящегося тела, к которому можно относить все положения и движения”.
“Относительное, кажущееся и обыкновенное время есть чувственная и внешняя, иногда очень точная, иногда непостоянная мера длительности, которой обычно пользуются вместо истинного, как, например, час, сутки, месяц, год”. “Естественные сутки, которые как мерило времени считаются все одинаковыми, в действительности не одинаковы. Астрономы исправляют это неравенство, измеряя движение небесных тел истинным временем. Возможно, что не существует вовсе равномерного движения, при помощи которого можно было бы точно измерять время, все движения могут ускоряться или замедляться, но течение абсолютного времени не может изменяться. Одна и та же длительность и одна и та же инерция существуют для всех вещей”.
Высказанные в этих цитатах представления о пространстве и времени лежат в основе классической механики, их придерживались вплоть до появления исследований конца XIX века. Из высказываний Ньютона видно, что он отделял абсолютное пространство и абсолютное истинное и математическое время от пространства и времени, с которыми мы имеем дело на практике: измеряя пространство, мы измеряем расстояние одного тела от другого, а измеряя время, мы отмечаем различные положения стрелки на каких-то определенных материальных часах. Ньютон, вероятно, ощущал затруднения, связанные с попытками уловить бег истинного, математического времени и измерить абсолютное пространство. Тем не менее он предполагал, что такое абсолютное пространство и время все же существуют и остались бы существовать, если бы даже все тела, которые можно принять за системы отсчета, были уничтожены. Абсолютное пространство и время рассматривались Ньютоном как нечто, совершенно не связанное с движущейся материей, подобно сосуду, который можно наполнить жидкостью, а можно и оставить пустым.
Какие же выводы о движении тел позволяют сделать представления Ньютона о пространстве и времени? Если существует абсолютное пространство, то для определения пложения тела не нужна материальная система отсчета. Можно определить положение тела в абсолютном пространстве в каждый момент времени (речь идет об абсолютном времени) и, следовательно, найти движение тела в абсолютном пространстве. Это и будет абсолютное движение тела, то есть то “истинное” движение, о котором говорилось ранее. Таким образом, с точки зрения Ньютона, следует отличать непосредственно наблюдаемые относительные движения тел от истинного абсолютного движения в абсолютном пространстве.
Математическая формулировка свойств пространства и времени выражается в виде системы геометрических понятий и связей между ними. В качестве “строительного материала” геометрия использует идеализированные образы свойств материальных объектов реального мира, такие, как точка, линия, поверхность, объем. С помощью этих образов создается геометрическая модель реального мира. Формирование геометрии как науки было завершено примерно две с половиной тысячи лет тому назад Евклидом. Долго казалось, что вопрос о соотношении геометрии с реальным миром даже не возникает, потому что единственной мыслимой моделью реального мира была геометрия Евклида. В дальнейшем было показано, что в принципе существует бесчисленное множество других внутренне непротиворечивых моделей – неевклидовых геометрий. Поэтому вопрос о том, какая модель, или геометрия, правильно отражает свойства реального мира, может быть решен только экспериментально путем сравнения всех выводов из этой модели с той ситуацией, какая существует в реальном мире.
В настоящее время изучены многие физические явления, которые позволяют сделать вывод о границах применимости геометрии Евклида. Результат можно сформулировать так: Евклидова геометрия достаточно точно описывает геометрические соотношения реального мира начиная с расстояний, раз в десять меньших, чем размеры ядер, то есть с расстояний 10–16м, до расстояний, близких к “размерам Вселенной”, то есть расстояний 1026м 
1010световых лет. Однако на этих расстояниях (порядка 10 млрд. световых лет) должна начать проявляться неевклидовость пространства, если справедливы предсказания теории относительности. Есть все основания думать, что на расстояниях, меньших 10–16м, геометрия Евклида продолжает быть справедливой, но неизвестно, до сколь малых расстояний.
Однако утверждение о справедливости геометрии Евклида вблизи поверхности Земли правильно лишь с добавлением оговорки “с очень большой точностью”. В абсолютном же смысле это утверждение несправедливо. Общая теория относительности утверждает, что при наличии поля тяготения геометрия не является Евклидовой.
Таким образом, в классической механике пространство считается Евклидовым, а время единым.
Системы отсчета
Как уже отмечалось, в механике под движением понимается изменение положения тела в пространстве с течением времени. Причем под положением тела понимается относительное положение, то есть положение относительно других тел. Отсюда следует, что если мы собираемся изучать движения какого-либо тела, то необходимо указать, по отношению к каким другим телам происходит данное движение.
Движение происходит как в пространстве, так и во времени. Поэтому для описания движения необходимо определять время, что делается с помощью часов. Совокупность неподвижных друг относительно друга тел, по отношению к которым рассматривается движение, и часов, отсчитывающих время, образуют пространственно-временную систему отсчета.
Системы отсчета необходимы для описания движения. Поэтому в системах отсчета, как в физических телах, абстрагируются от всего, что связано с их конкретным строением и внутренними свойствами. Важно только то, как выглядит по отношению к ним пространство и как течет время.
Описать движение тела означает указать для каждого момента времени положение тела в пространстве. Для того, чтобы задать состояние механической системы, нужно указать положение всех тел, образующих систему, как функцию времени. Типичная задача механики заключается в том, чтобы, зная состояние системы в некоторый начальный момент времени и законы, управляющие движением, определить состояния системы во все последующие моменты времени.
Описанием движения тел, безотносительно к причинам его вызвавшим, занимается кинематика. В различных системах отсчета движение одного и того же тела выглядит по-разному. В кинематике при выборе системы отсчета руководствуются лишь соображениями целесообразности, определяющимися конкретными условиями. Так, при рассмотрении движения тел на Земле, удобно связать систему отсчета с Землей, при рассмотрении движения самой Земли систему отсчета удобно связать с Солнцем. Никаких принципиальных преимуществ одной системы отсчета по сравнению с другой в кинематике указать нельзя. Все системы отсчета кинематически эквивалентны. Только в динамике, изучающей движение в связи с причинами, вызвавшими движение, выявляется принципиальное преимущество определенного класса систем отсчета, так называемых инерциальных систем отсчета.
Материальная точка
Простейшим объектом, движение которого изучает классическая механика, является материальная точка.
Материальной точкой называется макроскопическое тело, размеры которого в рассматриваемом движении можно не принимать во внимание и считать, что все вещество тела сосредоточено в одной геометрической точке.
Разумеется, в природе материальных точек нет. Это абстракция, идеализированный образ реально существующих тел. Можно ли принять данное тело за материальную точку, зависит не столько от самого тела, сколько от характера движения этого тела, а также от содержания вопросов, на которые нужно получить ответ. Абсолютные размеры тела при этом не имеют значения. Важны относительные размеры, то есть отношение размеров тел к некоторым расстояниям, характерным для рассматриваемого движения. Например, Землю при рассмотрении ее орбитального движения вокруг Солнца можно с большой точностью принять за материальную точку (радиус орбиты Земли R С = 1,5×1011м; радиус Земли R З= 6,4×106м). Такая идеализация сильно упрощает задачу об орбитальном движении Земли, сохраняя, однако, все существенные черты этого движения. Но эта идеализация не годится при рассмотрении вращения Земли вокруг собственной оси, поскольку бессмысленно говорить о вращении материальной точки вокруг собственной оси.
Механика одной материальной точки в классической механике является основой для изучения механики вообще. С классической точки зрения произвольное макроскопическое тело или систему тел можно мысленно разбить на малые макроскопические части, взаимодействующие между собой. Каждую из этих частей можно принять за материальную точку. Тем самым изучение движения произвольной системы тел сводится к изучению движения системы взаимодействующих материальных точек. Естественно поэтому начать изучение классической механики с механики одной материальной точки, а затем перейти к изучению системы материальных точек.
1. 4. Способы описания движения материальной точки.
Скорость. Ускорение
Существует три способа описания движения точки: векторный, координатный и естественный. Рассмотрим их последовательно.
Векторный способ
Рис. 1.1
|
В этом способе положение движущейся точки А задают вектором 
, проведенным из некоторой неподвижной точки О выбранной системы отсчета в точку А. Этот вектор называется радиус-вектором. При движении точки А ее радиус-вектор меняется в общем случае как по модулю, так и по направлению, то есть радиус-вектор является функцией времени 
. Геометрическое место концов радиус-вектора называют траекторией точки А.
Поместим начало системы отсчета в точку О. Обозначим радиус-вектор начального положения точки А через 
, а радиус-вектор конечного положения через 
. Если за промежуток времени 
точка А переместилась из положения 1 в положение 2, то вектор 
называется вектором перемещения точки. Длина участка траектории между точками 1 и 2 называется путем или расстоянием, пройденным точкой.
Отношение 
называется средней скоростью материальной точки за время :
.
Вектор средней скорости совпадает по направлению с вектором перемещения.
Помимо средней скорости можно ввести понятие мгновенной скорости, то есть скорости в каждый момент времени. Мгновенная скорость определится следующим образом:
.
При уменьшении промежутка времени вектор перемещения будет поворачиваться вокруг точки 1 и в пределе займет положение касательной к траектории в точке 1. Таким образом, мгновенная скорость равна производной от радиус-вектора по времени и направлена по касательной к траектории в данной точке в сторону движения. Мгновенная скорость характеризует быстроту 
изменения радиус-вектора со временем. Модуль мгновенной скорости 
. Следует иметь ввиду, что в общем случае 
.
Движение материальной точки характеризуется также ускорением. Вектор ускорения 
определяет быстроту изменения вектора скорости, следовательно, ускорение – это производная скорости по времени
,
Направление вектора ускорения совпадает с направлением вектора приращения скорости 
. Модуль вектора ускорения равен
.
Таким образом, зная зависимость радиус-вектора от времени, можно найти скорость и ускорение точки в каждый момент времени.
Можно поставить и обратную задачу: найти радиус-вектор и скорость материальной точки, если известна зависимость ускорения от времени. Для решения этой задачи недостаточно знать только зависимость ускорения от времени, необходимо еще знать так называемые начальные условия, а именно скорость 
и радиус-вектор 
в некоторый начальный момент времени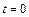 
. Рассмотрим простейший случай, когда в процессе движения ускорение остается постоянным. За промежуток времени 
элементарное приращение скорости
.
Проинтегрируем последнее выражение, тогда получим
,
где 
– постоянная интегрирования. Ее можно найти из начальных условий: если при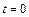 
, то 
. Следовательно,
.
Чтобы найти зависимость от времени радиус-вектора, проинтегрируем уравнение
.
После интегрирования получим
,
где 
– постоянная интегрирования. Так как при ,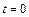 
, то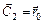 
, и, следовательно,
.
Координатный способ
Рис. 1.2
|
В этом способе с выбранным телом отсчета жестко связывают определенную систему координат. Выбор той или иной системы координат определяется рядом соображений: характером или симметрией задачи, постановкой вопроса, а также стремлением упростить само решение. На практике наиболее часто используются следующие системы координат: прямоугольная декартова, цилиндрическая и сферическая. На рис. 1.2 представлена прямоугольная декартова система координат. Различают правую и левую систему координат, которые не могут быть совмещены друг с другом никакими перемещениями и вращениями в пространстве. Они отличаются направлением осей координат 
. Система координат является правой, если при взгляде на плоскость 
в положительном направлении оси 
совмещение оси 
с осью 
по кратчайшему пути происходит в результате вращения по часовой стрелке, если против – система считается левой. В физике чаще всего применяется правая система. Во всяком случае необходимо знать, какая система координат используется, так как при переходе от правой к левой системе координат в некоторых формулах изменяются знаки.
Положение любой точки в декартовой системе координат может быть охарактеризовано координатами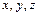 
При этом радиус-вектор точки тоже может быть выражен через ее координаты:
,
где 
, 
, 
– координатные орты, то есть единичные векторы, направленные вдоль координатных осей, 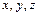– проекции радиус-вектора на оси системы координат.
Вектор мгновенной скорости можно найти, продифференцировав радиус-вектор по времени:
.
С другой стороны, вектор скорости можно разложить по осям декартовой системы координат
.
Из сопоставления двух последних выражений получим, что проекции вектора скорости на оси декартовой системы координат определятся следующим образом:
, 
, 
.
Продифференцировав вектор скорости по времени, можно найти вектор ускорения
.
Как и вектор скорости можно разложить по осям декартовой системы координат
.
Тогда проекции вектора ускорения на оси декартовой системы координат определятся следующим образом:
, 
, 
.
Модули векторов скорости и ускорения можно определить через их проекции на оси декартовой системы координат:
, 
.
Направления этих векторов можно задать через направляющие косинусы:
, 
, 
,
где 
– углы между вектором скорости и направлениями координатных осей .
Таким образом, зная 
, 
, 
, можно определить вектора скорости и ускорения. Кроме того, можно решить и ряд других вопросов: найти траекторию точки, зависимость пройденного ею пути от времени; зависимость скорости от положения точки и другие.
Рис. 1.3
|
В цилиндрической системе координат положение любой точки также характеризуется тремя числами. Этими числами являются координата Z, расстояние 
от проекции точки на плоскость XY до начала координат и угол 
между осью X и прямой r (рис. 1.3). Эти координаты связаны с декартовыми следующими формулами преобразования:
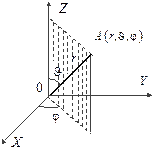Рис. 1.4
|
В сферической системе координат (рис.1.4). положение точки определяется расстоянием r до начала координат и углами 
и . Преобразование от сферических к декартовым координатам производится по формулам
Решение обратной задачи проводится, как и в векторном способе описания движения, путем интегрирования.