При анализе динамических стационарных линейных уравнений, например, вида:
(1)
с уравнением выходов:
(2)
обычно используется справедливый для них принцип суперпозиции, так как искомое решение состоит из общего решения уравнения “свободного” или “собственного” движения:
, (3)
и частного решения уравнения “вынужденного” движения:
. (4)
Математическую модель (1), (2), которая может быть представлена в виде:
(5)
принято называть моделью вход-состояние-выход [2]. Ей соответствует скалярное дифференциальное уравнение S-го порядка:
,(6)
которое обычно называют моделью вход-выход.
В моделях (5) и (6) приняты следующие обозначения: 
– выходная переменная, 
– входной сигнал, 
– порядок производной выходной переменной, в явном виде зависящей от переменных 
, 
и 
– постоянные коэффициенты.
Как известно, решением дифференциального уравнения (6) или, соответственно, системы (5), является функция времени 
или, соответственно, вектор-функция 
, обращающие данное уравнение (систему) в тождество и удовлетворяющая заданным начальным условиям следующего вида:
(7)
для уравнения (6), т.е. начальным значением переменной 
и ее производными до (S -1) - го порядка включительно. Для модели вида (5) начальными условиями являются координаты вектора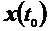 
, т.е.:
. (8)
 |
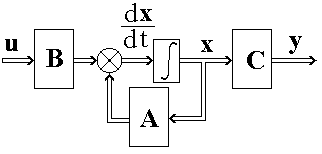Структурная схема, отображающая уравнения (1) и (2), приведена на Рис.1.
Рис.1. Структурная схема векторно-матричного стационарного линейного уравнения состояний и выходов (1) и (2).
Рассмотрим случай, когда эта задача может быть представлена структурной схемой Рис.2.
Рис.2. Структурная схема системы: 
– передаточная функция системы (в замкнутом состоянии), 
– изображение по Лапласу сигнала на входе системы (управление или возмущение) 
– изображение по Лапласу сигнала на выходе системы.
Пусть на вход системы Рис.2 подается нормированный случайный сигнал вида “белый шум”, интенсивность которого определяется дисперсией 
, а спектральная плотность 
, связанная с автокорреляционной функцией 
выражением:
(9)
Если известна импульсная передаточная функция системы Рис.2 в виде 
, такой, что
, (10)
где 
– амплитудно-частотная характеристика (АФХ) системы Рис.2 при замене в передаточной функции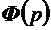 
оператора 
на 
, то на выходе такой системы будет иметь место случайный стационарный сигнал с автокорреляционной функцией вида:
. (11)
Поскольку
, (12)
то
. (13)
Так как
, (14)
то (13) перепишется в виде:
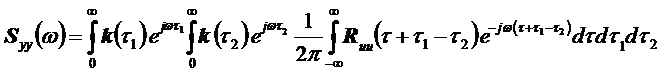.(15)
По аналогии с (12)
. (16)
Подстановка правой части (16) в (15) с заменой на левую часть (16) приводит к следующему результату:
(17)
Поэтому, спектральная плотность на выходе системы определится следующим образом:
, (18)
так как с учетом (10):
, (19)
(20)
где 
– вещественная и 
– мнимая частотные характеристики этой системы, причем:
. (21)
Таким образом, спектральная плотность сигнала на выходе системы Рис.2 равна:
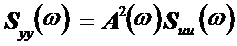. (22)
Корреляционная функция этого сигнала равна:
. (23)
а дисперсия:
. (24)
В заключение отметим, что спектральная плотность под интегралом в (24) является симметричной функцией относительно 
. Поэтому справедливо утверждение, что
. (25)
Если на вход системы Рис.2 подается случайный сигнал типа “белого шума”, т.е.:
, (26)
тогда:
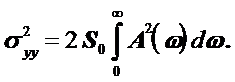(27)
Но при 
, где 
– коэффициент усиления системы
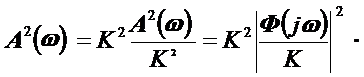(28)
Подставив (28) в (27), получим:
(29)
где
. (30)
В (30) 
– эффективная полоса пропускания частот системы Рис.2. Если в ее пределах спектральная плотность на входе системы постоянна, то такой сигнал можно считать “белым шумом” по отношению к этой системе.
Вероятностная оценка показателей качества функционирования систем управления, основанная на применении неравенства Чебышёва-Куриленко [1], предполагает определение векторов математического ожидания и дисперсии переменных стационарного стохастического уравнения состояний
, (31)
Причем, если при рассмотрении собственного движения их вычисление особых проблем не возникает, то вынужденное движение для чистоты результата требует разделения стохастического оператора 
и вектора 
, который может содержать случайные составляющие. При этом информацию о наличии случайных параметров в самой матрице желательно сохранить.
Покажем возможность такого разделения.
Рассмотрим вначале соответствующее (31) детерминированное уравнение состояния
(32)
или в скалярной форме:
(33)
Добавим в (33) 
входов:
(34)
Если в (34) при любых значениях коэффициентов 
элементы вектора управления 
торжественно равны нулю, то (34) переходит к (33).
Перепишем (34) в матричной форме:
(35)
где 
– квадратная матрица размерности 
; 
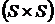– вектор управления размерности 
, имеющий последние 
элементы, равные нулю.
Проблему выбора значений коэффициентов 
рассмотрим позднее.
Матрица должна быть невырожденной и иметь обратную матрицу 
. Тогда умножая (35) слева на матрицу , получим
(36)
Произведя замену переменной 
и 
получим
(37)
где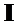 
– единичная матрица и 
.
При переходе к стохастическому виду, т.е. к уравнению (31), и производя аналогичные преобразования, получим
(38)
где 
.
Таким образом, в уравнении (10) у вектора внешних переменных 
не содержится стохастического оператора. И, в то же время, информация о стохастичности вектора (матрицы) коэффициентов усиления 
уравнения (31) не потеряна, так как вошла в матрицу свободного движения 
уравнения (38).
При достаточно произвольном выборе дополнительных элементов вектора (матрицы) 
(35) необходимо соблюсти следующие условия:
- все их значения должны и могут быть детерминированными;
- матрица должна быть невырожденной, т.е. должна существовать обратная матрица 
;
- число обусловленности матрицы , как известно [3], [4], [7] должно быть минимальным (по крайней мере, равным числу обусловленности матрицы 
уравнения (32)). Отметим, что для уравнения (31) при расширении матрицы 
следует использовать математические ожидания её элементов.
Остановимся на последнем условии подробнее.
Известно [3], что число обусловленности характеризует меру близости матрицы 
к вырожденной матрице.
Оно определяется выражением
,
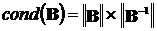где 
, 
– нормы соответствующих матриц.
Причём для любой матрицы, число обусловленности должно быть не менее 1 и если оно больше 10, то матрица является плохо обусловленной. Число обусловленности матрицы может быть рассчитано через сингулярные значения и соответствующие им унитарные векторы.
Для прямоугольной матрицы , сингулярным значением называется неотрицательная скалярная величина 
, удовлетворяющая условию:
(39)
где 
и 
соответствующая этому сингулярному значению пара векторов-столбцов.
Если матрица имеет несколько сингулярных значений, образующих диагональную матрицу 
, то матрицы 
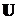и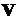 
являются унитарными (в случае, если матрица вещественная – ортогональными) и выражения (39) принимают вид:
(40)
откуда следует:
. (41)
В случае спектральной нормы число обусловленности матрицы равно отношению её максимального сингулярного значения к минимальному:
, (42)
Поэтому число обусловленности матрицы, имеющей одинаковые отличные от нуля сингулярные значения всегда равно единице.
Покажем, что с помощью (42) с учетом (40) и (41) при выборе дополнительных элементов вектора (матрицы) (35) можно решить задачу минимизации ее числа обусловленности.
Пусть имеется исходная прямоугольная матрица 
размерности 
:
. (43)
Осуществляя расширение размерности до размерности 
добавлением матрицы 
с размерностью 
, (44)
получим расширенную квадратную матрицу 
(45)
Если представить (43) и (44) в виде квадратных матриц с добавлением дополнительных 
и 
нулевых векторов-столбцов, то можно получить:
, 
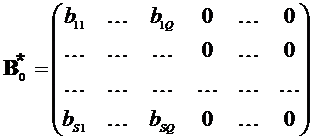(46)
и тогда (45) запишется следующим образом:
. (47)
Из (41) следует, что
. (48)
С учетом (47)
. (49)
Отметим, что для пары векторов 
(47) и 
(45), а также для 
(48) и (47), значения ненулевых диагональных элементов матриц 
и 
(
и 
), определяемых по (40) остаются неизменными.
Как правило, элементы диагональных матриц сингулярных значений в (21) должны располагаться в нарастающем порядке. Поэтому выражение 
следует понимать не как сумму матриц, а как добавление диагональных матриц друг к другу таким образом, чтобы элементы полученной диагональной матрицы 
также располагались в нарастающем порядке.
Таким образом, число обусловленности матрицы не изменится, если к ней добавить особо выборочное ограниченное число ненулевых векторов-столбцов».
Если исходная прямоугольная матрица имеет соответствующую диагональную матрицу сингулярных значений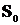 
и число обусловленности 
, то и матрица имеет диагональную матрицу и число обусловленности 
.
Из (21) видно, что расширенная матрица имеет наименьшее число обусловленности (возможно равное числу обусловленности матрицы 
) только тогда, когда 
и 
. Поэтому, для того, чтобы число обусловленности расширенной матрицы было равно числу обусловленности исходной матрицы, необходимо выбрать элементы матрицы таким образом, чтобы ее сингулярные значения находились в интервале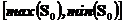 
.
Рассмотрим частный случай, когда число обусловленности матрицы равно единице, то есть она имеет одинаковые сингулярные значения 
, которые для простоты можно выбрать 
или 
. В этом случае, все элементы векторов-столбцов матрицы В1, определяемой по (16) торжественны нулям, кроме одного, равного выбранному сингулярному значению благодаря тому, что матрицы U и V являются унитарными (при вещественных матрицах - ортогональными).
Пример
Пусть функционирование (продольное движение) пассажирского судна на подводных крыльях описывается линеаризованным стационарным уравнением состояний в матричной форме [2]:
(50)
где 
, 
– угол дифферента (тангажа) и его производная;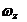 
, 
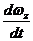– угловая скорость килевой качки и ее производная; 
, 
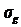– ордината центра масс судна и ее производная; 
, 
– угол атаки и его производная; 
, 
– углы поворота носовых и кормовых крыльев (управляющие воздействия); 
– коэффициенты, зависящие от конструкции судна.
Напомним, что эти коэффициенты являются регулярными функциями от случайных 
- параметров и на практике рассчитываются и задаются их математическими ожиданиями. Например, для судна водоизмещением 60т матрицы 
и 
имеют следующие значения своих элементов:
В данном примере, исходная матрица 
имеет размерность 4х2. Используя стандартную программу определения числа обусловленности в среде Matlab (см. приложение) [6], найдем число обусловленности 
, и диагональную матрицу сингулярных значений:
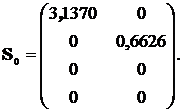(51)
Выбираем ненулевой элемент равным максимальному сингулярному значению (в данном случае 3,1370) и составим дополнительную матрицу В1 размерностью 4х2
(52)
Тогда (46) принимают
; 
(53)
Обратить внимание на то, что все элементы первой и третьей строк исходной матрицы торжественно равны нулю, то элементы первой и третьей матрицы 
должны отличаться от нуля, иначе матрица
(54)
будет вырожденной и не существует ей обратной.
Матрицы в (5224), (5325) и (5426) имеют соответствующие матрицы сингулярных значений:
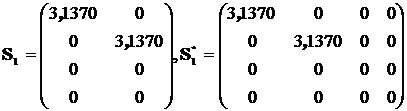
(55)
Последнее выражение показывает, что число обусловленности расширенной матрицы В по (42) остается тем же, равным исходной = 4,7344. Соответствующая обратная ей матрица определится в виде:
.
Осуществляя преобразования (37) и (38), получим новую матрицу 
, элементы которой при переходе к стохастическому виду также являются регулярными функциям от случайных 
- параметров системы:
.
В рассматриваемом примере, ее математическое ожидание имеет вид:
.
В результате чего (38) примет вид:
. (56)
Таким образом, исследование влияния случайных - параметров на переменные состояния исходной системы, проведенное по уравнению (30), несомненно, дает более достоверный и полный результат, так как составляющие матрицы 
содержат информации не только первоначальной матрицы 
уравнения (3), но и матрицы 
.
Следующий шаг – применение интервальных вычислений [8] для определения нижней и верхней границ собственных значений фундаментальной матрицы системы без учета (3) и при учете (30) стохастичности элементов исходной матрицы В.
Согласно [9], при малых вариациях элементов матрицу А можно представить в виде интервальной матрицы 
. Следовательно, если пренебречь малыми изменениями собственных векторов Н (считая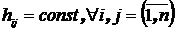 
), то собственные значения интервальной матрицы 
также будут интервальными, то есть 
. Для интервальных собственных значений справедливы следующие выражения:
(57)
Если предполагать, что случайные параметры элементов системы имеют равномерное распределение в заданных границах (интервалах), то при ее производстве и эксплуатации они «переходят» к усеченному нормальному закону распределения показателей качества функционирования [10]. Тогда, с учетом (57) и «правила трех сигм» математические ожидания и дисперсии собственных значений будут
(58)
При математическом моделировании (см. приложение) для рассмотренного примера разбросы элементов фундаментальной матрицы А выбраны для двух варианта: 
и 
, а для элементов матрицы В соответственно 
и 
.
Были получены значения математических ожиданий и дисперсий собственных значений (согласно формуле (58)):
1- При первом варианте и без учета разбросов элементов матрицы В:
.
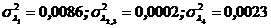2- При втором варианте 
и без учета разбросов элементов матрицы В:
Таким образом, при больших разбросах значения математических ожиданий собственных значений системы остаются неизмененными, а дисперсии увеличиваются, следовательно, вероятностная оценка качества функционирования согласно [1] уменьшаются.
3- При первом варианте и учтены разбросы элементов матрицы В ( ):
.
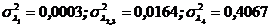4. При втором варианте и учтены разбросы элементов матрицы В ( ):
5. При втором варианте и учтены разбросы элементов матрицы В ( 
):
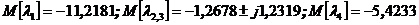
При этом верхняя граница значений собственных значений системы:
и нижняя граница:
Наличие положительно вещественных частей у собственных значений в граничных случаях свидетельствует факт потери устойчивости. Это вполне логично на практике.