ЛАБОРАТОРНАЯ РАБОТА
Вычисление сумм и произведений. Вычисление пределов. Дифференцирование и интегрирование функций. Работа с матрицами и векторами. Комплексные числа.
Оглавление
Цель работы.. 1
Вычисление сумм и произведений. 1
Разложение в ряд Тейлора. 2
Вычисление пределов. 3
Вычисление производных. 4
Исследование функций. 5
Интегрирование функции одной переменной. 7
Интегральное исчисление функций многих переменных. 8
Действия с матрицами. 9
Комплексные числа. 13
Аналитическое решение дифференциальных уравнений. 14
Контрольные задания. 18
Цель работы
Целью лабораторной работы №2 является освоить технологию вычиcленияконечных и бесконечных сумм и произведений с помощью встроенных функций sum() и product(), пределов функций и числовых последовательностей с помощью встроенной функции limit, дифференцирования и интегрирования функций, работы с матрицами и векторами, комплексными числами, дифференциальными уравнениями в программеMaple.
Вычисление сумм и произведений
Для выполнения операции суммирования в Maple используется функцияsum(f,k=m..n), в которой f – выражение, зависящее от переменной суммирования k, mи n – пределы суммирования. Пределы суммирования могут быть как конечными, так и бесконечными, т.е. функция sum() может быть использована для суммирования рядов.
Например, нам необходимо найти сумму
>sum(2^n*(n+1)/n!, n=0..20)
>evalf(%)
22.16716830
Вычислим сумму ряда
> sum(n/(n+1)!, n=0..infinity)
Вычислим сумму ряда
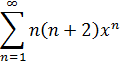
cпеременнойx.
>sum(n*(n+2)*x^n, n=1..infinity)
Функция product(), выполняющая операцию умножения, аналогична функции sum(). Аргументы функции product(f, k=m..n) следующие: f – выражение, зависящее от индекса kи являющееся k-ым членом умножения, mи n – интервал изменения k.
Например, докажем что
>product(1-1/n^2, n=2..infinity)
Разложение в ряд Тейлора
Разложение функции f (x) в степенной ряд в окрестности точки а
осуществляется командой series(f(x), x=a, n), где а – точка, в окрестности которой производится разложение, n – число членов ряда.
Аналогичного действия команда taylor(f(x), x=a, n) раскладывает функции f(x) в окрестности точки x=a до порядка n -1 по формуле Тейлора.
Команды series и taylor выдают результат, имеющий тип series. Для того, чтобы иметь возможность дальнейшей работы с полученным разложением, его следует преобразовать в полином с помощью команды convert(%,polynom).
Функцию многих переменных f (x 1,…, xn) можно разложить в ряд Тейлора по набору переменных (x 1,…, xn) в окрестности точки (a 1,…, an) до порядка n с помощью команды mtaylor(f(x), [x1,…,xn], n). Эта команда находится в стандартной библиотеке, поэтому перед использованием должна быть вызвана readlib(mtaylor).
Пример. Разложить в степенной ряд 
в окрестности х 0=0, удерживая 5 первых членов.
> f(x)=series(exp(-x)*sqrt(x+1), x=0, 5);
Разложить 
в ряд Тейлора в окрестности точки (0, 0) до 6-ого порядка.
> readlib(mtaylor):
> f=mtaylor(sin(x^2+y^2), [x=0,y=0], 7);
Вычисление пределов
В Maple для некоторых математических операций существует по две команды: одна прямого, а другая – отложенного исполнения. Имена команд состоят из одинаковых букв за исключением первой: команды прямого исполнения начинаются со строчной буквы, а команды отложенного исполнения – с заглавной. После обращения к команде отложенного действия математические операции (интеграл, предел, производная и т.д.) выводятся на экран в виде стандартной аналитической записи этой операции. Вычисление в этом случае сразу не производится. Команда прямого исполнения выдает результат сразу.
Для вычисления пределов имеются две команды:
1) прямого исполнения – limit(expr,x=a,par), где expr – выражение, предел которого следует найти, a – значение точки, для которой вычисляется предел, par – необязательный параметр для поиска односторонних пределов (left – слева, right – справа) или указание типа переменной (real – действительная, complex – комплексная).
2) отложенного исполнения – Limit(expr,x=a,par), где параметры команды такие же, как и в предыдущем случае. Пример действий этих команд:
> Limit(sin(2*x)/x,x=0);
> limit(sin(2*x)/x,x=0);
С помощью этих двух команд принято записывать математические выкладки в стандартном аналитическом виде, например:
> Limit(x*(Pi/2+arctan(x)),x=-infinity)= limit(x*(Pi/2+arctan(x)), x=-infinity);
Односторонние пределы вычисляются с указанием параметров: left – для нахождения предела слева и righ – справа. Например:
> Limit(1/(1+exp(1/x)),x=0,left)= limit(1/(1+exp(1/x)),x=0,left);
> Limit(1/(1+exp(1/x)),x=0,right)=limit(1/(1+exp(1/x)), x=0,right);
Вычисление производных
Для вычисления производных в Maple имеются две команды:
1) прямого исполнения – diff(f,x), где f – функция, которую следует продифференцировать, x – имя переменной, по которой производится дифференцирование.
2) отложенного исполнения – Diff(f,x), где параметры команды такие же, как и в предыдущей. Действие этой команды сводится к аналитической записи производной в виде 
. После выполнения дифференцирования, полученное выражение желательно упростить. Для этого следует использовать команды simplifyfactor или expand, в зависимости от того, в каком виде вам нужен результат.
Пример:
> Diff(sin(x^2),x)=diff(sin(x^2),x);
Для вычисления производных старших порядков следует указать в параметрах x$n, где n – порядок производной; например:
> Diff(cos(2*x)^2,x$4)=diff(cos(2*x)^2,x$4);
Полученное выражение можно упростить двумя способами:
> simplify(%);
> combine(%);
Большинство задач дифференциального исчисления функций многих переменных решается в Maple теми же командами, что и для функций одной переменной, только с указанием дополнительных параметров.
Для вычисления частных производных функции f (x 1,…, xm) используется уже хорошо известная вам команда diff. В этом случае эта команда имеет такой формат: diff(f,x1$n1,x2$n2,…, xm$nm), где x1,…, xm – переменные, по которым производится дифференцирование, а после знака $ указаны соответствующие порядки дифференцирования. Например, частная производная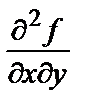 
записывается в виде: diff(f,x,y).
Найти все частные производные 2-го порядка функции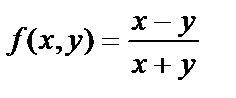 
.
> restart; f:=(x-y)/(x+y):
> Diff(f,x$2)=simplify(diff(f,x$2));
> Diff(f,y$2)=simplify(diff(f,y$2));
> Diff(f,x,y)=diff(f,x,y);
.
Исследование функций
Исследование функции необходимо начинать с нахождения ее области определения, но, к сожалению, это трудно автоматизируемая операция. Поэтому при рассмотрении этого вопроса приходится решать неравенства (см. тему II). Однако, ответить на вопрос, определена ли функция на всей числовой оси, или нет, можно исследовав ее на непрерывность.
Проверить непрерывность функции f (x) на заданном промежутке [ x 1, x 2] можно с помощью команды iscont(f,x=x1..x2). Если функция f непрерывна на этом интервале, то в поле вывода появится ответ true – (истина); если функция f не является непрерывной на этом интервале, то в поле вывода появится ответ false – (ложь). В частности, если задать интервал x=-infinity..+infinity, то функция f будет проверяться на всей числовой оси. В этом случае, если будет получен ответ true, то можно сказать, что функция определена и непрерывна на всей числовой оси. В противном случае следует искать точки разрыва. Это можно сделать двумя способами:
1) с помощью команды discont(f,x), где f – функция, исследуемая на непрерывность, x – переменная. Эта команда пригодна для нахождения точки разрыва первого и второго родов.
2) с помощью команды singular(f,x), где f – функция, x – переменная. Эта команда годится для нахождения точек разрыва второго рода как для вещественных значений переменной, так и для комплексных.
Обе эти команды выдают результаты в виде перечисления точек разрыва в фигурных скобках. Тип такой записи называется set. Для того, чтобы в дальнейшем можно было использовать полученные значения точек разрыва, следует из типа set с помощью команды convert перевести их в обычный числовой тип.
1. Найдите точки разрыва функции 
> iscont(exp(1/(x+3)),x=-infinity..+infinity);
false
Это означает, что функция не является непрерывной. Поэтому следует найти точки разрыва с помощью команды:
> discont(exp(1/(x+3)),x);
{-3}
Ответ наберите в текстовом режиме в новой строке:
“Точка разрыва x =-3.”
2. Найти точки разрыва функции 
> iscont(tan(x/(2-x)),x=-infinity..infinity);
false
> singular(tan(x/(2-x)),x);
{ x =2},{ x =2 
}
Здесь _ N – целые числа. Ответ наберите в текстовом режиме в новой строке:
“Точки разрыва: x =2 и x =2p(2 n +1)/(p(2 n +1)-2).”
В Maple для исследования функции на экстремум имеется команда extrema(f,{cond},x,’s’), где f - функция, экстремумы которой ищутся. В фигурных скобках {cond} указываются ограничения для переменной, х – имя переменной, по которой ищется экстремум, в апострофах ’s’ – указывается имя переменной, которой будет присвоена координата точки экстремума. Если оставить пустыми фигурные скобки {}, то поиск экстремумов будет производиться на всей числовой оси. Пример:
> extrema(arctan(x)-ln(1+x^2)/2,{},x,’x0’);x0;
{{ x =1}}
В первой строке вывода приводится экстремум функции, а во второй строке вывода – точка этого экстремума.
К сожалению, эта команда не может дать ответ на вопрос, какая из точек экстремума есть максимум, а какая – минимум. Для нахождения максимума функции f (x) по переменной х на интервале 
используется команда maximize(f,x,x=x1..x2), а для нахождения минимума функции f (x)по переменной х на интервале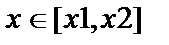 
используется команда minimize(f, x, x=x1..x2). Если после переменной указать ’infinity’ или интервал x=-infinity..+infinity, то команды maximize и minimize будут искать, соответственно, максимумы и минимумы на всей числовой оси как во множестве вещественных чисел, так и комплексных. Если такие параметры не указывать, то поиск максимумов и минимумов будет производиться только во множестве вещественных чисел. Пример:
> maximize(exp(-x^2),x);
Координаты точек максимума или минимума можно получить, если в параметрах этих команд после переменной записать через запятую новую опцию location. В результате в строке вывода после самого максимума (минимума) функции будут в фигурных скобках указаны координаты точек максимума (минимума). Например:
>minimize(x^4-x^2, x, location);
, { 
, 
}
В строке вывода получились координаты минимумов и значения функции в этих точках.
Так же, как и для функции одной переменной, наибольшее и наименьшее значения функции многих переменных вычисляются командами maximize(f,{x1,…,xn},range), и minimize(f,{x1,…,xn}, range), где следует указывать после функции в фигурных скобках список всех переменных, от которых она зависит, а затем интервалы для каждой переменной, указывающие область поиска наибольшего и наименьшего значений.
Интегрирование функции одной переменной
Неопределенный интеграл 
вычисляется с помощью 2-х команд:
1) прямого исполнения – int(f, x), где f – подынтегральная функция, x – переменная интегрирования;
2) отложенного исполнения – Int(f, x) – где параметры команды такие же, как и в команде прямого исполнения int. Команда Int выдает на экран интеграл в аналитическом виде математической формулы.
Для вычисления определенного интеграла 
в командах int и Int добавляются пределы интегрирования, например,
> Int((1+cos(x))^2, x=0..Pi)=int((1+cos(x))^2, x=0..Pi);
Если в команде интегрирования добавить опцию continuous: int(f, x, continuous), то Maple будет игнорировать любые возможные разрывы подынтегральной функции в диапазоне интегрирования. Это позволяет вычислять несобственные интегралы от неограниченных функций. Несобственные интегралы с бесконечными пределами интегрирования вычисляются, если в параметрах команды int указывать, например, x=0..+infinity.
Если требуется вычислить интеграл, зависящий от параметра, то его значение может зависеть от знака этого параметра или каких-либо других ограничений. Рассмотрим в качестве примера интеграл 
, который, как известно из математического анализа, сходится при а >0 и расходится при а <0. Если вычислить его сразу, то получится:
>Int(exp(-a*x),x=0..+infinity)=int(exp(-a*x),x=0..+infinity);
Для получения явного аналитического результата вычислений следует сделать какие-либо предположения о значении параметров, то есть наложить на них ограничения. Это можно сделать при помощи команды assume(expr1), где expr1 – неравенство. Дополнительные ограничения вводятся с помощью команды additionally(expr2), где expr2 – другое неравенство, ограничивающее значение параметра с другой стороны.
Вернемся к вычислению интеграла с параметром 
, которое следует производить в таком порядке:
>assume(a>0);
>Int(exp(-a*x),x=0..+infinity)=int(exp(-a*x),x=0..+infinity);
