Министерство здравоохранения РФ
Кировская государственная медицинская академия
Кафедра медицинской и биологической физики
Основы теории
вероятностей
и математической
статистики
Вопросы тестового контроля
знаний студентов первого курса
лечебного и педиатрического факультетов
Киров – 2003
Основы теории вероятностей и математической статистики.
Вопросы тестового контроля знаний студентов первого курса лечебного и педиатрического факультетов.
Составители: О. Л. Короткова, В. А. Кудрявцев, Е. В. Луценко, П. Г. Чупраков, О. И. Шилов. Под редакцией зав. кафедрой медбиофизики КГМА к. ф.-м. н., доц. В. А. Кудрявцева.
Технический редактор, подготовка оригинал-макета, набор и вёрстка, разработка компьютерной версии теста – О. И. Шилов.
Корректор – Е. Р. Клабукова.
© 1995–2003, кафедра медбиофизики КГМА
© 2003, О. И. Шилов, компьютерная версия теста
Все права защищены. Несанкционированное копирование и распространение любыми способами полностью или частично запрещено.
Основы теории вероятностей
и математической статистики
Правильные утверждения помечены символом þ.
1. Событие, которое в данных условиях может произойти или не произойти, называется случайным. þ
2. Случайное событие – это событие, которое может не произойти, если изменятся условия опыта.
3. Случайное событие – это такое событие, которое зависит от случая.
4. Случайное событие называется достоверным, если оно может произойти или не произойти в данных условиях.
5. Случайное событие называется достоверным, если в результате данного испытания оно обязательно происходит. þ
6. Случайное событие называется достоверным, если в результате данного испытания оно обязательно не происходит.
7. Случайное событие называется невозможным, если в данных условиях оно может произойти или не произойти.
8. Случайное событие, которое в данных условиях произойти не может, называется невозможным. þ
9. Примером невозможного события может служить событие: вынуть чёрный шар из урны, в которой имеются в основном белые шары и некоторое количество чёрных.
10. Примером невозможного события может служить событие: вынуть красный шар из урны, в которой имеются чёрные и белые шары. þ
11. Два события называются совместными, если вероятность появления одного из них зависит от того, произошло или не произошло второе.
12. Два события называются совместными, если появление одного из них не исключает появление другого. þ
13. Примером совместных событий может служить событие: одновременное выпадение герба и решки при бросании двух монет. þ
14. Если событие А – выпадение цифры 5 при бросании игральной кости, а событие В – выпадение цифры 3, то событие В является противоположным событию А: 
15. События А и В называются противоположными, если появление события А исключает появление события В.
16. Событие В, происходящее тогда и только тогда, когда не происходит событие А, называется противоположным событию А: 
þ
17. Два события А и В называются несовместными, если при появлении одного из них не всегда происходит другое.
18. Два события А и В называются несовместными, если появление одного из них исключает появление другого. þ
19. Событие B, происходящее, когда может не произойти событие A, называется противоположным последнему.
20. События А1; А2; А3; …; Аn образуют полную группу событий, если события Аi попарно несовместны и равновозможны.
21. События А1; А2; А3; …; Аn образуют полную группу событий, если они попарно несовместны и единственно возможны. þ
22. Размещением из n элементов по m элементов называется упорядоченное подмножество, состоящее из m различных элементов данного множества: þ
23. Размещения отличаются или составом элементов или порядком их следования. þ
24. Размещения отличаются или составом элементов или их количеством.
25. Размещением из n элементов по m элементов называется любое подмножество, состоящее из m различных элементов данного множества.
26. Перестановкой из n элементов называется размещение из n элементов по n элементов
þ
27. Перестановки отличаются порядком следования элементов в подмножестве. þ
28. Перестановки отличаются количеством элементов и порядком их следования.
29. Сочетанием из n элементов по m элементов называется любое подмножество, которое содержит m различных элементов данного множества:
þ
30. Сочетания отличаются составом и порядком следования элементов.
31. Сочетания отличаются только составом элементов. þ
32. В множестве из n элементов можно сделать больше размещений по m элементов 
, чем сочетаний 
þ.
33. В множестве из n элементов можно сделать больше сочетаний по m элементов , чем размещений
34. Вероятностью события А называется отношение общего числа элементарных событий к числу случаев, в которых произошло событие А.
35. Вероятностью события А называется отношение числа m элементарных событий, благоприятствующих появлению события А к общему числу всех возможных элементарных исходов n. þ
36. Под вероятностью события А, в статистическом смысле, понимают почти достоверный предел, к которому стремится относительная частота появления события А при неограниченном числе появлений события А:
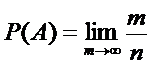
37. Под вероятностью события А, в статистическом смысле, понимают почти достоверный предел, к которому стремится относительная частота появления события А при неограниченном числе испытаний:
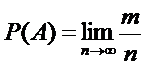þ
38. События А и В называются зависимыми, если при проведении испытаний вероятности их изменяются.
39. Событие А называется зависимым от события В, если вероятность наступления события В зависит от того, наступило или нет событие А. þ
40. Суммой событий А и В называют событие С, заключающееся в том, что в результате испытаний наступит или событие А, или событие В, или они наступят оба. þ
41. Суммой событий А и В называют событие С, заключающееся в том, что в результате испытаний может наступить одно из этих событий.
42. Суммой событий А и В называют событие С, заключающееся в том, что наступят и событие А, и событие В одновременно.
43. Произведением событий А и В называется событие С, заключающееся в том, что и событие А, и событие В произойдут одновременно. þ
44. Произведением событий А и В называется событие С, заключающееся в том, что и событие А, и событие В могут произойти одновременно.
45. Произведением событий А и В называется событие С, заключающееся в том, что или событие А, или событие В обязательно произойдут.
46. Произведением событий А, В и С называется событие, заключающееся в том, что хотя бы два из этих событий произойдут одновременно.
47. Вероятность наступления хотя бы одного из двух несовместных событий А и В равна сумме вероятностей этих событий: Р(АВ)=Р(А)+Р(В)
48. Вероятность наступления хотя бы одного из двух несовместных событий, безразлично которого, равна сумме их вероятностей: Р(А или В)=Р(А)+Р(В) þ
49. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий, умноженной на вероятность их совместного появления: Р(А или В)=(Р(А)+Р(В)).Р(АВ)
50. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления: Р(А+В)=Р(А)+Р(В)-Р(АВ). þ
51. Вероятность появления хотя бы одного из двух несовместных событий равна сумме вероятностей этих событий, без вероятности их совместного появления: Р(А+В)=Р(А)+Р(В)-Р(АВ)
52. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий и вероятности их совместного появления: Р(А+В)=Р(А)+Р(В)+Р(АВ)
53. Вероятность совместного появления двух зависимых событий или А, или В равна сумме вероятностей этих событий: Р(А или В)=Р(А)+Р(В)
54. Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого: Р(АВ)=Р(А).РA(В) þ
55. Вероятность совместного появления двух и более независимых случайных событий А и В определяется произведением вероятностей этих событий:
Р(А и В)=Р(А).Р(В) þ
56. Вероятность совместного появления двух и более независимых случайных событий A или B определяется произведением вероятностей этих событий:
Р(А или В)=Р(А).Р(В)
57. Для зависимых событий справедливо следующее выражение:
þ
58. Вероятность произведения двух или более независимых событий равна произведению вероятностей этих событий. þ
59. Вероятность произведения двух или более независимых событий равна произведению вероятностей этих событий на их условную вероятность.
60. Для зависимых событий справедливо следующее выражение:
Р(АВС)=Р(АВ)+Р(АС)+Р(ВС)
61. Условная вероятность – это вероятность зависимого события.
62. Условная вероятность – это вероятность события В при условии, что произошло событие А. þ
63. Условная вероятность – это вероятность события А, заключающегося в том, что событие В может произойти или не произойти.
64. Полная вероятность события A может быть представлена следующим выражением: P(A)=P(A1).P(A2).P(A3).….P(An)
65. Полная вероятность события A может быть представлена следующим выражением: P(A)=P(A1)+P(A2)+P(A3)+…+P(An)
66. Полная вероятность события A может быть представлена следующим выражением:
þ
67. Полная вероятность события A может быть представлена следующим выражением:
68. Полная вероятность события А – это вероятность события А, которое может произойти тогда и только тогда, когда осуществится хотя бы одна из несовместных гипотез (событий): 
; 
; 
; …, 
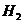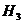, образующих полную группу событий, и при осуществлении которых может произойти событие А. þ
69. Полная вероятность события А – это вероятность события А, которое может произойти тогда и только тогда, когда осуществится хотя бы одна из совместных гипотез: 
; ; 
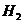; …; , образующих группу зависимых событий, при осуществлении которых может произойти событие A.
70. Полная вероятность события А – это вероятность события А при условии, что может осуществиться хотя бы одна из совместных гипотез: ; ; 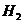; …; , при осуществлении которых может произойти событие А.
71. Полная вероятность события А – это вероятность события А при условии, что может осуществиться хотя бы одна из совместных гипотез: ; ; 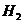; …; , при осуществлении которых может произойти событие А.
72. Для произведения вероятностей справедливо выражение: Р(АВ)=Р(ВА) þ
73. Для произведения вероятностей зависимых событий справедливо выражение: P(AB)=P(A).P(B)–P(AB)
74. Для произведения вероятностей зависимых событий справедливо выражение: 
þ
75. Для произведения вероятностей независимых событий справедливо выражение: 
76. Теоремы суммы и произведения вероятностей случайных событий можно распространить на любое конечное число событий. þ
77. Вероятность осуществления хотя бы одного из случайных событий 
; 
; 
; …; 
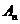, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий:
þ
78. Вероятность осуществления хотя бы одного из случайных событий ; ; ; …; 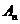, независимых в совокупности, равна разности между единицей и произведением вероятностей этих событий:
79. Вероятность одновременного наступления двух зависимых событий H и A равна произведению вероятностей этих событий и может быть найдена по формуле:
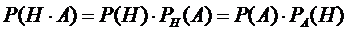þ
80. Теорема гипотез (формула Бейеса) позволяет уточнить априорную вероятность гипотез ; ; 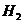; …; на основании опыта. þ
81. Выражение
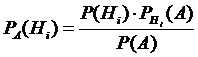
(где A – событие, которое может произойти тогда и только тогда, когда осуществится хотя бы одна из несовместных гипотез 
), является формулой Бейеса. þ
82. Выражение
(где А – событие, которое может произойти тогда и только тогда, когда осуществится хотя бы одна из несовместных гипотез ), является формулой Бейеса.
83. Выражение
(где А – событие, которое может произойти тогда и только тогда, когда осуществится хотя бы одна из несовместных гипотез ), является формулой Бейеса.
84. Формула Бернулли позволяет найти вероятность того, что при n независимых испытаниях событие А может наступить ровно m раз. þ
85. Формула Бернулли может быть представлена выражением вида:
þ
86. Формула Бернулли может быть представлена выражением вида:
87. Формула Бернулли может быть использована для расчёта вероятности того, что при n независимых испытаниях событие А наступит m раз, если выполняется схема Бернулли:
1. Число испытаний n конечно;
2. Каждое испытание имеет только два исхода: либо А, либо не А;
3. Испытания независимые;
4. Вероятность появления события А в каждом испытании постоянна. þ
88. Формула Бернулли позволяет найти вероятность того, что при n независимых испытаниях по схеме Бернулли событие А наступит ровно m раз. þ
89. Формула Бернулли может быть использована для определения вероятности наступления события А, если выполняется схема Бернулли:
1. Число испытаний n конечно;
2. Каждое испытание имеет только два исхода: либо А, либо не А;
3. Испытания независимые;
4. Вероятность появления события А в каждом испытании постоянна.
90. Формула Бернулли может быть использована для расчёта вероятности того, что при n независимых испытаниях событие А наступит m раз, если выполняется схема Бернулли:
1. Число испытаний n бесконечно;
2. Испытания независимые;
3. Вероятность появления события А при каждом испытании изменяется.
91. Наивероятнейшим числом появления считается такое число появлений (по схеме Бернулли), вероятность которого наибольшая. þ
92. Схема проведения испытаний случайных событий Бернулли:
1. Число испытаний конечно;
2. Каждое испытание имеет только два исхода: либо А, либо не А;
3. Испытания независимые;
4. Вероятность появления события А в каждом испытании постоянна. þ
93. Схема проведения испытаний случайных событий Бернулли:
1. Число испытаний бесконечно велико;
2. Каждое испытание может иметь своим исходом только А;
3. Испытания независимые;
4. Вероятность появления события А в каждом испытании постоянно изменяется.
94. Величину, которая в результате испытания примет одно и только одно возможное значение (при этом заранее неизвестно, какое именно), называют случайной. þ
95. Величину, которая в результате испытания может принять заранее известное значение, называют случайной.
96. Дискретной (прерывной) называют случайную величину, принимающую отдельные друг от друга возможные значения с опредёленными вероятностями, которые можно пронумеровать. þ
97. Непрерывной называют случайную величину, принимающую любые значения в некотором интервале с заданной вероятностью. þ
98. Непрерывной называют случайную величину, принимающую только отдельные значения в некотором интервале с заданной вероятностью.
99. В качестве примера дискретной случайной величины можно использовать результаты измерения роста студентов в группе или на курсе.
100. В качестве примера непрерывной случайной величины можно использовать результаты измерения роста студентов в группе или на курсе. þ
101. В качестве примера непрерывной случайной величины можно использовать результаты бесконечно большого числа бросаний игральной кости.
102. Непрерывная величина считается заданной, если известна её функция распределения. þ
103. Случайная величина, принимающая только целые значения с определёнными вероятностями, называется дискретной.
104. Случайную величину, вероятность которой принимает любые значения из интервала от 0 до 1, называют непрерывной.
105. Дискретная величина считается заданной, если перечислены все её возможные значения.
106. Дискретная величина считается заданной, если известен её закон распределения. þ
107. Для дискретной случайной величины закон распределения может быть задан в виде бесконечной таблицы.
108. К числовым характеристикам дискретной случайной величины относят среднее арифметическое и доверительный интервал.
109. Графическое изображение ряда распределения называют полигоном частот. þ
110. Законом распределения дискретной случайной величины называют ряд значений случайной величины, расположенных в порядке возрастания.
111. Законом распределения дискретной случайной величины называют ряд значений случайной величины, включающий все возможные значения этой случайной величины.
112. Законом распределения дискретной случайной величины называют соответствие между её возможными значениями и их вероятностями. þ
113. Закон распределения дискретной случайной величины может быть задан в виде таблицы, в которую включены значения случайной величины и соответствующие им вероятности: þ
| X | x1 | x2 | x3 | x4 | x5 | x6 | x7 | ... | xi | ... | xn-1 | xn |
| P | p1 | p2 | p3 | p4 | p5 | p6 | p7 | ... | pi | ... | pn-1 | pn |
114. Закон распределения непрерывной случайной величины может быть задан в виде таблицы, в которую включены значения случайной величины и соответствующие им вероятности:
| X | x1 | x2 | x3 | x4 | x5 | x6 | x7 | ... | xi | ... | xn-1 | xn |
| P | p1 | p2 | p3 | p4 | p5 | p6 | p7 | ... | pi | ... | pn-1 | pn |
115. Закон распределения дискретной случайной величины может быть задан в виде функциональной зависимости между плотностью вероятности случайной величины и её значениями.
116. Закон распределения дискретной случайной величины может быть задан в виде:
þ
117. Закон распределения дискретной случайной величины может быть задан в виде:
118. Закон распределения дискретной случайной величины может быть задан в виде таблицы, в которую включены значения случайной величины и соответствующие им математические ожидания:
| X | x1 | x2 | x3 | x4 | x5 | x6 | x7 | ... | xi | ... | xn-1 | xn |
| М | М 1 | М 2 | М 3 | М 4 | М 5 | М 6 | М 7 | ... | М i | ... | М n-1 | М n |
119. Случайную величину будем называть непрерывной, если все её возможные значения целиком заполняют некоторый конечный или бесконечный промежуток. þ
120. К числовым характеристикам дискретной случайной величины относятся: математическое ожидание; дисперсия; среднее квадратическое отклонение; мода; медиана. þ
121. К числовым характеристикам дискретной случайной величины относятся: математическое ожидание; вероятность появления случайной величины; закон распределения; мода; медиана.
122. Математическим ожиданием М(Х) дискретной случайной величины Х называется сумма произведений всех возможных значений случайной величины на соответствующие вероятности. þ
123. Математическое ожидание дискретной случайной величины может быть представлено выражением:
þ
124. Математическим ожиданием М(Х) дискретной случайной величины Х называется произведение значения случайной величины на её вероятность.
125. При большом числе испытаний среднее арифметическое дискретной случайной величины близко к её математическому ожиданию. þ
126. Математическое ожидание приближённо равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины. þ
127. Математическое ожидание приближённо равно (тем точнее, чем больше число испытаний) дисперсии наблюдаемых значений случайной величины.
128. Математическое ожидание постоянной величины С равно этой постоянной: М(С)=С þ
129. Математическое ожидание постоянной величины С равно произведению вероятности на её значение.
130. Математическое ожидание алгебраической суммы(разности) случайных величин равно сумме их математических ожиданий:
131. Математическое ожидание алгебраической суммы (разности) случайных величин равно сумме (разности) их математических ожиданий:
þ
132. Математическое ожидание произведения независимых случайных величин равно сумме их математических ожиданий:
133. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:
þ
134. Модой 
дискретного распределения называют такое значение 
дискретной случайной величины, которое имеет наибольшую вероятность. þ
135. Модой 
дискретного распределения называют такое значение 
дискретной случайной величины, которое расположено в центре ряда распределения.
136. Медианой Me дискретного распределения называют такое значение xm дискретной случайной величины, которое расположено в центре ряда распределения. þ
137.
| Х | |||||||||
| Р | 0,181 | 0,220 | 0,241 | 0,038 | 0,090 | 0,071 | 0,070 | 0,032 | 0,048 |
Mo =4
138.
| Х | |||||||||
| Р | 0,181 | 0,220 | 0,241 | 0,038 | 0,090 | 0,071 | 0,070 | 0,032 | 0,048 |
Me =4 þ
139.
| Х | |||||||||
| Р | 0,181 | 0,220 | 0,241 | 0,038 | 0,090 | 0,071 | 0,070 | 0,032 | 0,048 |
Mo =2 þ
140. Дисперсией дискретной случайной величины называют математическое ожидание квадрата отклонения этой случайной величины от её математического ожидания. þ
141. Дисперсия дискретной случайной величины может быть представлена выражением:
142. Дисперсия дискретной случайной величины может быть представлена выражением:
þ
143. Дисперсия дискретной случайной величины может быть представлена выражением:
144. Дисперсия случайной величины характеризует математическое ожидание дискретной случайной величины.
145. Дисперсия случайной величины характеризует математическое ожидание отклонений дискретной случайной величины от её среднего или математического ожидания.
146. Дисперсия суммы (разности) дискретных случайных величин равна сумме (разности) дисперсий этих случайных величин.
147. Дисперсия суммы (разности) дискретных случайных величин равна сумме дисперсий этих случайных величин. þ
148. Дисперсия суммы (разности) дискретных случайных величин равна произведению дисперсий этих случайных величин.
149. Средним квадратическим отклонением случайной величины называется корень квадратный из дисперсии. þ
150. Среднее квадратическое отклонение n дискретных случайных величин может быть представлено выражением:
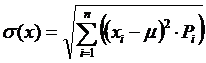þ
151. Среднее квадратическое отклонение n случайных величин может быть представлено выражением:
152. Среднее арифметическое одинаково распределённых, имеющих одинаковые математические ожидания 
, независимых случайных величин 
, 
, …, 
, имеет такое же математическое ожидание, как и каждая из них – . þ
153. Среднее арифметическое одинаково распределённых, имеющих одинаковые математические ожидания 
, независимых случайных величин , , …, , имеет математическое ожидание, равное 
.
154. Дисперсия среднего арифметического 
одинаково распределённых, имеющих одинаковые дисперсии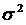 
независимых случайных величин 
, 
, …, 
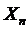обратно пропорциональна их числу:
þ
155. Дисперсия среднего арифметического 
одинаково распределённых, имеющих одинаковые дисперсии 
независимых случайных величин 
, 
, …, 
пропорциональна их числу:
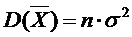
156. Закон распределения непрерывной случайной величины можно описать при помощи таблицы.
157. Функцией распределения случайной величины Х, называется функция F(x), равная вероятности того, что случайная величина приняла значение меньшее х:
þ
158. Функцией распределения случайной величины Х, называется функция F(x), равная вероятности того, что случайная величина приняла наперёд заданное значение, равное x:
159. Геометрически равенство F(x)=P(Х<x) можно толковать так: F(x) - есть вероятность того, что появившееся в результате опыта значение случайной величины Х будет лежать левее точки х на числовой оси ОХ. þ
160. Вероятность попадания случайной величины Х в промежуток (a, b) равна разности между значениями функции распределения на правом и левом концах промежутка: Р(а<X<b)=F(b)-F(a) þ
161. Вероятность попадания случайной величины Х в промежуток (a, b) равна значению функции распределения на правом конце промежутка.
162. Вероятность того, что непрерывная случайная величина примет свои значения на некотором промежутке, обратно пропорциональна ширине этого промежутка.
163. Вероятность того, что непрерывная случайная величина примет свои значения на некотором промежутке, пропорциональна ширине этого промежутка. þ
164. Вероятность того, что дискретная случайная величина примет какое-либо наперёд заданное значение, равна нулю.
165. Вероятность того, что непрерывная случайная величина примет какое-либо наперёд заданное значение, равна нулю. þ
166. Плотностью распределения вероятностей непрерывной случайной величины X называют функцию f(x) – первую производную от функции распределения F(x):
þ
167. Плотностью распределения вероятностей непрерывной случайной величины X называют функцию f(x) – первообразную от функции распределения F(x):
168. Вероятность того, что непрерывная случайная величина примет свои значения на некотором промежутке dx, может быть представлена выражением:
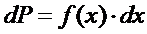þ
169. Вероятность того, что непрерывная случайная величина примет свои значения на некотором промежутке dx, может быть представлена выражением:
170. Вероятность попадания случайной величины Х в промежуток (а, b) равна разности между значениями функции распределения на правом и левом концах промежутка: Р(а<Х<b)=F(b)+F(а)
171. Закон распределения непрерывной случайной величины называют нормальным, если распределение её плотности вероятности подчиняется закону Гаусса. þ
172. Закон распределения непрерывной случайной величины называют нормальным, если распределение её плотности вероятности подчиняется закону Бернулли.
173. Закон распределения непрерывной случайной величины называют нормальным, если распределение её плотности вероятности подчиняется закону Гаусса и описывается уравнением:
þ
174. Закон распределения непрерывной случайной величины называют нормальным, если распределение её плотности вероятности подчиняется закону Гаусса и описывается уравнением:
175. Случайные величины , , …, называются одинаково распределёнными, если они имеют одинаковые законы распределения.
176. Случайные величины , , …, называются одинаково распределёнными, если они имеют одинаковые дисперсии.
177. Случайные величины , , …, называются одинаково распределёнными, если они имеют одинаковые законы распределения, равные математические ожидания и дисперсии. þ
178. Случайные величины , , …, называются одинаково распределёнными, если они имеют одинаковые математические ожидания.
179. Условие нормировки непрерывной случайной величины может быть представлено в виде выражения:
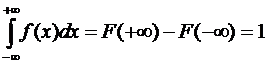þ
180. Условие нормировки непрерывной случайной величины может быть представлено в виде выражения:
181. Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат промежутку (а, b), называют величину определённого интеграла:
182. Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат промежутку (а, b), называют величину определённого интеграла:
þ
183. Математическое ожидание непрерывной случайной величины может быть представлено в виде выражения:
184. Дисперсией непрерывной случайной величины, все возможные значения которой принадлежат промежутку (а, b), называют <