Лабораторная работа 4
Тема: Построение кривых заданных уравнением в полярной системе координат и параметрическими уравнениями.
Цель: оказание студентам помощи в овладении навыками построения кривых заданных уравнением в полярной системе координат; научить студентов строить кривые заданные параметрическими уравнениями.
Теоретическое обоснование
Прямоугольная система координат  на плоскости задается двумя взаимно перпендикулярными прямыми, на каждой из которых выбрано положительное направление и задан единичный отрезок. Эти прямые называются осями координат. Положение некоторой точки
на плоскости задается двумя взаимно перпендикулярными прямыми, на каждой из которых выбрано положительное направление и задан единичный отрезок. Эти прямые называются осями координат. Положение некоторой точки  на плоскости в прямоугольной декартовой системе координат
на плоскости в прямоугольной декартовой системе координат  определяется числами
определяется числами 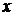 и
и  , т.е.
, т.е.  (рис.1). Эту точку можно задать и другим способом.
(рис.1). Эту точку можно задать и другим способом.
Полярная система координат задается точкой  , называемой полюсом, лучом
, называемой полюсом, лучом  , называемым полярной осью, и единичным вектором
, называемым полярной осью, и единичным вектором 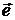 того же направления, что и луч
того же направления, что и луч  . Положение точки
. Положение точки  на плоскости определяется двумя числами: ее расстоянием
на плоскости определяется двумя числами: ее расстоянием  от полюса
от полюса  и углом
и углом  , образованным отрезком
, образованным отрезком 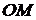 с полярной осью (рис. 2) и отсчитываемым в положительном направлении.
с полярной осью (рис. 2) и отсчитываемым в положительном направлении.

Рис. 1 Рис. 2
Числа  и
и  называются полярными координатами точки
называются полярными координатами точки  :
:  называют полярным радиусом,
называют полярным радиусом,  – полярным углом.
– полярным углом.
В определенной таким образом полярной системе координат полярный радиус  – всегда величина положительная или равная нулю (
– всегда величина положительная или равная нулю ( ), так как под
), так как под  понимается расстояние от полюса
понимается расстояние от полюса  до точки
до точки  , а расстояние, как и всякая длина, не может быть отрицательным.
, а расстояние, как и всякая длина, не может быть отрицательным.
Однако на практике удобнее пользоваться такой системой полярных координат, в которой полярный радиус  может принимать и отрицательные значения. Система полярных координат, в которой полярный радиус
может принимать и отрицательные значения. Система полярных координат, в которой полярный радиус  может принимать любые значения (положительные, отрицательные и равные нулю), называется обобщенной системой полярных координат. Этой системой мы и будем пользоваться.
может принимать любые значения (положительные, отрицательные и равные нулю), называется обобщенной системой полярных координат. Этой системой мы и будем пользоваться.
Если точка  имеет координаты
имеет координаты  и
и  :
:  , то она имеет также и координаты
, то она имеет также и координаты  и
и  ;
;  , так как угол
, так как угол  характеризует направление полярного радиуса, прямо противоположное тому, которое соответствует углу
характеризует направление полярного радиуса, прямо противоположное тому, которое соответствует углу  .
.
Отметим, что какой бы из этих двух систем полярных координат мы ни пользовались, всегда паре чисел  и
и  соответствует на плоскости единственная точка.
соответствует на плоскости единственная точка.
Если совместить полюс  с налом координат системы
с налом координат системы  , а полярную ось – с положительной полуосью
, а полярную ось – с положительной полуосью  (рис. 3), то связь между полярными и прямоугольными координатами точки устанавливается формулами:
(рис. 3), то связь между полярными и прямоугольными координатами точки устанавливается формулами:
 (1)
(1)
и
 (2)
(2)

Рис. 3
Укажем также, как следует, в полярной системе координат построить точку  по ее полярным координатам
по ее полярным координатам  и
и  . По заданному полярному углу
. По заданному полярному углу  строим ось, проходящую через полюс под углом
строим ось, проходящую через полюс под углом  к полярной оси, причем положительное направление построенной оси должно совпадать с тем направлением, которое имела бы полярная ось, если бы ее повернули против часовой стрелки на угол
к полярной оси, причем положительное направление построенной оси должно совпадать с тем направлением, которое имела бы полярная ось, если бы ее повернули против часовой стрелки на угол  . На этой оси откладываем отрезок длиной
. На этой оси откладываем отрезок длиной  от полюса
от полюса  в положительном направлении построенной оси, если
в положительном направлении построенной оси, если 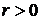 , и в отрицательном – если
, и в отрицательном – если  .
.
Уравнением линии (кривой) на плоскости  называется уравнение
называется уравнение  , которому удовлетворяют координаты
, которому удовлетворяют координаты 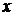 и
и  каждой точки этой линии и только они. Переменные
каждой точки этой линии и только они. Переменные 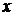 и
и  в уравнении линии называются текущими координатами точек линии.
в уравнении линии называются текущими координатами точек линии.
Аналогично вводится понятие уравнения линии в полярной системе координат:  .
.
Линию на плоскости можно задать параметрическими уравнениями:

где  – величина, называемая параметром.
– величина, называемая параметром.