Задание Д.23. Исследование свободных колебаний механической системы с одной степенью свободы

 

Определить частоту и период малых свободных колебаний механи­ческой системы с одной степенью свободы, пренебрегая силами сопро­тивления и массами нитей.

Найти уравнение движения груза 1 y — y(t), приняв за начало отсчета положение покоя груза 1 (при статической деформации пружин). Найти также амплитуду колебаний груза 1.

Схемы систем показаны на рис. 226 — 228, а необходимые данные приведены в табл. 60.

Таблица 60

 

№ вар	l	ix	ix’	r4	m1	m2	m3 m4 m5	m6	c	Начальное условие
м	кг	Н/см	y0, см	м/с
	0,5	-	-	-			-			0,1	5,0
	0,5	-	- -	0,2				3.			6,0
	0,5	3/2r	-	-		-				0,2	7,0
	0,6	-	-	-						0,2
	0,6	-	-	0,15		-					8,0
	0,6	-	-	0,15		-				0,3	7,0
	-	-	-	-		-				0,4
	-	-	-	-				-			6,0
	0,6	-	-	-			-			0,5	5,0
	0,6	-	-	-			-				6,0
	-	-	-	-			-			0,4	7,0
	0,5	-	-	-			-			0,2
	0,3	-	-	-							8,0
	0,4	-	-	0,1		-					7,0
	0,4		-	-		-				0,1
	-	-	-	-				-		0,3	6,0
	-	-	-	-			-				5,0
	-	-	-	-				-			6,0
	0,2	-	-	-			-			0,1
	0,5	-	-	-			-			0,4	7,0
	-	2r	-	-		-					8,0
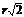
	-	-		-				-		0,1	7,0
	0,4	-	-	0,2						0,3
	-	-		-		-					6,0
	0,3	-	-	0,1						0,2	5,0
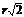
	-		-	-		-		-		0,3
	-	-	3r/2	-				-			6,0
	-	-		-				-		0,2
	-	-	4r/3	-				-			7,0
	-	-		-				-		0,3	7,0

 

В задании приняты следующие обозначения: 1 — груз массой т₁, 2 — блок массой т₂ и радиусом г₂ (сплошной однородный диск); 3 — блок массой, т₃ и радиусом инерции i_x; 4 — сплошной однородный диск массой m₄ и радиусом r₄; 5 — диск массой; m ₅ и радиусом инерции i'_x; 6 — тонкий однородный стержень массой т₆ и длиной I; 7 — стержень, масса кото­рого не учитывается; с — коэффициент жесткости пружины; у₀ — начальное отклонение груза / по вертикали от положения покоя, соответствующего статической деформации пружины; у₀ — проекция начальной скорости ₀ груза 1 на вертикальную ось.

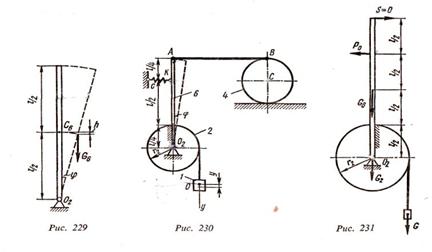
На рис. 226 — 228 системы тел 1 — 7 показаны в положении покоя (при статической деформации пружин).

В вариантах 5, 6, 14 и 23 стержень 6 жестко соединен с диском 4.

Пример выполнения задания. Дано: т₁ = 1кг, т₂=2 кг, т₄= 1 кг, т₆ = 3 кг; l = 0,6 м; с = 20 Н/см; у₀ = 0,2 см; ₀ = 8 см/с (рис. 229).

Определить циклическую частоту к и период Т малых свободных колебаний системы, а также получить уравнение у = у (t) колебаний груза 1и найти амплитуду а его колебаний.

Решение. Воспользуемся уравнением Лагранжа II рода для консер­вативной системы. Приняв за обобщенную координату системы верти­кальное отклонение у груза 1от положения покоя, соответствующего статической деформации пружины, имеем

 

где Т — кинетическая энергия системы; П — потенциальная энергия сис­темы.

Кинетическую энергию T вычислим с точностью до величин второго порядка малости относительно и у, а потенциальную энергию П — с точностью до величин второго порядка малости относительно обоб­щенной координаты у.

Найдем кинетическую энергию системы, равную сумме кинетических энергий тел 1, 2, 6 и 4:

Выразим скорость центра масс тела 4 и угловые скорости тел 2, 4 и 6 через обобщенную скорость :

v₁ = ; ω₂= /r₂; ω₆ = ω₂ = /r₂

Так как рассматриваются малые колебания, то v_B = v_A, а ввиду того, что диск 4 катится без скольжения, v_c = v_B/2; следовательно,

.

Момент инерции тела 4 относительно центральной оси

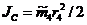
Моменты инерции тел 2 и 6 относительно оси вращения

J₂ = m₂r₂²/2; J₆ = m₆ l ²/3. Кинетическая энергия тел 1, 2, 4 и 6 имеет следующий вид:

 

Таким образом, кинетическая энергия рассматриваемой механической системы

 

Найдем потенциальную энергию системы, которая определится рабо­той сил тяжести системы и силы упругости пружины на перемещении системы из отклоненного положения, когда груз имеет координату у, в нулевое положение, которым считаем положение покоя системы:

П = П_І + П_ІІ.

Потенциальная энергия, соответствующая силам тяжести при указан-" ном перемещении,

П₁= - G₁y - G₆h,

где h — вертикальное смещение центра тяжести стержня 6, которое вы­числяем с точностью до величины второго порядка малости относительно обобщенной координаты у. По рис. 230,

h = l/2- (1/2) cos φ = (l/2) (t - cos ф).

Ограничиваясь в формуле разложения

cos φ = 1 - φ²/2! + φ⁴/4!-…

двумя первыми членами и учитывая, что

φ = y/r₂ = 4y/l

 

имеем

Таким образом,

Потенциальная энергия деформированной пружины при указанном перемещении системы равна

где - статическая деформация пружины; λ_К - перемещение точки при­крепления пружины К, соответствующее координате у. Так как (см. рис. 229)

 

т. е. = Зу, то

 

Потенциальная энергия системы

Так как в положении покоя, соответствующем статической деформации пружины,

(a)

Уравнение (а) можно получить также, составив уравнение моментов сил = 0 для положения покоя системы (рис. 231):

или

т.е.

Таким образом, потенциальная энергия рассматриваемой механической системы

Найдем значения членов уравнения (1):

 

Уравнение (1) приобретает вид

или

Обозначив к² коэффициент при у, имеем

+ к²у = 0. (2)

Циклическая частота свободных колебаний

1/с

Период свободных колебаний

Т = 2n/k = 2 • 3,14/27,1 = 0,23 с.

Интегрируя уравнение (2), получаем уравнение движения груза 1:

у = С₁ cos kt + С₂ sin kt..'

Для определения постоянных C_t и С₂ найдем уравнение скорости груза

= - kC₁ sin kt + кС₂ cos kt

и воспользуемся начальными условиями задачи. Из уравнений у = у (t) и у — y(t) при t = 0 имеем:

y₀ = C₁; = k С₂.

Следовательно,

C₁=y₀ С₂ = / k

Подставляем эти значения С_х и С₂ в уравнение y = y(t):

у = y₀ cos kt + ( /к) sin kt;

у = 0,2 cos 27,1 t + 0,3 sin 27,l t.

Уравнение у = у (t) можно получить в другом виде, если перейти к другим постоянным интегрирования αиβ, приняв

C₁=α sinβ; C₂ = αcosβ

Тогда у = a sin (kt + β), где а = , β= arctg (C₁/C₂) или

а = β = arctg (ку_о/ )

Найдем числовые значения а и β: а = 3,6 • 10 ^-2 м, β = arctg 0,68.

Так как sin β > 0 (С₁> 0), то β = 34° 12' = 0,597 рад.

Окончательно

у = 3,6 • 10^{- 2} sin (27,1t + 0,595) м.