Алгоритм расчета методом сил

Билет 3

1) N=3Д-2Ш о – С о, (1)

где Д - число неизменных жёстких частей стержневой конструкции, обладающих тремя степенями свободы;

Ш о - число простых шарниров;

С о – число опорных стержней (простых связей)

Геометрически неизменяемая система – система соединённых между собой тел (например, стержней, дисков), изменение формы которых невозможно без деформации материала. Все несущие конструкции зданий и сооружений являются неизменяемыми системами.

Геометрически изменяемая система - система, в которой возможны конечные перемещения без деформации элементов.

Мгновенно изменяемая система – система, в которой могут возникать бесконечно малые перемещения без деформации её элементов.

Мгновенно изменяемая система – в строительной механике это система с двумя стержнями, лежащими на одной оси. Такая система является геометрически изменяемой, так как её форма меняется при неизменной длине стержня. Концы двух стержней, будучи освобождёнными от наложенных связей, описывают дуги с радиусами, равными длинам стержней. Если точка крепления одного из стержней получит смещение по общей касательной этих дуг, то другой стержень не сможет воспрепятствовать этому смещению. Таким образом смещение произойдёт без деформации стержней.

Первый признак геометрической неизменяемости: ферма неизменяема, если она составлена из шарнирных треугольников поскольку треугольник неизменяемая геометрическая фигура. В данном случае к исходному треугольнику каждый последующий узел 1, 2, 3, 4 и т. д. прикрепляется двумя стержнями, вследствие чего создается новый треугольник.

Линии влияния поперечных сил в трехшарнирной арке.

Способ наложения: пусть сечение К имеет координаты , 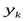и угол наклона 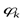. Л.в. поперечной силы в этом сечении строится на основании ее общего выражения

Значит, л.в. можно получить, построив л.в. Н и 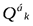и затем умножив их на соответствующие коэффициенты и сложив ординаты.

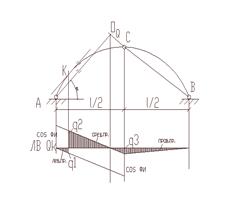
Порядок построения л.в. методом нулевых точек:

1. найти и отметить нулевую точку на линии влияния,
2. под шарниром А отложить ординату , через полученную точку и нулевую точку провести среднюю прямую (справедливую между сечением К и шарниром С),
3. параллельно средней прямой через шарнир А провести левую прямую (справедливую между опорой А и сечением К),
4. ординату средней прямой под шарниром С соединить с нулем под опорой В – правая прямая.

 

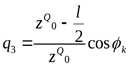
Билет 4

1) Для обеспечения геометрической неизменяемости необходимо, во-первых, чтобы связей, наложенных на перемещение узлов фермы было достаточно, во-вторых, они были правильно размещены. Следовательно, исследование геометрической неизменяемости фермы состоит из двух шагов: проверки достаточности числа связей и анализе правильности их размещения (структурном анализе фермы).

Как обычно, при анализе геометрической неизменяемости смещения, вызванные деформированием стержней в расчет не берутся. Иными словами, при анализе геометрической неизменяемости ферм, как и любых других стержневых систем, будем считать стержни абсолютно жесткими.

Каждый узел плоской фермы имеет две степени свободы, т.е. имеет возможность линейного смещения, например, в вертикальном и горизонтальном направлениях. Следовательно, минимальное количество связей, необходимых для закрепления узлов фермы от смещений, должно равняться удвоенному числу узлов. Часть из этих связей должна обеспечивать закрепление фермы относительно основания. Таким образом, минимальное число стержней в ферме, необходимое для обеспечения ее геометрической неизменяемости определяется по формуле:

где n_ст - число стержней в ферме, n_узл - число узлов, а n_оп.св - число опорных связей.

Условие (1) одновременно является условием статической определимости фермы. Действительно, для каждого узла можно составить два уравнения равновесия- условия равенства нулю проекций на вертикальную и горизонтальную оси всех действующих на узел внешних сил и сил, действующих со стороны стержней и реакций опор. Неизвестными же являются продольные усилия в каждом стержне и реакции в опорах. Записав все эти 2∙ n_узл уравнений, получим систему уравнений, которую в матричной форме можно записать в виде:

AX=B, (2)

где Х - вектор неизвестных усилий в стержнях и опорных связях, В - вектор проекций внешних нагрузок на узлы, А - матрица системы.

Для того, чтобы система (2) была замкнутой, необходимо чтобы число уравнений 2∙ n_узл совпадало с числом неизвестных, т.е. выполнялось условие (1).

Если количество стержней в ферме будет больше, чем требуется согласно (1), то ферма будет статически неопределимой, если меньше - то геометрически изменяемой.

При этом, важно отметить, что условие (1) является необходимым, но не достаточным для обеспечения геометрической неизменяемости. Как уже упоминалось, кроме обеспечения необходимого числа связей, требуется их правильное размещение.

Рис. 7.19

 

Систему, в которой невозможны взаимные смещения узлов, в предположении, что все стержни абсолютно жесткие, называют жестким диском. В шарнирном треугольнике (например, ABC на рис.7.19) взаимное смещение узлов будет невозможным, следовательно он является жестким диском. Присоединение к такому треугольнику еще одного узла двумя не лежащими на одной прямой связями приведет к образованию системы, в которой также взаимные смещения узлов будут невозможны. Если продолжить этот процесс, то полученная система также будет жестким диском. Примером жесткого диска является простейшая ферма, т.е. ферма, состоящая из шарнирных треугольников (рис.7.19). Взаимные смещения узлов в такой фермы невозможны. Остается только позаботиться о прикреплении полученной простейшей фермы к основанию.

Для того, чтобы обеспечить неподвижность простейшей фермы относительно основания, необходимы как минимум три опорных связи, линии действия которых не параллельны и не пересекаются в одной точке.

Рассмотрим в качестве примера ферму, изображенную на рис.7.1. Очевидно, она относится к простейшим фермам. В ней n_ст =25, n_узл =14, n_оп.св =3. Равенство (1) выполняется: 25=2∙14-3=25. Линии действия трех опорных связей (опорных реакций на рис.7.1) не параллельны и не пересекаются в одной точке, следовательно ферма геометрически неизменяема.

Теперь выполним перестановку опорных связей. Отбросим на левой опоре одну связь, сделав неподвижную опору катковой, но добавим еще одну катковую опору в центре пролета фермы (рис.7.20).

Рис. 7.20

 

В результате, количество опорных связей не изменилось, а осталось равным трем, т.е. равенство (1) осталось справедливым. Однако линии действия опорных связей стали параллельными - направленными вертикально вверх. В результате система получила возможность смещения в горизонтальном направлении, т.е. стала геометрически изменяемой.

Если же в ферме, изображенной на рис.7.1, выполнить перестановку стержней, как показано на рис.7.21, равенство (1) останется неизменным, но система окажется геометрически изменяемой за счет неправильного распределения связей. Это очевидно, т.к. шарнирами C, D, E и F образуется шарнирный квадрат, который при приложении малейшей нагрузки обращается в ромб.

Рис. 7.21

 

Если ферма образована из двух жестких дисков, то для того, чтобы исключить взаимные смещения узлов в полученной системе, необходимо, чтобы они соединялись между собой как минимум тремя связями, линии действия которых не параллельны и не пересекаются в одной точке.

В ферме на рис.7.21 два жестких диска ABCD (он представляет собой простейшую ферму) и FEGH (ферма, образованная из простейшей добавлением одной “лишней” связи) соединяются между собой только двумя связями DF и CE, что и приводит к геометрической изменяемости фермы, в чем мы уже убедились.

Рассмотрим арочную ферму, изображенную на рис.7.12,в. Здесь n_ст =18, n_узл =11, n_оп.св =4. Условие (1) выполняется: 18=11∙2-4=18. Эта ферма также образована двумя жесткими дисками (простейшими фермами). Они соединяются между собой шарниром С, т.е., на первый взгляд, только двумя связями, т.к. шарнир препятствует взаимному смещению соединяемых им узлов в вертикальном и горизонтальном направлениях. Однако, поскольку опоры А и В неподвижны, взаимных горизонтальных смещений точек А и В быть не может. Значит, роль третьей связи играет основание. Поэтому рассматриваемая система геометрически неизменяема, а в обеих опорах возникнут горизонтальные распорные реакции.

Выполним перестановку связей в этой ферме. Сделаем одну из опор катковой, сняв таким образом ограничение на взаимные горизонтальные смещения точек А и В. Однако, добавим стержень, который возьмет на себя роль третьей связи, соединяющей простейшие фермы (рис.7.22). Равенство (1) при этом не нарушится: 19=11∙2-3=19, система останется геометрически неизменяемой, а роль основания по восприятию горизонтального усилия перейдет введенному стержню, работающему в качестве затяжки.

Билет 8

1) Построим линии влияния поперечной силы и изгибающего момента в консольной балке кинематическим способом. Так как левая часть в этой балке неподвижна, то движется только правая часть в положительном направлении. При этом ордината линии влияния момента равна а, ордината линии влияния поперечной силы равна 1.

Для построения линий влияния реакций опор, моментов и попе-

речных сил в двухконсольной балке нужно воспользоваться теми же

условиями равновесия. Отличие будет состоять лишь в том, что груз

при движении переходит и на консоли (рис. 1.5).

Чтобы это учесть, достаточно абсциссу груза х изменить в пре-

делах от 0 до l + d и от 0 до - c при начале координат в опоре А.

Это справедливо для всех линий влияния.

Для сечения 1, расположенного на левой консоли (сила слева от

сечения), получим

М1 = - Р · х = - х.

Если сила справа от сечения, то М1 = 0.

Таким образом, левая ветвь – прямая линия с нулевой ординатой при

х = 0 и ординатой е на конце консоли.

Поперечная сила в сечении 1 при движении груза справа от сече-

ния будет равна Q1 = 0.

Если груз движется слева от сечения, то Q1 = - 1.

В этом случае правая ветвь имеет нулевые ординаты и совпадает с

нулевой линией, а левая ветвь параллельна нулевой линии с ордина-

тами, равными единице.

2) Стержневые системы можно разделить на три группы: плоские; плоскопространственные; пространственные. Рассмотрим только плоские системы. В них все стержни и внешние силы лежат в одной плоскости. К ним относятся: фермы, балки, рамы (рис. 7.1).

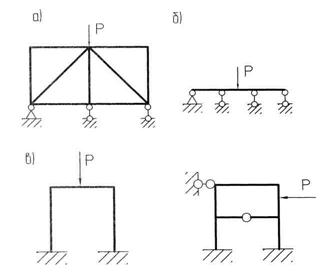
Рис. 7.1

Ферма (рис.7.1, а) — стержневая конструкция, элементы которой работают преимущественно на продольную силу. Нагрузка прикладывается в узлах фермы. Балка — прямой брус, работающий на изгиб (рис. 7.1, б). Рама — стержневая система, элементы которой работают преимущественно на изгиб

Примеры определения степени статической неопределимости.

Ферма ,

где — степень статической неопределимости;

— число стержней, включая и опорные;

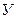— число узлов фермы.

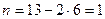. Следовательно, данная ферма один раз статически неопределимая.

Балка ,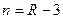

где — число опорных реакций, тогда 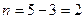, т.е. данная балка два раза статически неопределимая.

Рама ,где — число замкнутых контуров; 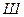— число врезанных шарниров.

Билет 13

1) Кинематический способ построения линий влияния основан на принципе возможных перемещений (принцип Лагранжа). Если система твёрдых тел, связанная между собой идеальными связями, находится в равновесии, то сумма работ всех заданных сил на любых сколь угодно малых возможных перемещениях равна нулю.

Идеальными считаются такие связи, в которых отсутствуют трение, обмятия узлов и другие аналогичные явления. Возможными считаются такие перемещения, какие допускают идеальные связи.

В соответствии с этим методом каждая линия влияния представляет собой эпюру перемещений.

Для построения линии влияния реакции, поперечной силы или изгибающего момента для заданного сечения балки необходимо удалить связь, линию влияния внутреннего усилия для которой требуется построить, и вместо нее ввести требуемое усилие. Таким образом, заданная система станет механизмом с одной степенью свободы. В направлении рассматриваемого внутреннего усилия вводится бесконечно малое перемещение. Направление этого перемещения должно совпадать с внутренним усилием, чтобы оно совершала положительную работу. На базе принципа возможных перемещений записывается уравнение равновесия, из решения которого и определяется требуемое усилие.

2) Рациональной осью трехшарнирной арки заданного пролета и заданной стре-

лы подъема называется такая ось, при которой поперечные сечения арки,

требуемые условиями прочности, будут наименьшими. Уменьшение попереч-

ных размеров связано со снижением действительного напряжения.

Так как нормальные напряжения изгиба обычно превосходят напряжения растяжения-сжатия, то рациональной осью будет такая, при которой изгибающие моменты во всех се- чениях арки будут равны нулю.

во всех сечениях такой арки изгибающий момент равен нулю. Если ось арки и кривая давления определяются соответственно уравнениями

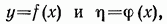
то условием того, что ось арки имеет рациональное очертание, является тождество

 

 

Билет 16

1) Этот способ состоит в том, что мысленно вырезают узлы фермы, прикладывают к ним соответствующие внешние силы и реакции стержней и составляют уравнения равновесия сил, приложенных к каждому узлу. Так как в начале расчета фермы неизвестно, какие стержни фермы растянуты и какие сжаты, то условно предполагают, что все стержни растянуты (реакции стержней направлены от узлов).

Если в результате вычислений получают ответ со знаком «минус», то соответствующий стержень сжат.

Найденные реакции стержней равны по модулю внутренним усилиям в стержнях.

Последовательность рассмотрения узлов обычно определяется условием, что число неизвестных сил, приложенных к узлу, не должно превышать числа уравнений равновесия сил (двух для плоской фермы и трех для пространственной). Тогда эти неизвестные определяются сразу из уравнений равновесия сил, действующих на этот узел.

Если ферма плоская, то можно проверить правильность вычислений, построив многоугольники сил, приложенных к ее узлам. Эти многоугольники должны быть замкнутыми.

Усилия в отдельных стержнях загруженной фермы могут оказаться равными нулю. Такие стержни принято называть нулевыми. Рассмотрим леммы, пользуясь которыми можно определить нулевые стержни плоской фермы, не производя ее расчета.

Рис. 1.9. К лемме 1

Лемма 1. Если в незагруженном узле плоской фермы сходятся два стержня, то усилия в этих стержнях равны нулю (рис. 1.9):

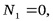
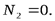
Рис. 1.10. К лемме 2

Лемма 2. Если в незагруженном узле плоской фермы сходятся три стержня, из которых два расположены на одной прямой, то усилие в третьем стержне равно нулю. Усилия в первых двух стержнях равны между собой (рис.1.10).

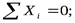
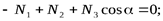
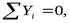
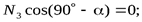
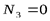и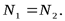

Рис. 1.11. К лемме 3

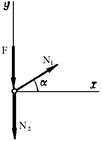
Лемма 3. Если в узле плоской фермы сходятся два стержня и к узлу приложена внешняя сила, линия действия которой совпадает с осью одного из стержней, то усилие в этом стержне равно по модулю приложенной силе, а усилие в другом стержне равно нулю (рис. 1.11):

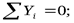
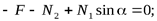
Признаки определения нулевых стержней:

1. Если к узлу с двумя стержнями, не лежащими, на одной прямой, не приложена внешняя нагрузка, то усилия в них равны нулю (рис. 1.2,а);

2. Если в узле сходятся три стержня, две из которых лежат на одной прямой и нагрузка в узле отсутствует, то в третьем стержне, расположенном под углом к этой прямой, усилие равно нулю (рис.1.2,б);

3. Если в узле сходятся два стержня, а нагрузка направлена вдоль оси одного из них, то усилие на другой равен нулю

2) Любую геометрически неизменяемую часть системы назовем диском.

Правило 1: узел присоединяется к диску двумя связями, не лежащими на одной прямой (рис. 3.1).

Правило 2: диск соединяется с другим диском тремя связями, не пересекающимися в одной точке и не параллельными друг другу

Правило 3: три диска соединяются друг с другом тремя шарнирами, не лежащими на одной прямой

Задача кинематического анализа и состоит в том, чтобы определить геометрически изменяема или неизменяема данная система. Он проводимого в два этапа. Вначале определяется степень статической неопределимости конструкции, т. е. наличие или отсутствие лишних внешних или внутренних связей. Затем проводится собственно кинематический анализ образования (создания) конструкции, который заключается в исследовании взаимного расположения элементов конструкции (дисков) и соединяющих их связей.

Число степеней свободы для плоской стержневой системы рассчитывается по формуле, называемой основной формулой кинематического анализа:

 

W = 3Д – 2Ш – С₀.

 

Диск (Д) – неизменяемая часть конструкции, представляющая собой жесткий неподвижный элемент;

Шарнир (Ш) – связь, позволяющая соединяемым ею дискам поворачиваться друг относительно друга;

Опорный стержень (С₀) – число реакций, которые могут возникать во всех связях

При расчете по основной формуле кинематического анализа возможны следующие результаты:

1) W>0 – такая система является геометрически изменяемой и такая конструкция не может служить в качестве инженерного сооружения;

2) W=0 –в схеме введено необходимое число связей и если они введены верно, то система неизменяема и статически определима;

3) W<0 – в системе присутствуют избыточные связи если они введены верно, то система неизменяема и статически неопределима.

 

 

Билет 22

1) При определении внутренних усилий в стержнях фермы применяются следующие методы:

1) Метод моментной точки;

2) Метод проекций;

3) Метод вырезания узлов.

Первые два метод применяются, если можно рассечь ферму на две отдельные части. Сечение должно рассечь не более трех стержней, один из которых и является стержнем, в котором требуется найти внутреннее усилие.

Если при этом два стержня, внутренние усилия в которых не требуется знать, соединяются в одной точке – метод моментной точки; если параллельны друг другу – метод проекций.

В методе вырезания узлов вначале вырезается узел, в котором пересекаются не более двух стержней с неизвестными усилиями, и далее последовательно вырезая узлы достигают требуемого стержня. При этом в каждом из вырезаемых узлов должно пересекаться не более двух неизвестных стержней с неизвестными усилиями.

При расчете усилий в фермах примем следующие условные обозначения: усилия в стержнях верхнего пояса фермы обозначим буквой О, в стержнях нижнего пояса – U, в раскосах – D, в стойках – V. В качестве индексов у этих обозначений применяются цифры, обозначающие узлы фермы, расположенные на концах рассматриваемого стержня.

 

Линия влияния строятся от подвижной силы Р=1, которая перемещается по всей длине фермы.

 

2) Порядок

· строится поэтажная схема балки;

• груз F = 1 помещается на ту балку, где расположено сечение, и линия влияния усилия строится как в однопролётной балке, без учёта всех остальных балок;
• груз F = 1 движется вначале по балкам нижнего этажа, затем поднимается на верхние этажи, то есть линии влияния строятся снизу вверх;
• при движении груза F = 1 по балкам верхних этажей, усилия на нижние не передаются, то есть линии влияния на нижележащих относительно сечения балках нулевые, линии влияния строятся как при узловой передачи нагрузки;
• когда F = 1 находится на опорах, усилия R, M, Q равны нулю. В месте расположения шарнира на линии влияния усилия наблюдается перелом, на консоль линия влияния продолжается под тем же углом наклона оси, что и основная.

Алгоритм построения линии влияния при узловой передаче нагрузки:

1) Строится линия влияния как для обычной простой балки;

2) На построенной линии влияния ординаты под узлами панели, имеющей сечение, для которого строится линия влияния, соединяются прямой линией (передаточной прямой ).

 

При построении линий влияния для многопролетных балок расчет начинается с балки, которой принадлежит рассматриваемое сечение, а затем переходят к остальным элементам многопролетной балки, причем усилия от единичной нагрузки могут передаваться с основных балок на вспомогательные. На вспомогательных балках линия влияния строится как при узловой передаче нагрузки. Т.е. для многопролетных балок вначале строится линия влияния для балки, в которой находится рассматриваемое сечение, а затем построенная линия влияния продолжается для всех балок вспомогательных к балке с сечением (для вспомогательных линия влияния проводится через ноль на нейтральной оси под шарнирными опорами).

 

Билет 24

1) Потенциальной будем называть такой вид энергии, который накапливается в теле при его упругих деформациях. При нагружении стержня внешними силами часть потенциальной энергии действующего на стержень груза полностью переходит в потенциальную энергию деформации стержня.

Согласно закону сохранения энергии, работа внешних сил не исчезает, а переходит в потенциальную энергию (V), накапливаемую в упругом теле при его деформировании.

Следовательно, потенциальная энергия деформации численно равна работе внешних сил при нагружении тела (или работе внутренних сил, совершаемой ими в процессе разгружения).

Таким образом, потенциальная энергия деформации стержня, испытывающего, например, растяжение, кручение и прямой поперечный изгиб, равна:

.

Как видно из этой формулы, потенциальная энергия деформации всегда положительна, поскольку она является квадратичной функцией обобщенных сил (или обобщенных перемещений, так как последние линейно связаны с обобщенными силами). Отсюда следует, что потенциальная энергия, накопленная в результате действия группы сил, не равна сумме потенциальных энергий, накопленных от действия каждой нагрузки в отдельности. То есть принцип независимости действия сил при вычислении потенциальной энергии деформации не применим.

Внешние силы, приложенные к упругому телу и вызывающие изменение геометрии тела, совершают работу А на соответству­ющих перемещениях. Одновременно с этим в упругом теле накап­ливается потенциальная энергия его деформирования U. При дей­ствии динамических внешних нагрузок часть работы внешних сил превращается в кинетическую энергию движения частиц тела К. Приняв энергетическое состояние системы до момента действия данных сил равным нулю, и в условиях отсутствия рассеивания энергии, уравнение баланса энергии можно записать в следующем виде:

А = U + K. (2.8)

При действии статических нагрузок К = 0, следовательно,

А = U. (2.9)

Это означает, что при статическом нагружении работа внешних сил полностью преобразуется в потенциальную энергию деформа­ции. При разгрузке тела производится работа за счет потенциаль­ной энергии деформации, накопленной телом. Таким образом, уп­ругое тело является аккумулятором энергии.

2) Увеличить высоты фермы можно за счет введения в состав каждой панели дополнительных двухопорных ферм – шпренгелей, опирающихся на шарниры основной фермы. Стержни шпренгелей работают лишь на местную нагрузку, т.е. на нагрузку, приложенную в пределах их пролетов.

В принципе шпренгельные фермы рассчитываются так – заданную ферму нужно расчленить на две схемы:

а) на основную ферму;

б) на шпренгельные элементы, которые условно рассматриваются как треугольные фермы, опирающиеся на узлы основной фермы.

Удалить шпренгельные элементы. Всю нагрузку перенести в узлы основной фермы. Эту схему рассчитываем отдельно.

Отдельно выделяем треугольные шпренгеля и загружаем их своей местной нагрузкой Р. Их также рассчитывают отдельно.

Для определения усилий в стержнях заданной фермы необходимо сделать следующее - треугольные шпренгельные фермы мысленно наложить на схему основной фермы, т.е. наложить схему II на схему I. А затем поступать так:

а) в тех стержнях, которые при наложении не совпадают друг с другом, усилия принимать непосредственно по результатам раздельных расчетов этих схем.

б) в тех стержнях, которые при наложении схем совпадают, усилия необходимо определять как алгебраическую сумму усилий из расчетов обоих схе

В зависимости от их расположения в ферме различают одноярусные и двухярусные шпренгели.

Среди элементов фермы, содержащей в своем составе одноярусные шпренгели, выделяют следующие виды:

1) элементы, входящие в состав только основной ферме. Внутренние усилия в таких элементах рассчитывают рассматривая только основную ферму, при этом шпренгели не рассматривают.

2) элементы, входящие в состав только шпренгелей. Внутренние усилия в таких элементах рассчитывают рассматривая только шпренгель, при этом шпренгель рассчитывают как отдельную ферму, имеющую свои опоры.

3) элементы, входящие в состав основной фермы и шпренгеля. Внутренние усилия в таких элементах рассчитывают, суммируя усилия в элементе основной фермы и в шпренгеле.

Среди элементов фермы, содержащей в своем составе одноярусные шпренгели, выделяют следующие виды:

1) элементы, входящие в состав только основной ферме. Внутренние усилия в таких элементах рассчитывают рассматривая только основную ферму, при этом шпренгели не рассматривают.

2) элементы, входяющие в состав только шпренгелей. Внутренние усилия в таких элементах рассчитывают рассматривая только шпренгель, при этом шпренгель рассчитывают как отдельную ферму, имеющую свои опоры.

3) элементы, входящие в состав основной фермы и шпренгеля. Внутренние усилия в таких элементах рассчитывают, суммируя усилия в элементе основной фермы и в шпренгеле;

4) элементы, входящие в состав основной фермы, линии влияния для которых строятся по разному в случаях когда сила Р=1 перемещается по нижнему и верхнему поясам.

 

Билет 28

1) Метод сил. Здесь в качестве неизвестных рассматриваются усилия – силы и моменты.

При расчете по методу сил основными искомыми величи­нами являются усилия в лишних связях. Знание усилий в лишних связях позволит по методу сечений выполнять полный расчет по определению усилий, возникающих в поперечных сечениях элементов заданной системы.

Алгоритм расчета методом сил

Независимо от особенностей рассматриваемой конструкции, можно выделить следующую последовательность расчета статически неопределимых систем методом сил:

1. Определить степень статической неопределимости.

2. Выбрать основную систему.

3. Сформировать эквивалентную систему.

4. Записать систему канонических уравнений.

5. Построить единичные и грузовые эпюры внутренних силовых факторов, возникающих в элементах рассматриваемой конструкции.

6. Вычислить коэффициенты при неизвестных и свободные члены системы канонических уравнений.

7. Построить суммарную единичную эпюру.

 

Основная проблема СНС – это наличие лишних связей, что наделяет эти системы особыми свойствами, рассмотренными выше. С точки зрения расчета, эти связи не позволяют решить задачу на основе уравнений равновесия и метода сечений. Необходимо, как известно, составить еще и n дополнительных уравнений на основе условий совместности деформаций (перемещений).

В методе сил за известное принимают реакции в лишних опорных связях и (или) внутренние усилия, соответствующие лишним внутренним связям. Эти неизвестные с целью упрощения разрешающих уравнений обозначают: , где n=R-U – степень статической неопределимости, равная числу избыточных связей. Для плоских рам эта величина определяется по формуле:

K- число замкнутых контуров;

U_ш – число простых шарнирных узлов, включая шарнирно-неподвижные опоры;

U_n – число подвижных узлов, включая шарниро-подвижные опоры

Выбор основной системы

Система, освобожденная от дополнительных связей, становится статически определимой. Она носит название основной систе­мы. После того как дополнительные связи отброшены и система превращена в статически определимую, необходимо ввести вместо связей неизвестные силовые факторы, которые принято называть лишними неизвестными. В тех сечениях, где запрещены линейные перемещения, вводятся силы. Там, где запрещены угловые смещения, вводятся моменты. Как в том, так и в другом случае неизвестные силовые факторы будем обозначать X _i, где i — номер неизвестного. Наибольшее значение i равно степени статической неопределимости системы. Заметим, что для внутренних связей силы X _i, — являются взаимными. Если в каком-либо сечении рама разрезана, то равные и противоположные друг другу силы и моменты прикладываются как к правой, так и к левой частям системы.

Основную систему с приложенными к ней лишними неизвестными Х ₁, Х ₂,... X _n и внешней нагрузкой Р называют эквивалентной системой при условии, что её действительные перемещения согласуются с наложенными на исходную систему связями. Для каждой статически неопределимой заданной системы (рис. 10, а) можно подобрать, как правило, различные основные системы (рис. 10, б, в), однако их должно объединять следующее условие - основная система должна быть статически определимой и геометрически неизменяемой (т.е. не должна менять свою гео­метрию без деформаций элементов).

2) Перед расчетом статически неопределимой конструкции необходимо сначала определить степень статической неопределимости рассматриваемойсистемы. Для балок и простых рам степень статической неопределимости равна числу лишних опорных связей. В каждой связи возникает опорная реакция, поэтому степень статической неопределимости можно найти, сосчитав разность между количеством неизвестных опорных реакций и числом независимых уравнений статики.

Определение реакций в дополнительных связях называют рас­крытием статической неопределимости. Выполняется оно по единому алгоритму, который состоит из следующих шагов.

1. Определение степени статической неопределимости.

2. Выбор основной системы (ОС).

3. Переход к эквивалентной системе (ЭС).

4. Составление системы канонических уравнений.

5. Вычисление коэффициентов при неизвестных и свободных чле­нов уравнений. Решение системы канонических уравнений.

6. Построение суммарных эпюр внутренних силовых факторов.

7. Проверка правильности раскры­тия статической неопределимости.

Степень статической неопределимости внешне статически неопределимой системы S легко установить путем вычитания из общего числа опорных стержней m количество независимых урав­нений равновесия n, которое может быть составлено для данной системы (одно - для одномерных; три - для плоских и шесть - для пространственных систем).

где C - число связей, накладываемых на конструкцию; У - число возможных независимых уравнений равновесия, которые можно составить для рассматриваемой системы.

Для плоской рамы, изображенной на рис.5, учитывая, что защемление эквивалентно трем опорным стержням, получаем:

C = 3 + 2 2 +1 = 8; n = C - У = 8-3 = 5,

т.е. данная система 5 раз статически неопределима.

Степень свободы при внешней статической неопределимости определяется по формуле:

W =2 Ш + С ₀-3 Д,

где Д – число жестких дисков, из которых состоит стержневая система;

Ш – число простых шарниров, соединяющих между собой жесткие диски. Если шарнир соединяет более двух дисков, то он называется кратным и равен d-1 простым шарнирам(d – число соединяемых дисков);

С_о – число опорных стержней, наложенных на систему.

Основная система метода сил получится путем удаления в заданной раме четырех «лишних» связей. Рассмотрим несколько возможных вариантов основных систем. Так как заданная рама упруго симметрична то будем выбирать только симметричные схемы вариантов основных систем, соблюдая основные требов