1. Сформировать структуру замкнутой системы, состоящей из идеального интегратора и двух апериодических звеньев первого порядка с постоянными времени  ,
,  ,
, 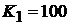 . Общий коэффициент усиления разомкнутой САУ равен 100.
. Общий коэффициент усиления разомкнутой САУ равен 100.
Ввести главную обратную связь и параллельную корректирующую цепь с  . Выполнить анализ характеристик замкнутой системы.
. Выполнить анализ характеристик замкнутой системы.
Сохранить структуру в файле и скопировать ее для дальнейших модификаций.
2. В режиме "Частотный синтез" проанализировать логарифмические частотные характеристики исходной системы. Сформировать желаемую ЛАЧХ с частотой единичного усиления около 1 рад/с, при несовпадении высокочастотных участков желаемой и исходной ЛАЧХ. В этом случае желаемая ЛАЧХ строится в направлении слева направо, т.е. с включением форсирующих и апериодических звеньев.
Записать полученную передаточную функцию в модель системы. Произвести расчет переходного процесса в скорректированной замкнутой системе. Проверить выполнение условий физической реализуемости корректирующей цепи (все коэффициенты полиномов числителя и знаменателя передаточной функции должны соответствовать отрицательной обратной связи).
3. Повторить синтез корректора, обеспечив совпадение желаемой ЛЧХ с высокочастотной частью ЛЧХ исходной системы. В этом случае желаемая ЛАЧХ строится в направлении справа налево. Корректор при этом состоит из набора пропорционально интегрирующих и инерционно дифференцирующих звеньев.
Записать полученную передаточную функцию в модель системы. Произвести расчет переходного процесса в скорректированной системе. Проверить выполнение условий физической реализуемости корректирующей цепи.
4. Изменить структуру системы, охватив корректирующей цепью только апериодический усилитель.
Выполнить синтез корректора и записать полученную передаточную функцию в модель системы. Произвести расчет переходного процесса в скорректированной замкнутой системе.
5. Изменить структуру системы, охватив корректирующей цепью интегратор.
Выполнить синтез корректора и записать полученную передаточную функцию в модель системы. Произвести расчет переходного процесса в скорректированной замкнутой системе.
6. Исследовать упрощенный вариант коррекции. Для структурной схемы САУ, сформированной в п.1, осуществить коррекцию гибкой инерционной отрицательной обратной связью по ускорению. Передаточную функцию корректора задать в виде  . Не используя режим частотного синтеза, подобрать параметры
. Не используя режим частотного синтеза, подобрать параметры  и
и  корректора, обеспечивающие апериодический или близкий к нему характер переходного процесса. Произвести расчет переходного процесса в скорректированной замкнутой системе. Оценить качество переходного процесса.
корректора, обеспечивающие апериодический или близкий к нему характер переходного процесса. Произвести расчет переходного процесса в скорректированной замкнутой системе. Оценить качество переходного процесса.
Повторить коррекцию для варианта обратной связи с более крутым переходом к среднечастотной области, приняв передаточную функцию корректора  .
.
Сравнить передаточные функции упрощенного варианта корректора с результатами частотного синтеза (пункт 3).
Содержание отчета
Графики переходных процессов.
Передаточные функции и ЛЧХ корректирующих устройств.
Передаточные функции и ЛЧХ исходных и скорректированных систем.
Значения характерных частот.
Выводы по результатам коррекции.
ЛАБОРАТОРНАЯ РАБОТА №7
ИССЛЕДОВАНИЕ ХАРАКТЕРИСТИК ТИПОВЫХ ЗВЕНЬЕВ ЦИФРОВЫХ САУ
Большинство сигналов, подлежащих обработке в автоматических системах, являются непрерывными. Однако при достаточно высокой частоте дискретизации и точности аналого-цифрового преобразователя (АЦП) замена непрерывного сигнала его цифровым эквивалентом дает целый ряд преимуществ. Прежде всего, надо отметить стабильность и повторяемость при производстве характеристик цифровых устройств. Важны также гибкость и простота модификации параметров системы за счет программной реализации алгоритмов.
Рассмотрим характеристики цифровой системы без цепи главной обратной связи, т.е. разомкнутой САУ.
Основные погрешности, возникающие при переходе к цифровой обработке, связаны с дискретизацией по времени, квантованием сигнала при аналого-цифровом преобразовании и округлением при вычислениях и обратном (цифроаналоговом) преобразовании.
Дискретизация по времени происходит с частотой дискретизации  , где
, где  - интервал дискретизации. Частота дискретизации в соответствии с теоремой отсчетов [Л.4] должна не менее чем в два раза превосходить верхнюю граничную частоту
- интервал дискретизации. Частота дискретизации в соответствии с теоремой отсчетов [Л.4] должна не менее чем в два раза превосходить верхнюю граничную частоту  спектра непрерывного сигнала. Выбор
спектра непрерывного сигнала. Выбор  нетривиален, поскольку точное восстановление сигнала по его выборкам требует применения идеального фильтра нижних частот (ФНЧ). На практике восстановление аналогового сигнала выполняет цифроаналоговый преобразователь (ЦАП). Ступенчатая экстраполяция в конце интервала дискретизации дает большую ошибку, поэтому
нетривиален, поскольку точное восстановление сигнала по его выборкам требует применения идеального фильтра нижних частот (ФНЧ). На практике восстановление аналогового сигнала выполняет цифроаналоговый преобразователь (ЦАП). Ступенчатая экстраполяция в конце интервала дискретизации дает большую ошибку, поэтому  приходится увеличивать примерно в 50 раз. Заметим, что переход к линейной экстраполяции
приходится увеличивать примерно в 50 раз. Заметим, что переход к линейной экстраполяции  улучшает точность восстановления на порядок. Перед дискретизацией для уменьшения ошибки от эффекта наложения спектров [Л.4] необходимо ограничить спектра сигнала выше частоты
улучшает точность восстановления на порядок. Перед дискретизацией для уменьшения ошибки от эффекта наложения спектров [Л.4] необходимо ограничить спектра сигнала выше частоты  .
.
Аналого-цифровое преобразование приводит к появлению шумов квантования, дисперсия которых ( ) зависит от разрядности АЦП и его опорного напряжения (
) зависит от разрядности АЦП и его опорного напряжения (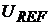 ). Для
). Для  -разрядного АЦП дискрет шкалы составляет
-разрядного АЦП дискрет шкалы составляет  , дисперсия
, дисперсия  , а среднеквадратическое отклонение
, а среднеквадратическое отклонение  .
.
Математическое описание цифровых систем базируется на аппарате разностных уравнений и 
 преобразовании [Л.4]. Разностные уравнения получают из дифференциального уравнения заменой функций их значениями в моменты дискретизации
преобразовании [Л.4]. Разностные уравнения получают из дифференциального уравнения заменой функций их значениями в моменты дискретизации  , а производных – нормированными к интервалу
, а производных – нормированными к интервалу  конечными разностями. Обычно используют обратные (нисходящие) разности
конечными разностями. Обычно используют обратные (нисходящие) разности  , т.к. предшествующие значения функции известны. Заметим, что в системах программного управления будущие значения функций известны заранее. В этом случае можно использовать прямые (восходящие) разности
, т.к. предшествующие значения функции известны. Заметим, что в системах программного управления будущие значения функций известны заранее. В этом случае можно использовать прямые (восходящие) разности  . Любое типовое звено линейной системы может быть с определенной погрешностью представлено эквивалентным цифровым фильтром, алгоритм работы которого в общем виде описывается разностным уравнением:
. Любое типовое звено линейной системы может быть с определенной погрешностью представлено эквивалентным цифровым фильтром, алгоритм работы которого в общем виде описывается разностным уравнением:
 , (4)
, (4)
где  – входной, а
– входной, а 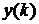 – выходной сигналы в k -тый дискретный момент времени. Аналогом передаточной функции служит системная функция цифрового фильтра
– выходной сигналы в k -тый дискретный момент времени. Аналогом передаточной функции служит системная функция цифрового фильтра  , где через
, где через 
 обозначены
обозначены  преобразования последовательностей
преобразования последовательностей  и
и 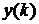 . Взяв
. Взяв  преобразование от обеих частей разностного уравнения (4), получим
преобразование от обеих частей разностного уравнения (4), получим  . Системная функция примет вид:
. Системная функция примет вид:
 . (5) Подстановкой в (5)
. (5) Подстановкой в (5)  получаем периодическую зависимость от частоты
получаем периодическую зависимость от частоты  . Выделив из нее модуль и аргумент, можно получить периодические АЧХ и ФЧХ. Более удобно строить частотные характеристики с использованием т.н.абсолютной псевдочастоты
. Выделив из нее модуль и аргумент, можно получить периодические АЧХ и ФЧХ. Более удобно строить частотные характеристики с использованием т.н.абсолютной псевдочастоты  [Л.2]. Псевдочастота
[Л.2]. Псевдочастота  при малых частотах
при малых частотах  практически совпадает с обычной частотой
практически совпадает с обычной частотой  что удобно при анализе низкочастотной части характеристик, определяющей точность САУ. Для получения АЧХ и ФЧХ достаточно воспользоваться подстановкой в системную функцию
что удобно при анализе низкочастотной части характеристик, определяющей точность САУ. Для получения АЧХ и ФЧХ достаточно воспользоваться подстановкой в системную функцию  .
.
Системные функции ЦФ, выполняющих дифференцирование и интегрирование получим непосредственно из соотношения  . Рассмотрим два полезных варианта разложения логарифмической функции в ряд:
. Рассмотрим два полезных варианта разложения логарифмической функции в ряд:
 ,
,  . (7)
. (7)
Отсюда вытекает третий вариант ряда:  . Устойчивый алгоритм дифференцирования соответствует применению оператора на основе обратных разностей. Принимая
. Устойчивый алгоритм дифференцирования соответствует применению оператора на основе обратных разностей. Принимая  , получим:
, получим:
 (8)
(8)
Условие сходимости ряда (8)  позволяет определить максимальную частоту в спектре дифференцируемого процесса
позволяет определить максимальную частоту в спектре дифференцируемого процесса  . Методическая погрешность операции дифференцирования при ограничении числа суммируемых членов ряда (8) можно оценить по величине старшего отбрасываемого члена. Важно отметить, что с ростом длины импульсной характеристики [Л.5] возрастает дисперсия шумов квантования. Таким образом, существует оптимум, зависящий от разрядности АЦП.
. Методическая погрешность операции дифференцирования при ограничении числа суммируемых членов ряда (8) можно оценить по величине старшего отбрасываемого члена. Важно отметить, что с ростом длины импульсной характеристики [Л.5] возрастает дисперсия шумов квантования. Таким образом, существует оптимум, зависящий от разрядности АЦП.
Простейший алгоритм вычисления первой и второй производных  и
и  , соответственно. Системные функции имеют вид
, соответственно. Системные функции имеют вид  и
и  .
.
Алгоритм цифрового интегрирования можно получить путем реализации оператора интегрирования 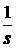 . Простейшие системные функции соответствуют приближению логарифма одним членом разложения в ряд. Ниже приведенные варианты дают устойчивые алгоритмы, соответствующие интегрированию по методу:
. Простейшие системные функции соответствуют приближению логарифма одним членом разложения в ряд. Ниже приведенные варианты дают устойчивые алгоритмы, соответствующие интегрированию по методу:
прямоугольников с недостатком  ,
, 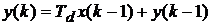 ;
;
прямоугольников с избытком  ,
, 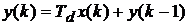 ;
;
трапеций  ,
,  .
.
Сравним частотные характеристики интеграторов с использованием псевдочастоты. Например, для интегратора с системной функцией  , где
, где  получим
получим 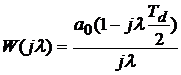 . Сравнение с непрерывным аналогом
. Сравнение с непрерывным аналогом  показывает почти полную их идентичность, однако множитель в числителе лает дополнительное фазовое запаздывание. Заметим, что более сложные алгоритмы интегрирования в автоматике не применяют. Как показано в [Л.5], все три основных алгоритма дают нулевую установившуюся ошибку при постоянном воздействии. Метод трапеций не дает ошибки и при линейном воздействии.
показывает почти полную их идентичность, однако множитель в числителе лает дополнительное фазовое запаздывание. Заметим, что более сложные алгоритмы интегрирования в автоматике не применяют. Как показано в [Л.5], все три основных алгоритма дают нулевую установившуюся ошибку при постоянном воздействии. Метод трапеций не дает ошибки и при линейном воздействии.
Цифровой интегратор любого типа имеет импульсную характеристику бесконечной длины, что сопровождается накоплением дисперсии шумов квантования.
В лабораторной работе исследуются типовые звенья САУ, реализованные в виде подпрограмм, написанных на языке ассемблер семейства микроЭВМ MCS 51.
Для обеспечения визуального наблюдения выходных сигналов САУ используется восьмиразрядный цифроаналоговый преобразователь. Указанное обстоятельство накладывает ряд ограничений на допустимый диапазон входных сигналов и внутренних переменных (0…255) в моделирующих программах. За нулевой уровень принят код 128, соответствующий половине опорного напряжения ЦАП.
Программу цифровой фильтрации для моделирования типовых звеньев можно сделать универсальной, однако при этом из-за неэффективно расходуемого времени процессора существенно возрастает задержка вывода сигналов в ЦАП. По этой причине в лабораторной работе использован набор простых подпрограмм, каждая из которых моделирует соответствующее типовое звено.
Частота дискретизации сигналов задается таймером Т0. Таймер запрограммирован в режим 1 (шестнадцатиразрядный счетчик) и вырабатывает сигналы прерывания с периодом кратным 250 мкс, что соответствует программируемому интервалу дискретизации  . Значение N (кратность) задается во внутреннем ОЗУ в ячейке с адресом 32 h.
. Значение N (кратность) задается во внутреннем ОЗУ в ячейке с адресом 32 h.
Типовые звенья цифровых САУ представлены следующими подпрограммами:
APZ 1 – апериодическое звено первого порядка;
INTР – интегрирующее звено по методу прямоугольников;
INTТ – интегрирующее звено по методу трапеций;
INTРI – пропорционально-интегрирующее звено;
FRZ – форсирующее звено.
APZ 1.
Системная функция имеет вид:
 , где
, где  ,
, 
Для работы подпрограммы требуется задать приближенное значение 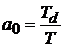 и
и 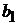 .
.
Алгоритм цифровой фильтрации  реализуется подпрограммой APZ 1.
реализуется подпрограммой APZ 1.
INTP.
Системная функция описывается выражением: 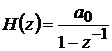 , где
, где  . Алгоритм цифровой фильтрации
. Алгоритм цифровой фильтрации  реализуется подпрограммой INTР.
реализуется подпрограммой INTР.
INTT.
Системная функция  , где
, где 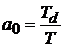 . Алгоритм цифровой фильтрации
. Алгоритм цифровой фильтрации  реализуется подпрограммой INTT.
реализуется подпрограммой INTT.
INTPI.
Системная функция пропорционально-интегрирующего звена имеет вид:  , где
, где  ,
,  – коэффициент пропорциональности, равный
– коэффициент пропорциональности, равный  .
.
Алгоритм цифровой фильтрации определяется выражением  и реализуется подпрограммой INTРI
и реализуется подпрограммой INTРI
FRZ.
Системная функция представлена в виде:  , где
, где  . Алгоритм цифровой фильтрации
. Алгоритм цифровой фильтрации  использует только один коэффициент
использует только один коэффициент  и реализуется подпрограммой FRZ.
и реализуется подпрограммой FRZ.