Для ПСМ разработаны четкие правила, определяющие процесс движения симплекса и область оптимума.
Правило 1. Основное правило, определяющее движение симплекса к оптимуму, можно назвать правилом отражения.
Оно состоит в том, что вершина симплекса, имеющая "наихудшее" значение параметра оптимизации, отбрасывается. Рассчитываются координаты новой вершины, которая является зеркальным отражением старой вершины относительно сохраняемой грани.
Пусть "наихудшее" значение параметра оптимизации наблюдается в вершине q1
симплекса q1Л1М1. Отбросив вершину q1, 
строят новый симплекс q2Л1М1, в котором вершина q2 является зеркальным отражением вершины q1 относительно грани Л1М1.
Применяя правило отражения к симплексу q2Л1М1, можно построить следующий симплекс. Отбрасывая "худшие" вершины симплекса, осуществляют движение к оптимуму.
Координаты новой вершины симплекса можно рассчитать по формуле:
 (1)
(1)
где
 – координаты новой вершины;
– координаты новой вершины;
j=1,2,…,q –номер фактора;
i =1,2,…(q+I) – номер вершины симплекса;
 -координаты отброшенной «наихудшей» вершины.
-координаты отброшенной «наихудшей» вершины.
Правило 2. Если число факторов больше трех, рекомендуется повторять опыты примерно через 2(q+I) шагов. Применение этого правила связано с тем, что при наличии большого числа факторов информация может оказаться устарелой вследствие дрейфов. В результате этого отклики, входящие в один и тот же симплекс, становятся несопоставимыми.
Правило 3. Cистема симплексов может вращаться относительно «наилучшей» вершины. Признаком вращения является сохранение одной и той же вершины на протяжении q+I и более шагов (рис.5.)
При обнаружении вращения необходимо повторить опыт в «наилучшей» вершине еще раз. Если первоначально зафиксированное наблюдение в этой вершине было ложным, то маловероятно, что повторно сделанный опыт дал столь же хороший результат. В этом случае вершине присваивается результат второго опыта и «наилучшая» вершина отбрасывается. Если же повторное наблюдение совпало с первоначальным, то «наилучшая» вершина симплекса находится вблизи оптимума. После анализа поверхности отклика можно сделать заключение о конце движения. 
Правило 4. При отбрасывании одной или нескольких вершин симплекса, в новых вершинах отклики могут оказаться более худшими, чем в отбрасываемых вершинах. Тогда при отбрасывании этих новых вершин полученный симплекс переходит в старый симплекс. Возникает колебание. Такое явление вполне возможно, если:
· некоторым вершинам симплекса присвоены ложные результаты опытов;
· q вершин симплекса находятся вблизи оптимума или на «гребне» холма, а q+I вершина - у «подошвы» (рис 6.а);
· одна из вершин находится вблизи или на «гребне» холма, а q вершин у «подошвы» (рис 6.б);
Например, исследователь, отбрасывая «наихудшую» вершину Л1 симплекса q1 Л2 М1 (рис. 6а), строит вершину Л2. Однако, вершина Л2, входящая в симплекс q1 Л2 М1, имеет также наихудшее значение и подлежит отбрасыванию. Отбрасывая вершину Л2, исследователь получает вершину Л1. На рис.6.б показан аналогичный случай, когда отбрасываются две вершины одновременно М1 и q1 в симплексе q1 Л2 М1.
Если отбрасывается одна вершина, то рекомендуется для успешного продвижения вперед вернуться к первоначальному симплексу 
и отбросить наихудшую вершину, не считая самой наихудшей.
Формулы отражения справедливы для расчета переменных, записанных как в кодированной, так и в натуральной форме.
Оценка ситуации с достижением области оптимума
О достижении области оптимума можно судить по следующим признакам:
Возникновение вращения симплексов относительно вершин имеющей наилучшее значение параметра оптимизации.
Достижение теоретически возможного значения параметра оптимизации во всех вершинах симплекса.
При планировании экспериментов оценку ситуации о достижении области оптимума, как правило, определяют по совокупности нескольких признаков.
Достоинства и недостатки последовательного симплексного метода
Метод ПСМ неоднократно сравнивался с различными другими методами, применяемыми для поиска оптимальных технологических условий, например, с очень распространенным среди исследователей методом Бокса-Уилсона.
Было отмечено, что ПСМ обладает большей адаптивностью, чем метод Бокса-Уилсона, причем последний требует почти в два раза больше опытов. Однако по точности отыскания оптимума ПСМ немного уступает методу Бокса-Уилсона.
ПСМ обладает целым рядом преимуществ по сравнению с другими методами планирования:
1. ПСМ исключительно прост. Здесь не требуется проводить статистический анализ экспериментальных данных.
2. Во многих химических процессах оптимум имеет тенденции дрейфовать во времени. (изменение свойств катализатора, свойств исходных компонентов и т.д.). ПСМ позволяет непрерывно следить за дрейфующей точкой оптимума.
3. При изучении технологических процессов на переменные факторы, как правило, накладываются ограничения. ПСМ позволяет производить планирование и при этих условиях. Если расчет показывает, что новая вершина попадает в полупустую область, т.е. нарушит ограничения на факторы, то опыт в этой вершине не проводится. Отражается вторая "наихудшая" вершина, т.е. применяют правило 4.
4. ПСМ можно использовать при наличии многомерного параметра оптимизации.
5. Можно указать и на другие преимущества ПСМ: полная формализация движения симплексов к оптимуму, возможность увеличения переменных в процессе экспериментирования, возрастание эффективности ПСМ с увеличением числа переменных и т.д.
ПСМ имеет следующие недостатки:
1. ПСМ дает ограниченную информацию о поверхности отклика.
2. Эффективность движения резко снижается (больше ошибочных движений) при приближении к области оптимума.
Для оперативных расчетов с использованием ПСМ необходимо разработать компьютерную программу, позволяющую автоматизировать процедуру всех необходимых расчетов.
Пример использования ПСМ для оптимизации ХТС
Постановка задачи:
Изучался процесс получения нового вещества. Входные параметры: температура процесса (х1) и давление (х2) в реакторе.
Пределы изменения температуры: 0-100 С.
Пределы изменения давления: 0-10 атм.
Выходной параметр (y) –выход реакции измеряется в процентах. Пределы изменения выходного параметра 0-100%. Необходимо найти максимальное значение выходного параметра (параметра оптимизации).
Заменим реальный процесс, реализуемый на физической системе, т.е. на ХТС, графической системой, - зависимостью выходного параметра (y) от входных параметров х1.х2. Изобразим процесс в виде изолиний.
Изолинии (линии равного уровня) - это некоторые замкнутые кривые, не пересекающиеся друг с другом. Каждая изолиния имеет какое-то значение.
Будем также считать, что изучаемый процесс имеет только один экстремум – максимум или минимум. Для изучаемой задачи это максимум, значение которого равно 100%. Для изображения графической системы лучше всего использовать миллиметровку.
Например, такая система может иметь следующий вид (см. Рис. 1).
Решение задачи
На первом этап е необходимо задать стандартную матрицу планирования для двух факторов. Используем для этого почти целочисленную матрицу планирования.
Такая матрица имеет вид:
Табл1
| Вершина | x1 код | x2код | y |
| A | -1,73 | -1,73 | |
| B | -1 | ||
| C | -1 |
Эта матрица записана в кодированной (безразмерной форме) и не привязана к сформулированной задаче.
На втором этапе необходимо пересчитать заданную матрицу из кодированной в натуральную (размерную) форму.
Для пересчета переменных используют следующую формулу:
 (2)
(2)
где
Xj - натуральное значение j фактора;
 - базовое значение j фактора в натуральной форме;
- базовое значение j фактора в натуральной форме;
 – кодированное значение j фактора;
– кодированное значение j фактора;
 - интервал варьирования j фактора (натуральная форма).
- интервал варьирования j фактора (натуральная форма).
Данную формулу применяют для каждого j фактора. Для этого для каждого j фактора выбирают X0 –базовый уровень и интервал варьирования ΔX. Все данные сводят в таблицу2.
Таблица 2.
| Обозначение фактора: | температура | давление |
| X0 | ||
| ΔX |
За базовую точку X0 обычно берут наилучшую точку, которую обнаруживают при предварительном проведении опытов. Возьмем для данной задачи следующую базовую точку: Х1=25; Х2=2
Интервал варьирования ΔX определяет размеры симплекса в натуральной форме. Обычно интервал варьирования равен 0,1-0,2 от интервала варьирования фактора (cм. таблицу). Интервал варьирования для каждого фактора равен:
ΔХ1=25; Δ Х2=2
Итак, план эксперимента в натуральной форме имеет вид:
| Вершина | Кодированная форма | Натуральная форма | Y | ||
| x1 | x2 | Х1 | Х2 | ||
| A | -1,73 | -1,73 | 7,679 | 0,267 | |
| B | -1 | ||||
| C | -1 |
Вершины симплекса отобразим на рисунке 1 и получим симплекс ABC. Сразу отметим, что координаты вершин симплекса не должны быть отрицательными и выходить за заданные границы изменения факторов.
На третьем этапе в вершинах симплекса проводят эксперименты (поскольку реальный объект отсутствует, то значения параметра оптимизации (y) берут с диаграммы изолиний т.е. рис1.) и вносят в столбец Y. Значение Y снимают с графика приближенно, например, вершине С соответствует значение 30, вершине В соответствует значение 34, а вершине А соответствует значение 17.
На четвертом этапе сравнивают полученные значения Y между собой и выбирают вершину, в которой значение опыта наихудшее (в данной задаче – наименьшее). Итак, наихудшая вершина – А. Следовательно, необходимо рассчитать координаты новой вершины – А1. Расчет можно вести, используя натуральные значения факторов. Используя формулу (1) рассчитаем две координаты:
Для Х1
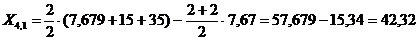

Итак, координаты новой вершины А1: X1=42,32 и Х2=3,73 отметим эту точку на графике.
На пятом этапе проводят опыт в новой вершине –А1 и полученное значение заносят в таблицу (это значение равно 47), а затем сравнивают со значением в вершине А. Если в рассчитанной вершине А1 значение параметра оптимизации больше, чем в старой А, то вершину А отбрасывают (зачеркивают строку в таблице с вершиной А.). Итак, получен новый симплекс А1ВС, который переместился в пространстве в сторону экстремума.
| Вершина | Кодированная форма | Натуральная форма | Y | ||
| x1 | x2 | Х1 | Х2 | ||
| A | -1,73 | -1,73 | 7,679 | 0,267 | |
| B | -1 | ||||
| C | -1 | ||||
| А1 | 42,32 | 3,73 | |||
Далее переходят к четвертому этапу.
Очевидно нужно отбросить вершину С, тогда координаты новой вершины С1 равны:
Х1=22,3 Х2=5,7
Значение параметра оптимизации в вершине С1 равно 36.Это значение больше чем в вершине С, следовательно, шаг сделан успешно. Вершину С отбрасывают. Итак, получен симплекс А1ВС1.
| Вершина | Кодированная форма | Натуральная форма | Y | ||
| x1 | x2 | Х1 | Х2 | ||
| A | -1,73 | -1,73 | 7,679 | 0,267 | |
| B | -1 | ||||
| C | -1 | ||||
| А1 | 42,32 | 3,73 | |||
| С1 | 22,3 | 5,7 |
Далее переходят к этапу 4.
Решение задачи продолжают до тех пор, пока в вершинах симплекса увеличивается значение параметра оптимизации.
Задание:
Необходимо придумать аналогичную двухфакторную задачу.
Нужно нарисовать изолинии, составить матрицу планирования в кодированной и натуральной формах и осуществить движение в область максимума, либо в область минимума.
Желательно составить программу в Excel для расчета координат новой вершине симплекса, а также таблицу движения симплекса. На графике изобразить схему движения симплекса.