Министерство образования и науки Российской Федерации
Федеральное государственное автономное образовательное
Учреждение высшего образования
«Санкт-Петербургский политехнический университет Петра Великого»
Университетский политехнический колледж
Методические рекомендации по организации внеаудиторной самостоятельной работы по математике для студентов заочного отделения
38.02.01 «Экономика и бухгалтерский учет»
1 курс
2017г.
| РАССМОТРЕНЫ: предметной (цикловой) комиссией математики Протокол № ____ от «______ » ____________ 2016 г. Председатель ПЦК Е.В. Кудрявцева ___________________________ подпись | УТВЕРЖДАЮ: Зам. Директора по УР М.Г.Рождественская ____________ «___»______________2016 г. |
| Рекомендованы Методическим советом УПК СПбПУ Протокол №___ от «___» __________2016 г. Старший методист О.М. Симонова Зам. Директора по УМР Е.Г. Конакина ___________________ подпись |
Методические рекомендации по организации внеаудиторной самостоятельной работы студентов заочного отделения разработаны на основе Федеральных государственных образовательных стандартов (далее – ФГОС) по специальности среднего профессионального образования (далее - СПО) 38.02.01 «Экономика и бухгалтерский учет» и учебных планов Университетского политехнического колледжа федерального государственного автономного образовательного учреждения высшего образования «Санкт-Петербургский политехнический университет Петра Великого»
Разработчик: Е. В. Кудрявцева, преподаватель УПК СПбПУ
Пояснительная записка
Методические указания к выполнению внеаудиторной самостоятельной работы студентов заочного отделения по дисциплине «Математика» предназначены для студентов по специальности 38.02.01 «Экономика и бухгалтерский учет»соответствуютФедеральным образовательным государственным стандартам.
Цель методических указаний: оказание помощи студентам в организации неаудиторной самостоятельной работы по математике.
Заочная форма обучения предполагает самостоятельную работу студента над учебным материалом: поиск, анализ и оценка информации по содержанию учебного материала, решение задач, выполнение контрольных заданий. Студент должен изучить соответствующие разделы курса Математика, используя учебные издания, интернет-ресурсы, дополнительную литературу. В случае возникновения затруднений при самостоятельном изучении материала, студент может обратиться к преподавателю для получения устной консультации.
Знания приобретаются студентами в процессе проведения занятий и в процессе самоподготовки.
Умения формируются при выполнении практических работ.
Настоящие методические указания содержат список литературы, требования к результатам освоения дисциплины «Математика», справочные материалы, которые позволят студентам самостоятельно овладеть знаниями, умениями и навыками по дисциплине «Математика», опытом творческой и исследовательской деятельности и направлены на формирование общих и профессиональных компетенций:
Требования к результатам освоения дисциплины:
Обучающийся должен уметь:
- Решать прикладные задачи в области профессиональной деятельности;
Обучающийся должен знать:
- значение математики в профессиональной деятельности и при освоении ППССЗ;
- основные математические методы решения прикладных задач в области профессиональной деятельности;
- основные понятия и методы математического анализа, дискретной математики, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики;
- основы интегрального и дифференциального исчисления.
Цели самостоятельной внеаудиторной работы студентов:
- закрепление, углубление, расширение и систематизация знаний,
- самостоятельное овладение новым учебным материалом;
- формирование профессиональных явлений;
- формирование умений и навыков самостоятельного умственного труда;
- мотивирование регулярной целенаправленной работы по освоению специальности;
- развитие самостоятельного мышления;
- формирование убежденности, волевых черт характера, способности к самоорганизации.
Основные виды самостоятельной работы студентов по дисциплине «Математика»:
1. Первичное овладение знаниями (усвоение нового материала):
- чтение дополнительной литературы;
- составление плана текста, конспектирование прочитанного;
- решение примеров и задач.
2. Закрепление и систематизация знаний:
- работа с конспектами лекций;
- решение примеров и задач;
- ответы на контрольные вопросы.
3. Применение знаний, формирование умений:
- решение примеров и задач по образцу, вариативных задач
- решение контрольных работ.
Требования к оформлению конспекта:
Конспект– это краткое изложение или краткая запись содержания.
Требования к конспекту: системность, логичность изложения, краткость, убедительность и доказательность.
Этапы конспектирования:
1. Прочитайте текст, отметьте в нем новые слова, непонятные места, имена, даты, перечислите основные мысли текста, составьте план.
2. Выясните значение новых непонятных слов и символов.
3. Вторичное чтение сочетайте с записями основных мыслей. Запись ведите своими словами, не переписывайте текст дословно.
Правила записи текста
1. Запись должна быть компактной.
2. В тексте необходимо применять выделения и разграничения: подчеркивание (для выделения заголовка и подзаголовка, выводов, отделения одной темы от другой, одного вопроса от другого);
- красную строку для обозначения абзацев и пунктов плана;
- нумерацию абзацев;
- выделение с помощью рамки определений, правил, законов, формул и так далее.
3. При записи допускается пользоваться сокращениями.
4. Сформулируйте и запишите вывод.
Перечень тем для самостоятельного изучения
(С указанием источников):
1) Основные понятия теории множеств
2) Формулы логики
3) Обыкновенные дифференциальные уравнения
Богомолов Н.В. Практические занятия по математике 2014 г. Глава 15, & 1, 3, 4, 5
4) Основы теории вероятностей и математической статистики
Богомолов Н.В. Практические занятия по математике 2014 г. Глава 16, & 1-6
5) Элементы линейной алгебры
Дмитрий Письменный. Конспект лекций по высшей математике,
часть 1, глава 1, & 1, 2, 3, 4
6) Основы теории комплексных чисел
Богомолов Н.В. Практические занятия по математике 2014 г. Глава 14, & 1-4
Справочные материалы:
Основные понятия комбинаторики. Задачи, при решении которых приходится составлять различные комбинации из конечного числа элементов и производить подсчет числа всех возможных таких комбинаций, называются комбинаторными.
Этот раздел математики находит широкое практическое применение во многих вопросах естествознания и техники.
Размещения. Пусть имеется множество, содержащее n элементов. Каждое его упорядоченное подмножество, содержащее m элементов, называется размещением из n элементов по m элементов.
Из определения вытекает, что 0≤m≤n и что размещения из n элементов по m – это все m-элементные подмножества, отличающиеся составом элементов или порядком их следования.
Число размещений из n элементов по m элементов в каждом обозначают  и вычисляют по формуле
и вычисляют по формуле

Число размещений из n элементов по m элементов в каждом равно произведению m последовательно убывающих натуральных чисел, из которых большее есть n! (n-факториал).

Условились считать, что 0!=1.
Тогда формулу числа размещений из n элементов по m элементов можно записать в другом виде:

Пример 1. Сколькими способами из группы, включающей 25 участников, можно выбрать актив группы в составе старосты, комсорга и профорга.
Решение. Состав актива группы является упорядоченным множеством из 25 элементов по три элемента. Значит, искомое число способов равно числу размещения из 25 элементов по три элемента в каждом:

Или 
Пример 2. Перед выпуском группа в 30 человек обменялась фотокарточками. Сколько было всего роздано фотокарточек?
Решение. Передача фотокарточек одним учащимся другому есть размещение из 30 элементов по два элемента. Искомое число фотокарточек равно числу размещений из 30 элементов по два элемента в каждом:

Перестановки. Резмещения из n элементов по n элементов называют перестановками из n элементов.
Из определения следует, что перестановки являются частным случаем размещений. Так как каждая перестановка содержит все n элементов множнства, то различные перестановки отличаются друг от друга только порядком элементов.
Число перестановок из n элементов данного множества обозначают  и вычисляют по формуле
и вычисляют по формуле

Пример 3. Сколько четырехзначных чисел можно составить из цифр 1, 2, 3, 4 без повторений?
Решение. По условию дано множество из четырех элементов, которые требуется расположить в определенном порядке. Значит, требуется найти количество перестановок из четырех элементов:

Т.е. из цифр 1, 2, 3, 4 можно составить 24 четырехзначных числа (без повторений цифр).
Пример 4. Сколькими способами можно рассадить 10 гостей по десяти местам за праздничным столом?
Решение. Искомое число способов равно числу перестановок из 10 элементов:

Сочетания. Пусть имеется множество, состоящее из n элементов. Каждое его подмножество, содержащее m элементов, называется сочетанием сочетанием из n элементов по m элементов.
Таким образом, сочетания из n элементов по m элементов – это все m-элементные подмножества n-элементного множества, причем различными подмножествами считаются только те, которые имеют неодинаковый состав элементов.
Подмножества, отличающиеся друг от друга порядком следования элементов, не считаются различными.
Число подмножеств по m элементов в каждом, содержащихся во множестве из n элементов, т.е. число сочетаний из n элементов по m элементов в каждом, обозначают  и вычисляют по формуле
и вычисляют по формуле

Число сочетаний  обладает следующим свойством:
обладает следующим свойством:

Так

Пример 5. Сколько всего игр должны провести 20 футбольных команд в однокруговом чемпионате?
Решение. Так как игра любой команды А с командой В совпадает с любой игрой команды В с командой А, то каждая игра есть сочетание из 20 элементов по 2. Искомое число всех игр равно числу сочетаний из 20 элементов по 2. Искомое число всех игр равно числу сочетаний из 20 элементов по 2 элемента в каждом:

Комплексные числа.
Основные понятия и определения: Решение многих задач сводиться к решению алгебраических уравнений. Поэтому исследование алгебраических уравнений является одним из важнейших вопросов математики. Стремление сделать уравнение разрешимым – одна из главных причин расширения понятия числа.
Однако действительных чисел недостаточно для того, чтобы решить любое алгебраическое уравнение. Например, уравнение  не имеет действительных корней. Поэтому приходиться расширять множество действительных чисел до нового множества, такого, чтобы в этом множестве уравнения вида
не имеет действительных корней. Поэтому приходиться расширять множество действительных чисел до нового множества, такого, чтобы в этом множестве уравнения вида
 имели решения.
имели решения.
Корень уравнения  или
или  называется мнимой единицей и обозначается буквой i.
называется мнимой единицей и обозначается буквой i.
Таким образом, символ i удовлетворяет условию  .
.
Комплексным числом называется выражение вида  , где a и b - действительные числа, а i – мнимая единица.
, где a и b - действительные числа, а i – мнимая единица.
Числа a называется действительной частью комплексного числа, а число bi – мнимой частью.
Комплексное число часто обозначают буквой z.
Множество комплексных чисел принято обозначать буквой C.
Запись комплексного числа в виде  называется алгебраической формой записи комплексного числа.
называется алгебраической формой записи комплексного числа.
Два комплексных числа  называются равными тогда и только тогда, когда
называются равными тогда и только тогда, когда  т.е. когда равны их действительные части и коэффициенты при мнимой части.
т.е. когда равны их действительные части и коэффициенты при мнимой части.
Понятие  для комплексных чисел не определяются.
для комплексных чисел не определяются.
Комплексное число  называется нулем и обозначается 0; комплексное число
называется нулем и обозначается 0; комплексное число
 отождествляется с действительным числом a, т.е.
отождествляется с действительным числом a, т.е. 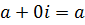 ; комплексное число
; комплексное число  называется чисто мнимым и обозначается bi, т.е.
называется чисто мнимым и обозначается bi, т.е.  .
.
Число 0 является единственным числом, которое одновременно и действительное, и чисто мнимое.
Комплексные числа  называются сопряженными.
называются сопряженными.
Действия над комплексными числами в алгебраической форме. Суммой двух комплексных чисел  называется комплексное число
называется комплексное число

Произведением двух комплексных чисел  называется комплексное число
называется комплексное число 
Вычитание комплексных чисел вводиться как операция, обратная сложению; деление комплексных чисел вводиться как операция, обратная умножению.
Правила вычитания и деления комплексных чисел  определяются формулами
определяются формулами


Где 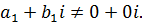
Формулы, определяющие правила действий над комплексными числами в алгебраической форме, не нуждаются в запоминании.
Формулы суммы, разности и произведения комплексных чисел получаются автоматически, если формально выполнить соответствующие действия над двучленами  и заменить
и заменить  .
.
При делении на комплексное число достаточно умножить числитель и знаменатель дроби  на число, сопряженное знаменателю, т.е. на
на число, сопряженное знаменателю, т.е. на  .
.
Возведение комплексного числа в степень производится по формулам возведения двучлена в степень, но при этом надо учитывать что:
 ,
,
 ,
,
 ,
,
 ,
,




Например, 
Пример 1. Найти сумму и произведение комлексных чисел  =3+5i.
=3+5i.
Решение. Сумму находим формальным сложением двучленов  :
:
 +
+  =
= 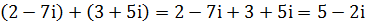
Произведение находим формальным перемножением двучленов  с последующей заменой
с последующей заменой  на -1
на -1

Пример 2. Даны комплексные числа 
Решение. Разность находим формальным вычитанием двучленов 10 

Что бы найти частное  умножим числитель и знаменатель этой дроби на число, сопряжение знаменателю
умножим числитель и знаменатель этой дроби на число, сопряжение знаменателю 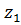 :
:
 =
= 
Пример 3. Найти комплексное число  .
.
Решение. Выполнив в знаменателе дроби возведение в степень, получим

Умножив числитель и знаменатель полученной дроби на число, сопряженное знаменателю, т. е на  , получим
, получим