Выполнил:
Гармаев Арсалан
Проверил:
Д.ф.-м.н., профессор Булатов М.В.
Улан-Удэ
Содержание
1. Глобальный анализ ошибки...............................................................................................3
2. Результаты локальной сверхсходимости для нелинейных Вольтерра
2-го рода………………………………………………4
3. ИУВ типа Гаммерштейна: неявно линейная коллокация ……………………………………………………………...5
4. Список литературы…………………………………………………..12
1. Глобальный анализ ошибки
Ошибка коллокации 
= 
– 
для решения коллокации ∈ 
К общим нелинейным интегральных уравнений Вольтерра(ИУВ)
удовлетворяет, по 
Поскольку 
, мы можем записать это в виде
при условии, что 
непрерывна и ограничена. Функции 
являются аргументами, возникающими в условиях остатка Тейлора. Следовательно, с использованием локального представление ошибки коллокации , доказательство теоремы Результаты глобальной конвергенции(2.2.3) легко распространяется на нелинейные ИУВ, и в частности версия Гаммерштейна часто встречается в приложениях.
Оставляя подробности читателю, мы просто заявляем, что при соответствующих предположениях о существовании и регулярности, решение коллокации 
индуцирует ошибку, порядок которой описывается формулой
и это справедливо для любого 
c 
2. Результаты локальной сверхсходимости для нелинейных Вольтерра 2-го рода
Для нелинейных ИУВ при достаточно регулярных решений глобальных и локальных результатов суперсходимости теорем 2.2.5 и 2.2.6 остаются действительными. Это не удивительно, потому что если мы применим теорему Тейлора с квадратичным остатком, мы можем записать уравнение для ошибки коллокации,
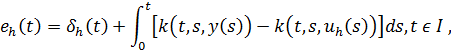
Где 
в форме
Вместе с 
и
Здесь,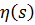 
:=y(t)- 
для некоторых 
с 0 < < 1. Мы выводим из
порядка глобальной сходимости , что
при условии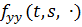 
ограничено на D x 
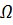для некоторых 
. Обозначение ядра повторного растворителя, связанного с ядром 
по 
решение линеаризованного уравнения ошибки можно записать в виде
Следовательно, утверждения о достижимом порядке 
по 
следуют из знакомых квадратурных аргументов, основанных на степени точности интерполяционных квадратурных формул с точками коллокации как абсциссы. Другими словами, результаты суперсходимости теорем 2.2.5 и 2.2.6 остаются справедливо для нелинейных ИУВ.
3.ИУВ типа Гаммерштейна: неявно линейная коллокация
Мы видели в конце раздела 2.1.5 что интеграл Вольтерра–Гаммерштейна имеет уравнение
Вместе
Может быть переписана в форме, которая приводит к более привлекательной для вычислений версии метода коллокации. Эта форма основана на ператоре Niemytzki (или:оператор замещения) N,
Что позволяет переработать (2.3.2) как «неявно линейный» уравнение интеграла Вольтерра,
с линейным оператором Вольтерра
Решение исходного ИУВ (2.3.2), затем получается итерация путем
Теперь мы приближаем z на решение коллокации 
И определить приближение 
к решению y исходного ИУВ посредством
Вычислительная форма уравнения коллокации (2.3.6) на 
использует локальное представление
И, таким образом, определяется
(2.3.9)
(i = 1,..., m), с термином задержки
После того как 
было найдено, мы получим приближение к решению y уравнения учитывая ИУВ (2.3.2) на 
на
В приложениях ядро K (t, s) обычно имеет тип свертки, K (t, s) =k (t - s), где функция памяти k часто такова, что возникающие интегралы из
Можно найти аналитически, избегая при этом квадратурных приближений. Более важным преимуществом неявно линейной коллокации является то, что, отличие от прямого коллокации для (2.3.2), интегралы не нужно переучитывать для каждого этапа итерации при решении нелинейной
алгебраической системы (2.3.9), Или при вычислении приближения 
для разных значений t ∈ I по формуле (2.3.10).
Замечание Неявно линейные методы коллокации (называемые «новый тип коллокации методы») были впервые введены для интегральных уравнений Фредгольма в Кумаре и Слоане (1987) и Кумар (1987); см. также Бруннер (1991, 1992), Франкель (1995) и Канеко, Норен и Падилья (1997)
Оказывается, аппроксимация , полученная неявно линейной коллокацией и итерационное решение коллокации 
, порожденная «прямой» коллокацией тесно связаны и для некоторых ядер по существу идентичны. Таким образом, для разумного выбранные параметры коллокации оба подхода дают суперсходимость приближения одних и тех же глобальных и локальных порядков. Это уточняется в следующая теорема.
Теорема 2.3.1. Предположим, что:
(a) Данные функции g, K и G в (2.3.2) непрерывны на своих областях, и G таково, что VHIE обладает единственным решением y ∈ C (I).
(б) - приближение к решению y Вольтерра-Гаммерштейна уравнение (2.3.2), полученное неявно линейной коллокацией и определяемое формулой (2.3.6), (2.3.7).
(в) 
Обозначает дискретизированное итерационное решение коллокации, соответствующее «Прямое» решение коллокации 
∈ 
определяемый полностью дискретизированным (2.3.11) ниже, используя те же коллокационные точки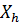 
, как и для вычисления ∈ в (2.3.6).
Тогда
для всех 
Доказательство. Если мы решим заданное уравнение Вольтерра-Гаммерштейна (2.3.2) на «прямой», Коллокации, то точное уравнение коллокации
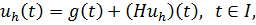
И точное итерационное решение коллокации найдено из
Для 
) и 
эти уравнения становятся, соответственно,
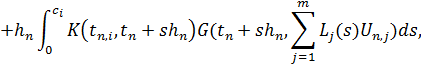
И
Здесь, мы установили
Рассмотрим теперь их полностью дискретизированные версии, основанные на интерполяционной m -точке квадратурных формул произведения с весовой функцией K (·, s) и абсцисс По точкам коллокации: согласно разделу 2.2.3 они даются выражением
И
(2.3.12)
Допустим 
Из (2.3.11) и (2.3.12) получаем, таким образом, уравнения
(2.3.13)
И
(2.3.14)
Мы хотим показать, что 
где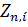 
Определяются решением нелинейной алгебраической системы (2.3.9). Это легко проверить по индукции, используя очевидный факт, что утверждение
Верно для n=0. Остальные детали этого простого доказательства мы оставляем читателю.
В отношении приложений ядро обычно имеет тип свертки, 
И, следовательно, квадратурные веса в (2.3.11) - (2.3.14) имею аналогичную структуру, например.
Для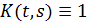 
мы получаем результат теоремы 1.1.9 для специального уравнения Вольтерра- Интегральное уравнение Гаммерштейна, возникающее в интегральной форме начального значения проблема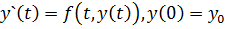 
Список использованной литературы
1) Александрова Н. В. История математических терминов, понятий, обозначений: Словарь-справочник. М.: Изд-во ЛКИ, 2008, 248 с.
2)Бруннер Г. Методы коллокации для интеграла Вольтерры и связанные с ними функциональные уравнения,2004,612 с.
3)Булатов М.В. Численное решение системы уравнений Вольтерры первого вида, 1998,585-589с.
4)Булатов М.В. и В.Ф. Чистякова. Численный метод решения дифференциально-алгебраических уравнений,2002, 439-449с.